Fungsi komposisi dan invers merupakan konsep penting dalam matematika yang banyak diaplikasikan dalam berbagai bidang. Fungsi komposisi melibatkan penyusunan dua fungsi atau lebih, sedangkan fungsi invers membalikkan suatu fungsi.
Memahami cara menentukan dan menggunakan fungsi komposisi dan invers sangat penting untuk menyelesaikan masalah matematika yang kompleks. Dalam artikel ini, kita akan mengeksplorasi konsep-konsep ini melalui contoh soal dan langkah-langkah penyelesaian yang jelas.
Pengertian Fungsi Komposisi dan Invers
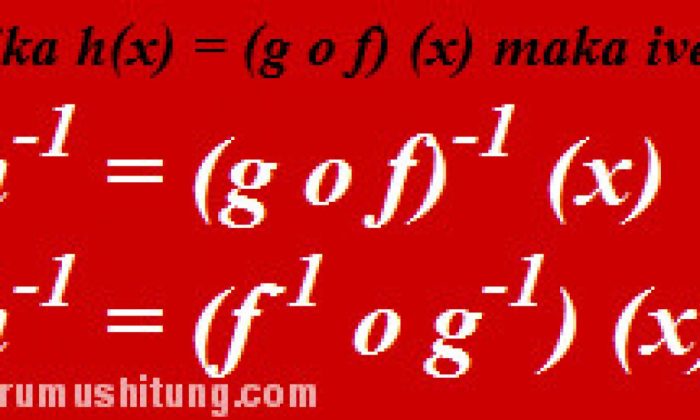
Dalam matematika, fungsi memainkan peran penting dalam memodelkan hubungan antara dua variabel. Dua operasi penting yang dilakukan pada fungsi adalah komposisi fungsi dan invers fungsi. Konsep-konsep ini sangat penting untuk memahami berbagai aplikasi matematika, termasuk aljabar, kalkulus, dan analisis.
Fungsi Komposisi
Fungsi komposisi, dilambangkan dengan f∘g (dibaca “f komposisi g”), adalah fungsi baru yang diperoleh dengan menerapkan fungsi f ke output fungsi g. Secara matematis, untuk dua fungsi f dan g dengan domain dan kodomain yang sesuai, fungsi komposisi f∘g didefinisikan sebagai:
(f∘g)(x) = f(g(x))
Dengan kata lain, untuk setiap nilai x dalam domain g, kita terlebih dahulu mengevaluasi g(x) dan kemudian mengevaluasi f(g(x)).
Fungsi Invers
Fungsi invers, dilambangkan dengan f -1 (dibaca “f invers”), adalah fungsi baru yang membatalkan fungsi f. Secara matematis, untuk suatu fungsi f yang memiliki invers, f -1 didefinisikan sebagai:
f -1 (f(x)) = xdanf(f -1 (x)) = x
Dengan kata lain, fungsi invers membalikkan hubungan yang ditentukan oleh fungsi f. Jika f memetakan x ke y, maka f -1 memetakan y kembali ke x.
Cara Menentukan Fungsi Komposisi

Menentukan fungsi komposisi melibatkan menggabungkan dua fungsi untuk membentuk fungsi baru. Berikut langkah-langkah untuk menentukan fungsi komposisi:
Langkah-langkah Menentukan Fungsi Komposisi
- Tentukan dua fungsi: Misalkan f(x) dan g(x).
- Ganti variabel masukan fungsi dalam: Ganti variabel masukan f(x) dengan g(x).
- Sederhanakan: Sederhanakan fungsi baru yang dihasilkan.
Contoh
Misalkan kita memiliki fungsi f(x) = x + 2 dan g(x) = x 2 . Fungsi komposisi f o g (dibaca “f komposisi g”) didefinisikan sebagai:
f o g(x) = f(g(x)) = f(x 2 ) = x 2 + 2
Cara Menentukan Fungsi Invers
Fungsi invers adalah fungsi yang membalikkan fungsi asli. Untuk menentukan fungsi invers, kita dapat mengikuti langkah-langkah berikut:
Langkah-langkah Menentukan Fungsi Invers
- Tukar variabel input dan output dalam fungsi asli.
- Selesaikan persamaan yang dihasilkan untuk variabel input baru.
- Fungsi invers adalah fungsi baru yang diperoleh dengan mengganti variabel input asli dengan variabel input baru.
Tabel Proses Penentuan Fungsi Invers
| Langkah | Deskripsi ||—|—|| 1 | Tukar x dan y dalam f(x). || 2 | Selesaikan y untuk x. || 3 | Ganti x dengan f -1 (x) untuk mendapatkan fungsi invers. |
Contoh Soal dan Pembahasan
Untuk memahami konsep fungsi komposisi dan invers, mari kita bahas beberapa contoh soal berikut:
Contoh Soal Fungsi Komposisi
- Diketahui fungsi f(x) = x^2 + 1 dan g(x) = x
– 2. Tentukan fungsi komposisi (f ∘ g)(x) dan (g ∘ f)(x).
Langkah-langkah Penyelesaian:
- (f ∘ g)(x) = f(g(x)) = f(x
- 2) = (x
- 2)^2 + 1
- (g ∘ f)(x) = g(f(x)) = g(x^2 + 1) = (x^2 + 1)
- 2 = x^2
- 1
Contoh Soal Fungsi Invers
- Tentukan invers dari fungsi f(x) = 2x + 1.
Langkah-langkah Penyelesaian:
- Tukar variabel x dan y: y = 2x + 1
- Selesaikan y untuk x: x = (y
1) / 2
1) / 2
Manfaat Mempelajari Fungsi Komposisi dan Invers

Mempelajari fungsi komposisi dan invers sangat penting dalam matematika karena memberikan berbagai manfaat, di antaranya:
Manfaat Mempelajari Fungsi Komposisi
- Memahami cara menggabungkan fungsi untuk membuat fungsi baru.
- Menyederhanakan ekspresi matematika yang kompleks.
- Menganalisis sifat fungsi komposisi, seperti domain dan range.
Manfaat Mempelajari Fungsi Invers
- Memahami cara membalikkan fungsi untuk memecahkan persamaan.
- Menemukan fungsi invers dari fungsi trigonometri dan fungsi eksponensial.
- Menganalisis sifat fungsi invers, seperti invertibilitas dan kekontinuan.
Ringkasan Akhir

Menguasai fungsi komposisi dan invers sangat bermanfaat untuk memecahkan masalah matematika, memahami struktur fungsi, dan mengembangkan keterampilan berpikir kritis. Dengan memahami konsep-konsep ini, kita dapat memperoleh wawasan yang lebih dalam tentang hubungan antar fungsi dan mengaplikasikannya dalam berbagai bidang, seperti aljabar, kalkulus, dan fisika.
Pertanyaan Umum (FAQ)
Apa perbedaan antara fungsi komposisi dan invers?
Fungsi komposisi menggabungkan dua fungsi, sedangkan fungsi invers membalikkan suatu fungsi.
Bagaimana cara menentukan fungsi komposisi?
Masukkan fungsi kedua ke dalam fungsi pertama, menggantikan variabel masukan dengan keluaran dari fungsi kedua.
Apa saja manfaat mempelajari fungsi komposisi dan invers?
Membantu memecahkan masalah matematika yang kompleks, memahami struktur fungsi, dan mengembangkan keterampilan berpikir kritis.
