Dalam dunia geometri, lingkaran memegang peran penting sebagai salah satu bangun datar dasar. Pemahaman yang mendalam tentang konsep lingkaran sangat penting bagi siswa kelas 6 untuk mengembangkan keterampilan pemecahan masalah yang kuat. Artikel ini akan membahas berbagai aspek soal cerita lingkaran, mulai dari konsep dasar hingga teknik penyelesaian yang efektif.

Lingkaran didefinisikan sebagai kumpulan semua titik pada bidang yang berjarak sama dari titik tetap yang disebut pusat. Jarak dari titik mana pun pada lingkaran ke pusatnya disebut jari-jari, sedangkan diameter adalah jarak antara dua titik pada lingkaran yang melalui pusatnya.

Pengertian Lingkaran

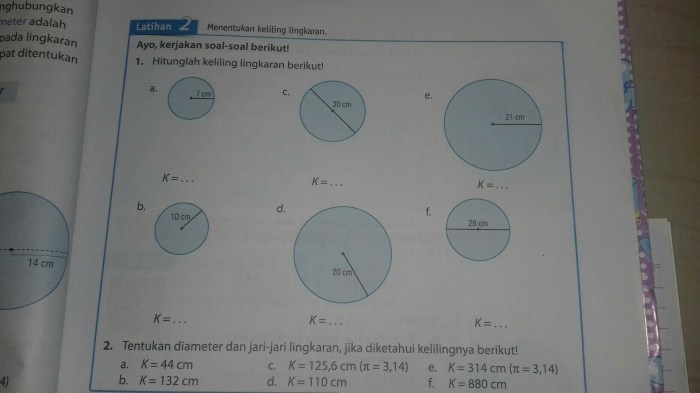
Lingkaran adalah sebuah bentuk geometri datar yang dibatasi oleh kurva tertutup yang disebut keliling. Setiap titik pada keliling lingkaran berjarak sama dari sebuah titik tetap yang disebut pusat lingkaran.

Rumus Keliling dan Luas Lingkaran

*

*Keliling Lingkaran (K)

K = 2πr

di mana:

K adalah keliling lingkaran

π adalah konstanta matematika sekitar 3,14

r adalah jari-jari lingkaran (jarak dari pusat ke keliling)

*

*Luas Lingkaran (L)

L = πr²

di mana:

L adalah luas lingkaran

π adalah konstanta matematika sekitar 3,14

r adalah jari-jari lingkaran (jarak dari pusat ke keliling)

Sifat-Sifat Lingkaran

Lingkaran adalah bentuk geometri dua dimensi yang terdiri dari semua titik pada bidang yang berjarak sama dari titik tetap yang disebut pusat. Lingkaran memiliki beberapa sifat unik yang membedakannya dari bentuk geometri lainnya.

Definisi Sifat-Sifat Lingkaran

Sifat-sifat lingkaran meliputi:

• Memiliki satu pusat.
• Setiap titik pada lingkaran berjarak sama dari pusat.
• Memiliki keliling.
• Memiliki luas.
• Memiliki jari-jari dan diameter.

Jari-Jari dan Diameter

Jari-jari (r) adalah ruas garis yang menghubungkan pusat lingkaran ke titik mana pun pada lingkaran. Diameter (d) adalah ruas garis yang menghubungkan dua titik pada lingkaran dan melewati pusat. Diameter sama dengan dua kali jari-jari (d = 2r).

Keliling

Keliling lingkaran adalah panjang keseluruhan lingkaran. Keliling dihitung menggunakan rumus K = 2πr, di mana π adalah konstanta matematika sekitar 3,14.

Luas

Luas lingkaran adalah ukuran ruang yang dibatasi oleh lingkaran. Luas dihitung menggunakan rumus L = πr², di mana π adalah konstanta matematika sekitar 3,14.

Jenis-Jenis Lingkaran

Lingkaran dapat diklasifikasikan ke dalam berbagai jenis berdasarkan bentuknya. Masing-masing jenis memiliki karakteristik unik yang membedakannya dari jenis lainnya.

Berikut adalah beberapa jenis lingkaran berdasarkan bentuknya:

Lingkaran Beraturan

Lingkaran beraturan adalah lingkaran yang memiliki bentuk bulat sempurna. Semua titik pada lingkaran beraturan berjarak sama dari titik pusatnya.

Lingkaran Tidak Beraturan

Lingkaran tidak beraturan adalah lingkaran yang bentuknya tidak bulat sempurna. Titik-titik pada lingkaran tidak beraturan berjarak tidak sama dari titik pusatnya.

Elips

Elips adalah lingkaran yang bentuknya lonjong. Elips memiliki dua sumbu, yaitu sumbu mayor dan sumbu minor. Sumbu mayor adalah sumbu terpanjang, sedangkan sumbu minor adalah sumbu terpendek.

Parabola

Parabola adalah lingkaran yang bentuknya seperti huruf U. Parabola memiliki satu titik fokus dan satu sumbu simetri.

Hiperbola

Hiperbola adalah lingkaran yang bentuknya seperti dua kurva yang berpotongan. Hiperbola memiliki dua titik fokus dan dua sumbu simetri.

Permasalahan Soal Lingkaran

Soal lingkaran dalam matematika seringkali melibatkan berbagai permasalahan yang menguji pemahaman konsep dasar dan aplikasi teorema lingkaran. Permasalahan ini dapat diklasifikasikan ke dalam beberapa jenis, antara lain:

Jenis-Jenis Permasalahan Soal Lingkaran

Jenis	Deskripsi	Contoh Soal
Mencari Luas	Menentukan luas lingkaran berdasarkan jari-jari atau diameter yang diberikan.	Hitunglah luas lingkaran dengan jari-jari 7 cm.
Mencari Keliling	Menghitung keliling lingkaran berdasarkan jari-jari atau diameter yang diberikan.	Hitunglah keliling lingkaran dengan diameter 10 cm.
Mencari Jari-jari atau Diameter	Menentukan jari-jari atau diameter lingkaran berdasarkan luas atau keliling yang diketahui.	Suatu lingkaran memiliki keliling 28 cm. Tentukan jari-jari lingkaran tersebut.
Mencari Posisi Titik	Menentukan posisi titik relatif terhadap lingkaran, seperti titik di dalam, di luar, atau pada lingkaran.	Tentukan posisi titik (5, 3) terhadap lingkaran dengan pusat (2, 2) dan jari-jari 4.
Mencari Persamaan Lingkaran	Menentukan persamaan lingkaran berdasarkan pusat dan jari-jarinya.	Tulislah persamaan lingkaran dengan pusat (3, 2) dan jari-jari 5.

Cara Menyelesaikan Soal Lingkaran

Dalam geometri, lingkaran adalah bentuk dua dimensi yang didefinisikan sebagai himpunan semua titik pada bidang yang berjarak sama dari titik tetap yang disebut pusat.

Berikut langkah-langkah untuk menyelesaikan soal lingkaran:

Rumus Lingkaran

• Keliling lingkaran: $K\; =\; 2\backslash pi\; r$
• Luas lingkaran: $L\; =\; \backslash pi\; r^2$

Langkah-langkah Penyelesaian

1. Identifikasi informasi yang diberikan dalam soal, seperti jari-jari ($r$) atau keliling ($K$) atau luas ($L$).
2. Tentukan rumus yang sesuai untuk digunakan, berdasarkan informasi yang diberikan.
3. Substitusikan nilai yang diketahui ke dalam rumus.
4. Hitung hasil akhir menggunakan kalkulator atau secara manual.
5. Verifikasi jawaban dengan memeriksa apakah hasilnya masuk akal dan sesuai dengan konteks soal.

Tips dan Trik

• Hafalkan rumus keliling dan luas lingkaran.
• Gunakan nilai $\backslash pi\; \backslash approx\; 3,14$ untuk perhitungan cepat.
• Untuk soal yang lebih sulit, gunakan teknik aljabar atau trigonometri untuk menyelesaikannya.

Contoh Soal dan Pembahasan

Untuk memperkuat pemahaman mengenai lingkaran, berikut ini beberapa contoh soal dan pembahasannya:

Soal 1

Hitunglah luas dan keliling lingkaran dengan jari-jari 7 cm.

Luas = πr ² = π(7 cm) ² = 153,94 cm ²

Keliling = 2πr = 2π(7 cm) = 43,98 cm

Soal Latihan

Untuk menguji pemahaman tentang lingkaran, dapat dirancang beberapa soal latihan berikut:

Soal 1

Sebuah lingkaran memiliki jari-jari 7 cm. Hitunglah keliling dan luas lingkaran tersebut.

Soal 2

Dua buah lingkaran memiliki jari-jari masing-masing 10 cm dan 15 cm. Tentukan perbandingan luas kedua lingkaran tersebut.

Soal 3

Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Sebuah lingkaran memiliki luas yang sama dengan luas persegi panjang tersebut. Tentukan jari-jari lingkaran.

Kunci Jawaban

1. Keliling

44 cm, Luas: 154 cm ²

2. 225

360

6 cm

Ringkasan Akhir

Dengan memahami konsep dasar, sifat-sifat, dan teknik penyelesaian yang tepat, siswa kelas 6 dapat menguasai soal cerita lingkaran. Pemahaman yang kuat tentang topik ini akan membekali mereka dengan keterampilan berpikir kritis dan pemecahan masalah yang berharga untuk kesuksesan mereka dalam matematika di masa depan.

Pertanyaan Umum yang Sering Muncul

Apa itu keliling lingkaran?

Keliling lingkaran adalah jarak di sekitar lingkaran.

Apa rumus keliling lingkaran?

K = πd atau K = 2πr

Apa itu luas lingkaran?

Luas lingkaran adalah daerah yang dibatasi oleh lingkaran.

Apa rumus luas lingkaran?

L = πr²