Lingkaran, salah satu bentuk geometri dasar, telah memikat pikiran para ahli matematika selama berabad-abad. Bentuk yang sederhana namun elegan ini memiliki sifat-sifat unik dan aplikasi yang luas, membuatnya menjadi topik yang penting dalam geometri.

Artikel ini akan memberikan gambaran menyeluruh tentang lingkaran, mulai dari definisi dan sifat-sifatnya hingga penerapannya dalam memecahkan masalah geometri dan dalam kehidupan sehari-hari. Dengan menjelajahi konsep inti dan mengasah keterampilan pemecahan masalah Anda melalui soal cerita, Anda akan memperoleh pemahaman yang lebih dalam tentang bentuk geometri yang menarik ini.

Konsep Lingkaran

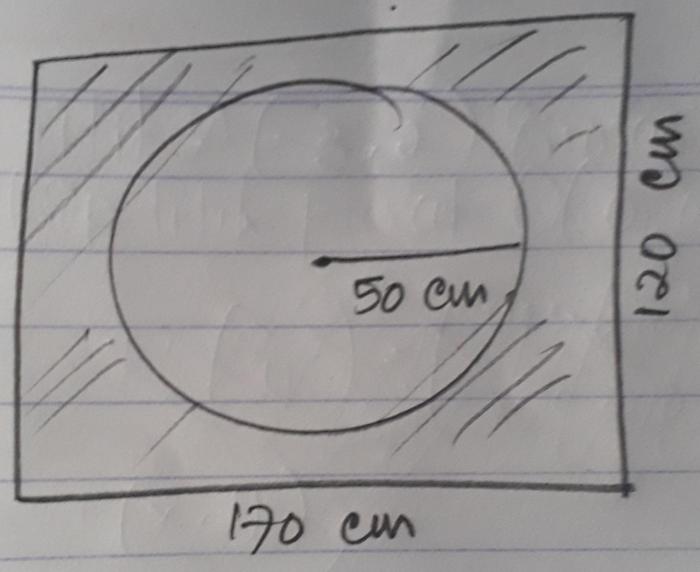
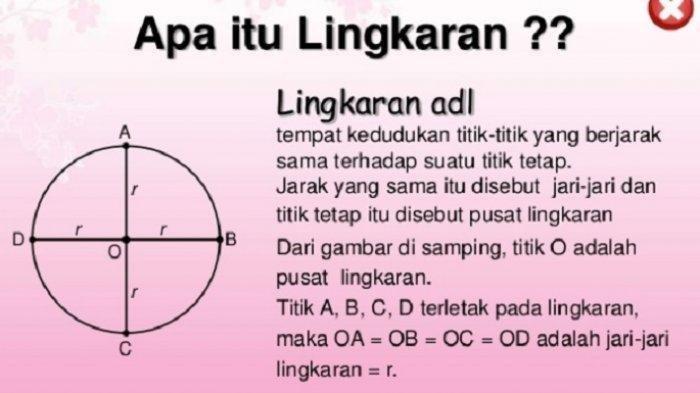
Lingkaran adalah kurva tertutup pada bidang yang mengelilingi titik tetap (disebut pusat) dan berjarak tetap dari titik tersebut (disebut jari-jari).

Rumus lingkaran:

Keliling = 2πr

Luas = πr ²

Sifat-sifat Lingkaran

• Semua titik pada lingkaran berjarak sama dari pusat.
• Garis yang menghubungkan dua titik pada lingkaran disebut tali busur.
• Diameter adalah tali busur yang melalui pusat lingkaran.
• Juring adalah daerah yang dibatasi oleh dua jari-jari dan sebuah busur.
• Tembereng adalah daerah yang dibatasi oleh dua jari-jari dan busur yang lebih kecil.

Penerapan Lingkaran dalam Kehidupan Sehari-hari

• Roda kendaraan
• Jam analog
• Cincin
• Lingkaran bola
• Orbit planet

Jenis-Jenis Lingkaran

Lingkaran adalah bentuk geometris yang dibatasi oleh satu titik pusat dan titik-titik lain yang berjarak sama dari titik pusat tersebut. Terdapat berbagai jenis lingkaran, masing-masing dengan karakteristik unik.

Lingkaran Biasa

Lingkaran biasa adalah lingkaran yang dibatasi oleh satu titik pusat dan satu jari-jari. Jari-jari adalah ruas garis yang menghubungkan titik pusat ke titik mana pun pada lingkaran.

Lingkaran Berpusat

Lingkaran berpusat adalah lingkaran yang dibatasi oleh dua titik pusat dan satu jari-jari. Jari-jari adalah ruas garis yang menghubungkan kedua titik pusat.

Lingkaran yang Dibatasi oleh Garis Singgung

Lingkaran yang dibatasi oleh garis singgung adalah lingkaran yang dibatasi oleh satu garis singgung dan satu titik pusat. Garis singgung adalah garis yang menyinggung lingkaran hanya pada satu titik.

Jenis Lingkaran	Sifat
Lingkaran Biasa	Dibatasi oleh satu titik pusat dan satu jari-jari
Lingkaran Berpusat	Dibatasi oleh dua titik pusat dan satu jari-jari
Lingkaran yang Dibatasi oleh Garis Singgung	Dibatasi oleh satu garis singgung dan satu titik pusat

Pengukuran Lingkaran

Lingkaran adalah bangun datar dua dimensi yang dibatasi oleh kurva tertutup yang disebut keliling. Pengukuran lingkaran melibatkan perhitungan keliling dan luasnya.

Keliling Lingkaran

• Rumus: K = 2πr
• Langkah-langkah:
1. Tentukan jari-jari lingkaran (r) dalam satuan yang sama (misalnya, cm, m).
2. Kalikan jari-jari dengan 2.
3. Kalikan hasil dengan π (3,14).

Luas Lingkaran

• Rumus: L = πr²
• Langkah-langkah:
1. Tentukan jari-jari lingkaran (r) dalam satuan yang sama (misalnya, cm, m).
2. Kuadratkan jari-jari (r x r).
3. Kalikan hasil dengan π (3,14).

Contoh Soal Cerita

Sebuah roda memiliki diameter 28 cm. Hitunglah keliling dan luas roda tersebut.

Solusi:

1. Keliling:
• Jari-jari = Diameter/2 = 28 cm/2 = 14 cm
• K = 2πr = 2 x 3,14 x 14 cm = 87,92 cm
2. Luas:
• r = 14 cm
• L = πr² = 3,14 x 14² cm² = 615,75 cm²

Relasi Lingkaran dengan Bangun Datar Lain

Lingkaran memiliki relasi khusus dengan bangun datar lainnya, seperti persegi, segitiga, dan trapesium. Relasi ini dapat digunakan untuk memecahkan masalah geometri.

Relasi dengan Persegi

• Lingkaran dapat dibatasi oleh persegi dengan cara yang disebut “lingkaran dalam”.
• Jari-jari lingkaran dalam sama dengan setengah diagonal persegi.
• Luas persegi sama dengan empat kali luas lingkaran dalam.

Relasi dengan Segitiga

• Lingkaran dapat dibatasi oleh segitiga sama sisi dengan cara yang disebut “lingkaran luar”.
• Jari-jari lingkaran luar sama dengan panjang sisi segitiga.
• Luas segitiga sama dengan setengah kali keliling segitiga dikalikan jari-jari lingkaran luar.

Relasi dengan Trapesium

Lingkaran dapat dibatasi oleh trapesium sama kaki dengan cara yang disebut “lingkaran tiga titik”.

• Lingkaran tiga titik bersinggungan dengan tiga titik pada trapesium

  dua titik pada sisi sejajar dan satu titik pada sisi yang tidak sejajar.

• Jari-jari lingkaran tiga titik sama dengan setengah tinggi trapesium.

Relasi ini dapat digunakan untuk memecahkan berbagai masalah geometri, seperti mencari luas atau keliling suatu bangun datar.

Aplikasi Lingkaran dalam Kehidupan Nyata

Lingkaran memiliki banyak aplikasi dalam berbagai bidang, dari teknik hingga seni. Bentuknya yang simetris dan dapat diprediksi menjadikannya alat yang serbaguna untuk memecahkan masalah dan menciptakan desain yang estetis.

Teknik

Dalam teknik, lingkaran digunakan untuk membuat struktur yang kuat dan efisien. Misalnya, roda, poros, dan bantalan semuanya mengandalkan bentuk lingkaran untuk berputar dengan lancar dan mendistribusikan beban secara merata.

Arsitektur

Di bidang arsitektur, lingkaran digunakan untuk menciptakan ruang yang harmonis dan estetis. Kubah, lengkungan, dan jendela bundar menambahkan sentuhan elegan dan mengundang pada bangunan. Lingkaran juga dapat digunakan untuk memaksimalkan ruang dan menciptakan efek optik yang menarik.

Seni

Dalam seni, lingkaran digunakan untuk menciptakan ilusi kedalaman, gerakan, dan harmoni. Pelukis dan pematung sering menggunakan lingkaran untuk menarik perhatian pemirsa dan menciptakan komposisi yang dinamis. Lingkaran juga merupakan motif yang umum dalam desain grafis dan logo, melambangkan kesatuan, kesempurnaan, dan tak terbatas.

Kesimpulan

Memahami soal cerita tentang lingkaran tidak hanya menguji kemampuan matematika Anda, tetapi juga melatih keterampilan berpikir kritis dan pemecahan masalah Anda. Dengan menguasai konsep-konsep yang mendasarinya dan menerapkannya secara efektif, Anda akan dilengkapi untuk menangani berbagai soal cerita tentang lingkaran dengan percaya diri.

Sudut Pertanyaan Umum (FAQ)

Apa itu soal cerita tentang lingkaran?

Soal cerita tentang lingkaran adalah soal matematika yang melibatkan penggunaan konsep lingkaran untuk memecahkan masalah yang disajikan dalam bentuk cerita.

Mengapa soal cerita tentang lingkaran penting?

Soal cerita tentang lingkaran penting karena membantu Anda memahami penerapan praktis konsep lingkaran dan mengembangkan keterampilan pemecahan masalah.

Apa saja jenis-jenis soal cerita tentang lingkaran?

Soal cerita tentang lingkaran dapat bervariasi, mulai dari menghitung keliling dan luas hingga memecahkan masalah yang melibatkan hubungan lingkaran dengan bangun datar lainnya.

Bagaimana cara memecahkan soal cerita tentang lingkaran?

Untuk memecahkan soal cerita tentang lingkaran, pertama-tama identifikasi informasi yang diberikan, gambar diagram untuk memvisualisasikan masalah, terapkan rumus yang sesuai, dan periksa kembali jawaban Anda.