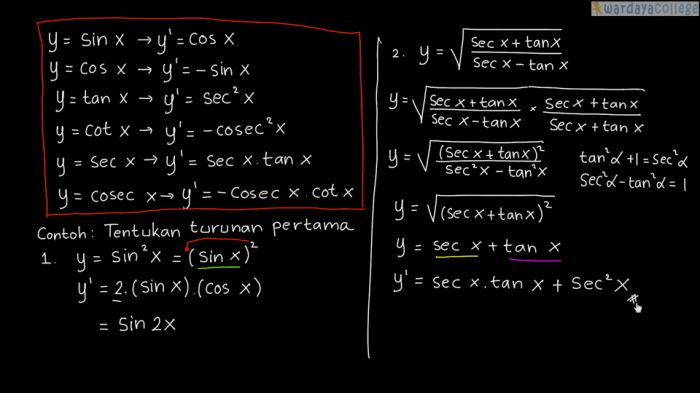Dalam dunia matematika, turunan fungsi trigonometri memegang peranan penting dalam memahami perilaku fungsi-fungsi ini. Turunan kedua, sebagai perpanjangan dari turunan pertama, memberikan wawasan lebih dalam tentang karakteristik dan aplikasi fungsi trigonometri.
Artikel ini akan mengupas secara komprehensif turunan kedua fungsi trigonometri, mencakup konsep dasarnya, rumus, tabel ringkasan, contoh soal, dan aplikasi praktisnya. Dengan pemahaman yang mendalam tentang topik ini, pembaca akan dilengkapi untuk menguasai aspek penting dari kalkulus trigonometri.
Turunan Pertama Fungsi Trigonometri

Dalam kalkulus, turunan suatu fungsi mengukur laju perubahan fungsi tersebut. Turunan fungsi trigonometri memainkan peran penting dalam berbagai aplikasi, seperti fisika, teknik, dan astronomi.
Turunan fungsi trigonometri dapat diperoleh dengan menggunakan aturan diferensiasi dasar. Aturan-aturan ini menyatakan bahwa turunan dari:
- sin(x) adalah cos(x)
- cos(x) adalah
-sin(x) - tan(x) adalah sec^2(x)
Turunan Kedua Fungsi Trigonometri
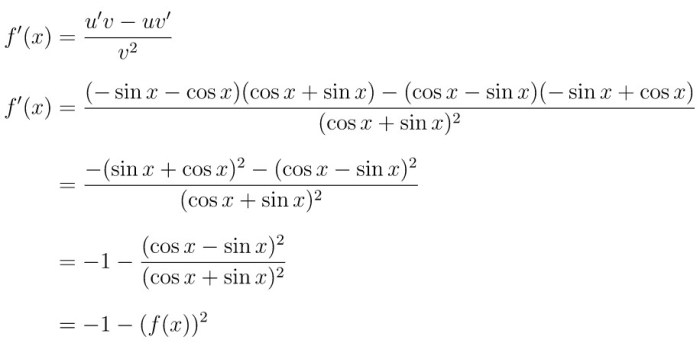
Turunan kedua fungsi trigonometri adalah turunan dari turunan pertama fungsi trigonometri. Turunan kedua ini memiliki peran penting dalam analisis fungsi trigonometri dan penerapannya dalam berbagai bidang.
Turunan Kedua Fungsi Trigonometri Umum
- sin(x):
-sin(x) - cos(x):
-cos(x) - tan(x): sec^2(x)
Aplikasi Turunan Kedua Fungsi Trigonometri
Turunan kedua fungsi trigonometri memiliki beberapa aplikasi penting, antara lain:
- Menentukan titik ekstrem (maksimum dan minimum) dari fungsi trigonometri.
- Mencari titik belok (infleksi) pada grafik fungsi trigonometri.
- Menyelidiki konveksitas dan konklafitas grafik fungsi trigonometri.
- Memecahkan masalah optimisasi yang melibatkan fungsi trigonometri.
Tabel Turunan Kedua Fungsi Trigonometri

Turunan kedua fungsi trigonometri memberikan informasi tentang laju perubahan turunan pertama. Tabel berikut merangkum turunan kedua dari fungsi trigonometri umum:
Fungsi Trigonometri Umum
- sin(x):
-sin(x) - cos(x):
-cos(x) - tan(x): sec2(x)
- cot(x):
-csc2(x) - sec(x): sec(x)tan(x)
- csc(x):
-csc(x)cot(x)
Hubungan dengan Turunan Pertama
Turunan kedua fungsi trigonometri terkait dengan turunan pertamanya melalui hubungan berikut:
- d2/dx2[sin(x)] =
-d/dx[sin(x)] - d2/dx2[cos(x)] =
-d/dx[cos(x)] - d2/dx2[tan(x)] = d/dx[sec2(x)]
- d2/dx2[cot(x)] =
-d/dx[csc2(x)] - d2/dx2[sec(x)] = sec(x)tan(x) + sec3(x)
- d2/dx2[csc(x)] =
-csc(x)cot(x)
– csc3(x)
Contoh Soal Turunan Kedua Fungsi Trigonometri

Untuk memahami konsep turunan kedua fungsi trigonometri, mari kita bahas contoh soal berikut:
Menghitung Turunan Kedua dari sin(x)
- Turunan pertama dari sin(x) adalah cos(x).
- Turunan kedua dari sin(x) adalah turunan dari cos(x), yang menghasilkan
sin(x).
Jadi, turunan kedua dari sin(x) adalah -sin(x) .
Aplikasi Turunan Kedua Fungsi Trigonometri
Turunan kedua fungsi trigonometri memiliki aplikasi yang luas dalam berbagai bidang, termasuk fisika, teknik, dan matematika. Turunan kedua ini memberikan informasi tentang kelengkungan grafik fungsi trigonometri, yang berguna untuk menganalisis osilasi, getaran, dan fenomena lainnya.
Aplikasi dalam Fisika
Dalam fisika, turunan kedua fungsi trigonometri digunakan untuk menganalisis gerak harmonik sederhana. Gerak harmonik sederhana adalah jenis gerak periodik yang terjadi ketika suatu benda mengalami gaya pemulih proporsional dengan perpindahannya dari titik kesetimbangan. Turunan kedua dari fungsi trigonometri yang menggambarkan gerak harmonik sederhana memberikan percepatan benda pada setiap titik waktu.
Aplikasi dalam Teknik
Dalam teknik, turunan kedua fungsi trigonometri digunakan untuk menganalisis getaran dan osilasi. Getaran adalah gerakan bolak-balik suatu benda di sekitar titik kesetimbangannya, sedangkan osilasi adalah perubahan periodik suatu besaran fisika. Turunan kedua dari fungsi trigonometri yang menggambarkan getaran atau osilasi memberikan frekuensi dan amplitudo gerakan.
Aplikasi dalam Matematika
Dalam matematika, turunan kedua fungsi trigonometri digunakan untuk menentukan titik balik dan titik belok pada grafik fungsi. Titik balik adalah titik di mana fungsi berubah dari meningkat ke menurun atau sebaliknya, sedangkan titik belok adalah titik di mana fungsi berubah dari cekung ke cembung atau sebaliknya.
Turunan kedua dari fungsi trigonometri memberikan informasi tentang sifat titik-titik ini.
Simpulan Akhir
Dengan mengeksplorasi turunan kedua fungsi trigonometri, kita memperoleh pemahaman yang lebih komprehensif tentang perilaku fungsi-fungsi ini. Pengetahuan ini sangat penting dalam berbagai bidang, mulai dari fisika dan teknik hingga matematika murni. Melalui aplikasi praktis dan contoh nyata, kita dapat menghargai kekuatan turunan kedua dalam menyelesaikan masalah dan memodelkan fenomena dunia nyata.
Pertanyaan Umum (FAQ)
Apa perbedaan antara turunan pertama dan kedua?
Turunan pertama mengukur laju perubahan suatu fungsi, sedangkan turunan kedua mengukur laju perubahan dari laju perubahan tersebut.
Apakah ada hubungan antara turunan pertama dan kedua?
Ya, turunan kedua adalah turunan dari turunan pertama.
Di mana turunan kedua fungsi trigonometri digunakan?
Turunan kedua digunakan dalam berbagai aplikasi, seperti menentukan titik ekstrem, menganalisis grafik fungsi, dan menyelesaikan persamaan diferensial.