Fungsi eksponensial merupakan konsep fundamental dalam matematika yang memodelkan pertumbuhan atau peluruhan eksponensial. Grafik fungsi ini memiliki karakteristik unik yang membedakannya dari jenis fungsi lainnya, menjadikannya alat yang ampuh untuk berbagai aplikasi di berbagai bidang.
Dalam artikel ini, kita akan membahas dasar-dasar grafik fungsi eksponensial, langkah-langkah menggambarnya, contoh soal dan pembahasan, serta aplikasinya. Selain itu, kita juga akan mengeksplorasi sifat-sifat grafik fungsi eksponensial yang mempengaruhi bentuk dan interpretasinya.
Konsep Dasar Grafik Fungsi Eksponensial
Fungsi eksponensial adalah fungsi matematika yang menyatakan hubungan antara variabel independen dan dependen di mana variabel dependen (y) meningkat atau menurun secara eksponensial seiring perubahan variabel independen (x).
Contoh fungsi eksponensial:
- y = 2x
- y = ex
- y = 10x
Ciri-ciri grafik fungsi eksponensial:
- Bentuk melengkung ke atas (fungsi eksponensial positif) atau ke bawah (fungsi eksponensial negatif)
- Memotong sumbu y pada titik (0, 1)
- Tidak memiliki titik maksimum atau minimum
- Memiliki asimtot horizontal pada sumbu x (y = 0)
Cara Menggambar Grafik Fungsi Eksponensial
Fungsi eksponensial adalah fungsi yang bentuk umumnya adalah y = a x , di mana a adalah basis positif dan x adalah eksponen. Grafik fungsi eksponensial memiliki bentuk karakteristik yang berbeda, tergantung pada nilai a .
Langkah-Langkah Menggambar Grafik Fungsi Eksponensial
- Susun tabel nilai. Pilih beberapa nilai x dan hitung nilai y yang sesuai menggunakan persamaan fungsi yang diberikan.
- Plot titik-titik. Pada bidang koordinat, plot titik-titik (x, y) yang telah dihitung.
- Gambar grafik. Hubungkan titik-titik yang telah diplot dengan kurva halus. Bentuk kurva akan tergantung pada nilai a. Untuk a > 1, grafik akan meningkat dengan cepat. Untuk 0 < a < 1, grafik akan menurun dengan cepat.
Contoh Soal dan Pembahasan

Berikut ini adalah contoh soal grafik fungsi eksponensial beserta pembahasannya:
Soal
Tentukan grafik fungsi eksponensial dari persamaan berikut:
$$y = 2^x$$
Pembahasan
Untuk menentukan grafik fungsi eksponensial, kita dapat membuat tabel nilai terlebih dahulu:
| x | y ||—|—||
2 | 0,25 |
|
1 | 0,5 |
| 0 | 1 || 1 | 2 || 2 | 4 |
Dengan menggunakan tabel nilai tersebut, kita dapat memplot grafik fungsi eksponensial sebagai berikut:
[Gambar grafik fungsi eksponensial y = 2^x]
Dari grafik tersebut, kita dapat melihat bahwa fungsi eksponensial y = 2^x memiliki bentuk kurva yang naik secara eksponensial. Fungsi ini memiliki titik potong sumbu y di titik (0, 1) dan tidak memiliki titik potong sumbu x.
Aplikasi Grafik Fungsi Eksponensial
Grafik fungsi eksponensial banyak digunakan dalam berbagai bidang untuk memodelkan berbagai fenomena dan membuat prediksi. Grafik ini sangat berguna untuk merepresentasikan perubahan yang terjadi secara eksponensial, yaitu perubahan yang semakin cepat atau lambat secara proporsional.
Bidang Sains
Dalam sains, grafik fungsi eksponensial digunakan untuk:
- Memperkirakan pertumbuhan populasi bakteri atau virus
- Memodelkan peluruhan radioaktif
- Menghitung waktu paruh suatu zat
Bidang Ekonomi
Dalam ekonomi, grafik fungsi eksponensial digunakan untuk:
- Memprediksi pertumbuhan ekonomi
- Memodelkan nilai investasi
- Menghitung bunga majemuk
Bidang Teknik
Dalam teknik, grafik fungsi eksponensial digunakan untuk:
- Memodelkan pertumbuhan jaringan komputer
- Menganalisis kerusakan material
- Merancang sistem kontrol
Sifat-Sifat Grafik Fungsi Eksponensial

Grafik fungsi eksponensial memiliki sifat-sifat unik yang membedakannya dari jenis grafik lainnya. Sifat-sifat ini mencakup asimtot, titik potong sumbu, dan interval naik/turun.
Asimtot
Grafik fungsi eksponensial memiliki dua asimtot, yaitu asimtot horizontal dan asimtot vertikal.
- Asimtot Horizontal: Garis horizontal yang didekati grafik saat x mendekati tak hingga positif atau negatif. Asimtot horizontal diberikan oleh persamaan y = 0.
- Asimtot Vertikal: Garis vertikal yang didekati grafik saat x mendekati suatu nilai tertentu. Asimtot vertikal diberikan oleh persamaan x = a, di mana a adalah nilai yang tidak termasuk dalam domain fungsi.
Titik Potong Sumbu
Grafik fungsi eksponensial memotong sumbu y pada titik (0, 1) dan tidak memotong sumbu x .
Interval Naik/Turun
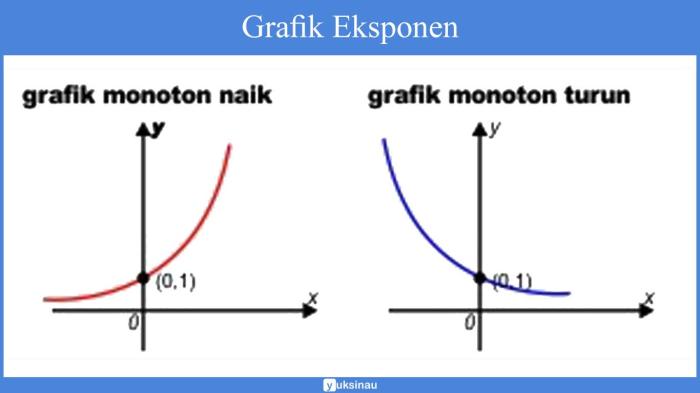
Grafik fungsi eksponensial selalu naik atau selalu turun tergantung pada nilai basisnya:
- Basis > 1: Grafik naik untuk semua nilai x.
- Basis < 1: Grafik turun untuk semua nilai x.
Ringkasan Terakhir

Memahami grafik fungsi eksponensial sangat penting untuk berbagai disiplin ilmu, termasuk matematika, sains, dan ekonomi. Dengan memahami konsep dan sifat-sifatnya, kita dapat memperoleh wawasan yang berharga tentang fenomena dunia nyata yang menunjukkan pertumbuhan atau peluruhan eksponensial. Selain itu, kemampuan untuk menggambar dan menganalisis grafik fungsi eksponensial sangat penting untuk menyelesaikan masalah dan membuat prediksi yang akurat.
Tanya Jawab (Q&A)
Apa saja sifat-sifat umum grafik fungsi eksponensial?
Grafik fungsi eksponensial memiliki beberapa sifat umum, seperti asimtot horizontal, titik potong sumbu y, dan interval naik/turun yang ditentukan oleh pangkat eksponen.
Bagaimana cara menentukan asimtot horizontal grafik fungsi eksponensial?
Asimtot horizontal dari grafik fungsi eksponensial adalah garis y = 0, yang menunjukkan bahwa grafik tersebut mendekati garis ini saat x mendekati tak terhingga positif atau negatif.
Bagaimana cara mengidentifikasi titik potong sumbu y grafik fungsi eksponensial?
Titik potong sumbu y dari grafik fungsi eksponensial adalah titik (0, 1), yang merupakan titik di mana grafik memotong sumbu y.
Apa perbedaan antara fungsi eksponensial dan fungsi polinomial?
Fungsi eksponensial memiliki pangkat eksponen yang bervariasi dengan x, sedangkan fungsi polinomial memiliki pangkat eksponen yang tetap.
