Dalam dunia transformasi geometri, dilatasi memegang peranan penting. Dilatasi adalah perubahan ukuran dan bentuk suatu bangun datar atau bangun ruang tanpa mengubah bentuk aslinya. Memahami dilatasi sangat krusial dalam berbagai bidang, mulai dari teknik hingga desain.
Artikel ini akan menyajikan pemahaman komprehensif tentang dilatasi, jenis-jenisnya, cara melakukannya, contoh soal, dan aplikasinya dalam kehidupan nyata. Dengan panduan ini, Anda akan menguasai konsep dilatasi dan menerapkannya secara efektif.
Pengertian Dilatasi
Dalam transformasi geometri, dilatasi adalah transformasi yang mengubah ukuran suatu bangun geometri tanpa mengubah bentuknya. Bangun geometri yang mengalami dilatasi disebut bangun asli, sedangkan bangun geometri hasil dilatasi disebut bangun bayangan.
Dilatasi dilakukan dengan cara memperbesar atau memperkecil bangun asli dengan faktor skala tertentu. Faktor skala adalah bilangan positif yang menentukan perbandingan ukuran bangun bayangan terhadap bangun asli.
Ilustrasi Visual
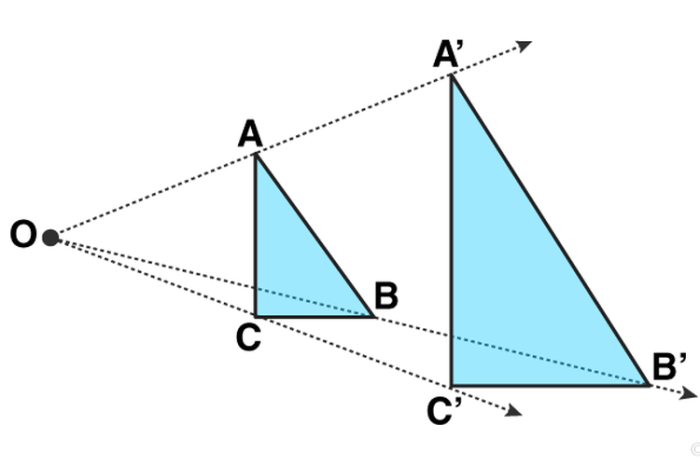
Berikut adalah ilustrasi visual yang menggambarkan dilatasi:
- Bangun asli (segitiga biru)
- Faktor skala = 2
- Bangun bayangan (segitiga merah)
Pada ilustrasi tersebut, segitiga biru merupakan bangun asli dan segitiga merah merupakan bangun bayangan. Faktor skala yang digunakan adalah 2, yang berarti bahwa segitiga merah memiliki ukuran dua kali lebih besar dari segitiga biru.
Jenis-Jenis Dilatasi
Dilatasi adalah transformasi geometri yang mengubah ukuran dan bentuk suatu objek tanpa mengubah posisinya. Dilatasi dapat diklasifikasikan menjadi dua jenis utama:
Dilatasi Isotropik
Dalam dilatasi isotropik, semua arah objek diperbesar atau diperkecil dengan faktor yang sama. Dengan kata lain, objek mempertahankan bentuknya tetapi berubah ukurannya. Contoh dilatasi isotropik adalah ketika kita memperbesar atau memperkecil foto.
Dilatasi Anisotropik
Dalam dilatasi anisotropik, objek diperbesar atau diperkecil dengan faktor yang berbeda dalam arah yang berbeda. Hal ini dapat menyebabkan perubahan bentuk objek. Contoh dilatasi anisotropik adalah ketika kita meregangkan atau mengompres suatu benda.
Cara Melakukan Dilatasi
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun datar atau garis dengan faktor skala tertentu. Berikut langkah-langkah melakukan dilatasi:
Dilatasi Titik
- Tentukan titik pusat dilatasi.
- Tentukan faktor skala.
- Gambar vektor dari titik pusat ke titik yang akan didilatasi.
- Kalikan panjang vektor dengan faktor skala.
- Gambar vektor baru dengan panjang yang sama dengan hasil perkalian dan arah yang sama dengan vektor asli.
- Titik akhir vektor baru adalah titik yang didilatasikan.
Dilatasi Garis
- Tentukan garis yang akan didilatasikan.
- Tentukan titik pusat dilatasi.
- Tentukan faktor skala.
- Dilatasi setiap titik pada garis dengan menggunakan langkah-langkah dilatasi titik.
- Hubungkan titik-titik yang telah didilatasikan untuk membentuk garis baru.
Dilatasi Bangun Datar
- Tentukan bangun datar yang akan didilatasikan.
- Tentukan titik pusat dilatasi.
- Tentukan faktor skala.
- Dilatasi setiap titik pada bangun datar dengan menggunakan langkah-langkah dilatasi titik.
- Hubungkan titik-titik yang telah didilatasikan untuk membentuk bangun datar baru.
Prinsip-Prinsip Dilatasi
- Titik pusat dilatasi tetap tidak berubah.
- Faktor skala harus bernilai positif.
- Bangun datar yang didilatasikan memiliki bentuk yang sama dengan bangun datar asli.
- Panjang sisi bangun datar yang didilatasikan akan berubah dengan faktor skala.
- Luas bangun datar yang didilatasikan akan berubah dengan faktor skala kuadrat.
- Volume bangun ruang yang didilatasikan akan berubah dengan faktor skala kubik.
Contoh Soal Dilatasi
Dilatasi adalah transformasi geometri yang memperbesar atau memperkecil suatu bangun geometri dengan faktor tertentu. Berikut beberapa contoh soal dilatasi:
Dilatasi Isotropik
Dilatasi isotropik memperbesar atau memperkecil suatu bangun geometri dengan faktor yang sama pada semua arah.
Soal:
Segitiga ABC memiliki panjang sisi AB = 5 cm, BC = 6 cm, dan CA = 7 cm. Dilatasi segitiga ABC dengan faktor skala 2 menghasilkan segitiga A’B’C’. Tentukan panjang sisi A’B’, B’C’, dan C’A’ pada segitiga A’B’C’.
Dilatasi Anisotropik
Dilatasi anisotropik memperbesar atau memperkecil suatu bangun geometri dengan faktor yang berbeda pada arah yang berbeda.
Soal:
Sebuah persegi panjang ABCD memiliki panjang 8 cm dan lebar 5 cm. Dilatasi persegi panjang ABCD dengan faktor skala 2 pada arah horizontal dan 3 pada arah vertikal menghasilkan persegi panjang A’B’C’D’. Tentukan panjang dan lebar persegi panjang A’B’C’D’.
Dilatasi Terhadap Garis
Dilatasi terhadap garis memperbesar atau memperkecil suatu bangun geometri dengan faktor tertentu terhadap garis tertentu.
Soal:
Sebuah segitiga PQR memiliki panjang sisi PQ = 10 cm, QR = 12 cm, dan RP = 8 cm. Dilatasi segitiga PQR terhadap garis QR dengan faktor skala 1,5 menghasilkan segitiga P’Q’R’. Tentukan panjang sisi P’Q’, Q’R’, dan R’P’ pada segitiga P’Q’R’.
Jawaban Soal Dilatasi

Soal dilatasi yang diberikan adalah sebagai berikut:
Dilatasikan segitiga ABC dengan pusat O dan faktor skala 2. Jika koordinat titik A(-2, 3), B(1,
1), dan C(4, 2), tentukan koordinat titik A’, B’, dan C’ setelah dilatasi.
Untuk menjawab soal ini, kita gunakan rumus dilatasi titik (x, y) dengan pusat (a, b) dan faktor skala k sebagai berikut:
x’ = k(x
a) + a
y’ = k(y
b) + b
Koordinat Titik A’
- x’ = 2((-2)
– 0) + 0 =
-4 - y’ = 2(3
– 0) + 0 = 6
Jadi, koordinat titik A’ adalah (-4, 6).
Koordinat Titik B’
- x’ = 2((1)
– 0) + 0 = 2 - y’ = 2((-1)
– 0) + 0 =
-2
Jadi, koordinat titik B’ adalah (2,
2).
Koordinat Titik C’
- x’ = 2((4)
– 0) + 0 = 8 - y’ = 2((2)
– 0) + 0 = 4
Jadi, koordinat titik C’ adalah (8, 4).
Berikut adalah diagram yang menunjukkan segitiga ABC dan segitiga A’B’C’ setelah dilatasi:

Aplikasi Dilatasi dalam Kehidupan Nyata

Dilatasi memiliki berbagai aplikasi praktis di berbagai bidang, termasuk teknik, desain, dan lainnya. Aplikasi ini memanfaatkan sifat dilatasi yang mengubah ukuran dan bentuk suatu objek tanpa mengubah proporsinya.
Salah satu aplikasi penting dilatasi adalah dalam pembuatan jembatan. Insinyur menggunakan prinsip dilatasi untuk memperhitungkan perubahan suhu yang dapat menyebabkan jembatan memuai atau menyusut. Dengan mengompensasi perubahan ini, mereka dapat memastikan bahwa jembatan tetap aman dan dapat diandalkan.
Aplikasi dalam Desain
Dalam desain, dilatasi digunakan untuk membuat objek yang skalanya berbeda-beda. Misalnya, arsitek dapat menggunakan dilatasi untuk membuat denah lantai bangunan yang skalanya lebih kecil atau lebih besar. Ini memudahkan mereka untuk memvisualisasikan dan merencanakan tata letak bangunan.
Aplikasi dalam Industri
Dalam industri, dilatasi digunakan untuk memproduksi berbagai komponen dengan ukuran dan bentuk yang tepat. Misalnya, dalam pembuatan mobil, dilatasi digunakan untuk membentuk logam menjadi bagian bodi mobil. Ini memastikan bahwa bagian-bagian tersebut pas satu sama lain dan berfungsi dengan benar.
Ringkasan Penutup

Dilatasi adalah konsep transformasi geometri yang sangat penting dengan aplikasi luas dalam berbagai bidang. Dengan memahami konsep, jenis, dan cara melakukan dilatasi, kita dapat menyelesaikan masalah geometri kompleks dan membuat desain yang optimal. Contoh soal dan jawaban yang disediakan dalam artikel ini berfungsi sebagai referensi praktis untuk mengasah keterampilan dilatasi Anda.
Pertanyaan Umum yang Sering Muncul
Apa saja jenis-jenis dilatasi?
Dilatasi dapat dibedakan menjadi dua jenis: dilatasi isotropik (seragam) dan dilatasi anisotropik (tidak seragam).
Bagaimana cara melakukan dilatasi titik?
Untuk mendilatasikan titik, kalikan koordinat titik dengan faktor skala yang sama.
Apa saja aplikasi dilatasi dalam kehidupan nyata?
Dilatasi digunakan dalam arsitektur, desain industri, dan pembuatan peta untuk mengubah ukuran dan skala objek secara akurat.