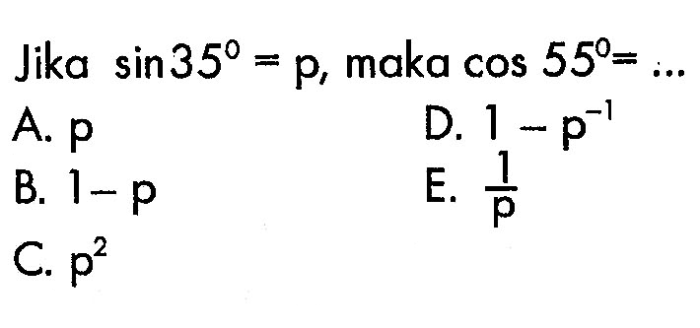Dalam trigonometri, sinus dan kosinus merupakan fungsi yang mendefinisikan hubungan antara sisi segitiga siku-siku dan sudutnya. Identitas trigonometri yang menarik menghubungkan nilai sinus dan kosinus untuk sudut komplementer, di mana sin(90° – θ) = cos(θ).
Salah satu identitas penting adalah sin 35° = cos 55°. Identitas ini memiliki banyak aplikasi praktis, seperti dalam navigasi dan teknik. Artikel ini akan membahas bukti aljabar, penerapan, dan contoh identitas ini.
Definisi Sinus dan Kosinus
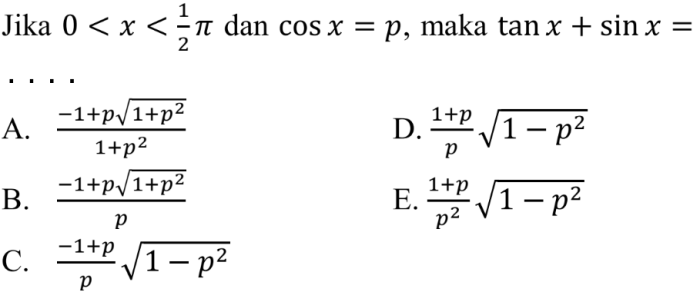
Dalam trigonometri, sinus dan kosinus adalah fungsi trigonometri yang digunakan untuk menentukan hubungan antara sudut dan panjang sisi dalam segitiga siku-siku.
Rumus untuk menghitung sinus dan kosinus dari sudut θ adalah:
- sin θ = sisi depan / sisi miring
- cos θ = sisi samping / sisi miring
Hubungan antara Sinus dan Kosinus
Sinus dan kosinus adalah dua fungsi trigonometri yang saling terkait. Identitas trigonometri menghubungkan nilai-nilai sinus dan kosinus dari sudut yang sama. Salah satu identitas penting adalah cos(90° – θ) = sin(θ).
Identitas cos(90°
θ) = sin(θ)
θ) = sin(θ)
Identitas cos(90° – θ) = sin(θ) menyatakan bahwa kosinus dari sudut komplementer (yaitu, sudut yang jumlahnya 90°) sama dengan sinus dari sudut asli. Ini dapat dibuktikan menggunakan definisi sinus dan kosinus dalam lingkaran satuan.
Bukti Identitas sin(35°) = cos(55°)
Dalam trigonometri, identitas sin(35°) = cos(55°) adalah hubungan penting yang dapat dibuktikan secara aljabar menggunakan identitas trigonometri yang relevan.
Langkah-langkah Bukti
- Mulai dengan identitas trigonometri dasar: sin(90°
θ) = cos(θ).
- Substitusi θ = 35° ke dalam identitas, sehingga diperoleh sin(90°
35°) = cos(35°).
- Sederhanakan 90°
35° = 55°, sehingga sin(55°) = cos(35°).
- Oleh karena itu, terbukti bahwa sin(35°) = cos(55°).
Penerapan Praktis
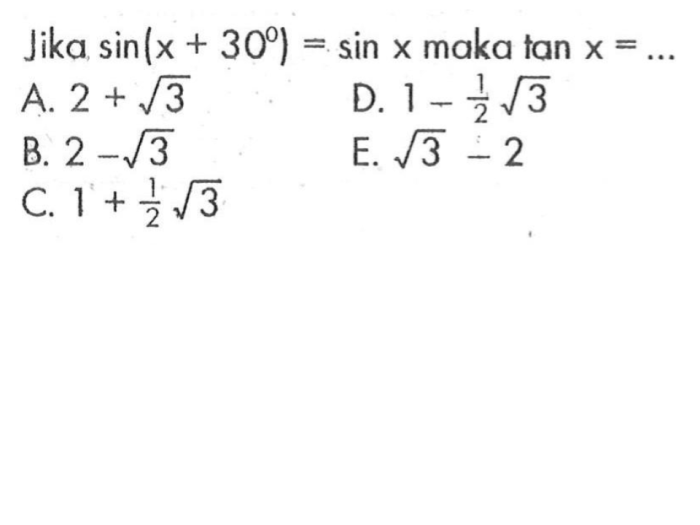
Identitas sin(35°) = cos(55°) memiliki aplikasi praktis yang signifikan dalam berbagai bidang, termasuk navigasi dan teknik.
Dalam navigasi, identitas ini digunakan untuk menghitung sudut antara dua titik di permukaan bumi. Dalam teknik, identitas ini digunakan untuk merancang dan menganalisis struktur yang mengalami gaya sudut, seperti jembatan dan gedung.
Navigasi
Dalam navigasi, identitas sin(35°) = cos(55°) digunakan untuk menentukan sudut antara dua titik di permukaan bumi. Sudut ini dikenal sebagai “bearing,” dan merupakan informasi penting untuk menentukan arah perjalanan.
Untuk menghitung bearing, navigator menggunakan rumus berikut:
bearing = tan -1 ((cos(latitude1)
- sin(latitude2)
- sin(latitude1)
- cos(latitude2)
- cos(longitude2
- longitude1)) / (sin(latitude1)
- sin(latitude2) + cos(latitude1)
- cos(latitude2)
- cos(longitude2
- longitude1)))
Dalam rumus ini, latitude1 dan longitude1 adalah koordinat titik awal, dan latitude2 dan longitude2 adalah koordinat titik akhir.
Teknik
Dalam teknik, identitas sin(35°) = cos(55°) digunakan untuk merancang dan menganalisis struktur yang mengalami gaya sudut. Struktur ini meliputi jembatan, gedung, dan tiang listrik.
Gaya sudut dapat menyebabkan struktur mengalami defleksi atau lentur. Untuk mencegah kegagalan struktural, insinyur harus merancang struktur yang dapat menahan gaya-gaya ini.
Identitas sin(35°) = cos(55°) digunakan untuk menghitung besarnya gaya sudut yang bekerja pada suatu struktur. Gaya ini kemudian digunakan untuk menghitung defleksi atau lentur struktur.
Contoh dan Prosedur
Identitas trigonometri sin(θ) = cos(90° – θ) dapat dibuktikan menggunakan tabel nilai trigonometri atau dengan menerapkan langkah-langkah aljabar.
Berikut ini adalah beberapa contoh dan prosedur yang dapat digunakan untuk membuktikan identitas ini:
Membuat Tabel Nilai Trigonometri
Buat tabel yang menunjukkan nilai sin(θ) dan cos(90° – θ) untuk sudut yang berbeda. Misalnya:
| θ | sin(θ) | cos(90°
|
|---|---|---|
| 0° | 0 | 1 |
| 30° | 1/2 | √3/2 |
| 45° | √2/2 | √2/2 |
| 60° | √3/2 | 1/2 |
| 90° | 1 | 0 |
Dari tabel tersebut, dapat dilihat bahwa untuk setiap sudut θ, nilai sin(θ) sama dengan nilai cos(90° – θ).
Membuktikan Secara Aljabar
Identitas sin(θ) = cos(90° – θ) juga dapat dibuktikan secara aljabar dengan menggunakan rumus-rumus trigonometri:
- sin(θ) = cos(90°
– θ) - cos(θ) = sin(90°
– θ)
Misalnya, untuk membuktikan sin(35°) = cos(55°), dapat digunakan langkah-langkah berikut:
- Tuliskan persamaan sin(35°) = cos(90°
35°).
- Gunakan rumus cos(θ) = sin(90°
- θ) untuk menggantikan cos(90°
- 35°) dengan sin(35°).
- Sederhanakan persamaan menjadi sin(35°) = sin(35°).
- Karena kedua sisi persamaan sama, maka identitas sin(35°) = cos(55°) terbukti.
Ilustrasi Grafis
Hubungan antara sinus dan kosinus pada lingkaran satuan dapat diilustrasikan dengan segitiga siku-siku yang sisi miringnya memiliki panjang 1. Sudut yang dibentuk oleh sisi yang berlawanan dengan sudut 35° adalah sudut 55°.
Dalam segitiga ini, sinus 35° didefinisikan sebagai rasio sisi yang berlawanan (panjangnya y) dengan sisi miring (panjangnya 1). Kosinus 55° didefinisikan sebagai rasio sisi yang berdekatan (panjangnya x) dengan sisi miring.
Diagram Bukti Aljabar
Identitas sin(35°) = cos(55°) dapat dibuktikan secara aljabar menggunakan rumus setengah sudut:
sin(35°) = √((1
cos(70°)) / 2)
cos(55°) = √((1 + cos(70°)) / 2)
Dengan mensubstitusi cos(70°) = -cos(10°), kita mendapatkan:
sin(35°) = √((1
(-cos(10°))) / 2) = √((1 + cos(10°)) / 2)
= cos(55°)
Ringkasan Akhir

Identitas sin 35° = cos 55° memberikan wawasan berharga tentang hubungan antara sinus dan kosinus. Identitas ini memiliki aplikasi yang luas dalam bidang seperti navigasi dan teknik. Bukti aljabar yang jelas dan contoh praktis yang diberikan dalam artikel ini semakin memperkuat pemahaman tentang identitas penting ini.
Tanya Jawab (Q&A)
Mengapa identitas sin 35° = cos 55° penting?
Identitas ini penting karena menyederhanakan perhitungan trigonometri dan memiliki aplikasi praktis dalam bidang seperti navigasi dan teknik.
Bagaimana cara membuktikan identitas sin 35° = cos 55°?
Bukti aljabar melibatkan penggunaan identitas trigonometri seperti cos(90° – θ) = sin(θ) dan sin(θ + 90°) = cos(θ).
Di mana identitas sin 35° = cos 55° digunakan?
Identitas ini digunakan dalam navigasi untuk menghitung jarak dan arah, serta dalam teknik untuk merancang struktur dan mesin.