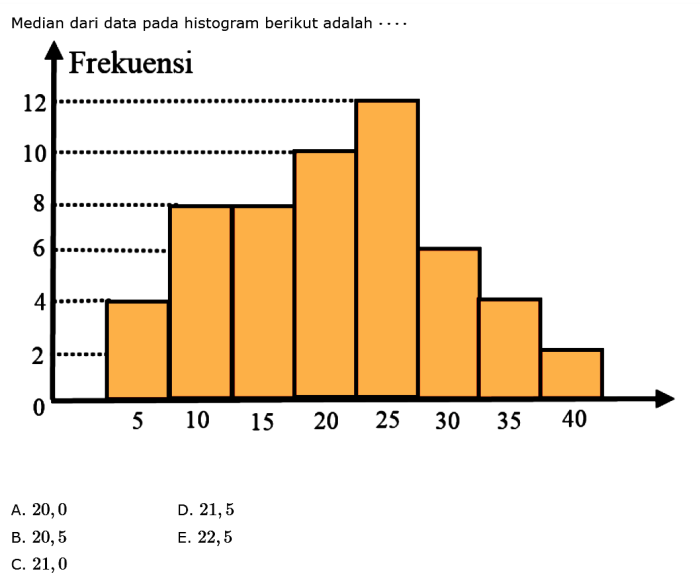
Median dari data pada tabel berikut adalah – Median, ukuran pemusatan data yang penting, memberikan wawasan tentang nilai tengah dalam sekumpulan data. Berbeda dengan rata-rata, median tidak terpengaruh oleh nilai ekstrem dan memberikan representasi yang lebih akurat dari data yang miring.
Artikel ini memberikan panduan komprehensif tentang median, mencakup pengertian, metode perhitungan, aplikasi, dan keterbatasannya. Melalui contoh dan penjelasan langkah demi langkah, kita akan mengeksplorasi peran penting median dalam statistik dan analisis data.
Pengertian Median
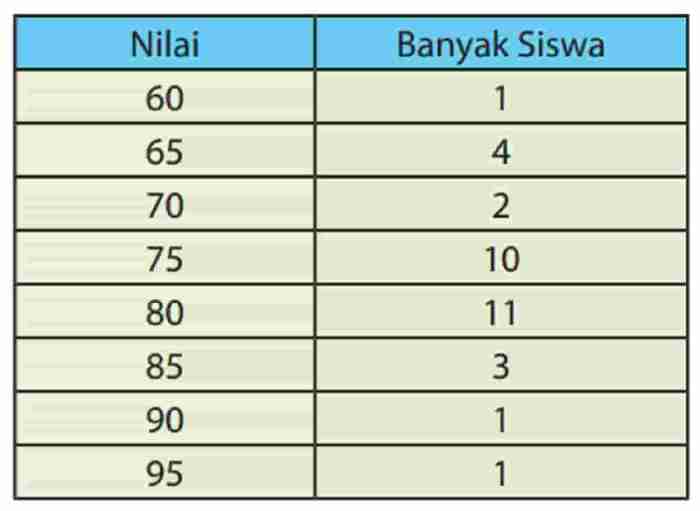
Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan dari nilai terkecil ke nilai terbesar. Median membagi kumpulan data menjadi dua bagian yang sama besar, di mana setengah data berada di bawah median dan setengah lainnya berada di atas median.
Median dari data pada tabel berikut adalah nilai tengah yang memisahkan setengah dari data di atasnya dan setengah di bawahnya. Dalam ilmu ekonomi, konsep opportunity cost juga mengacu pada nilai yang dikorbankan ketika memilih satu pilihan dibandingkan yang lain. Dengan demikian, median dapat membantu dalam memahami trade-off yang terkait dengan pengambilan keputusan, dengan mempertimbangkan biaya peluang yang menyertainya.
Menghitung Median, Median dari data pada tabel berikut adalah
Untuk menghitung median, data harus diurutkan terlebih dahulu. Jika jumlah data ganjil, median adalah nilai tengah dari data yang telah diurutkan. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Contoh
Misalkan kita memiliki kumpulan data berikut: 2, 4, 5, 7, 9. Setelah diurutkan, menjadi: 2, 4, 5, 7, 9. Karena jumlah data ganjil, median adalah nilai tengah, yaitu 5.
Sifat-Sifat Median
- Median tidak terpengaruh oleh nilai ekstrem (outlier).
- Median lebih stabil dibandingkan rata-rata (mean) terhadap perubahan data.
- Median dapat digunakan untuk data yang tidak berdistribusi normal.
Cara Menghitung Median

Median adalah nilai tengah dari sekumpulan data yang telah diurutkan. Untuk menghitung median, ikuti langkah-langkah berikut:
Urutkan Data
Susun data dalam urutan menaik atau menurun.
Median dari data pada tabel berikut adalah nilai yang membagi data menjadi dua bagian yang sama. Hal ini menunjukkan kecenderungan tengah dari data. Dalam konteks materi tanah dan keberlangsungan kehidupan , median dapat digunakan untuk membandingkan sifat fisik dan kimia tanah yang berbeda dan menentukan kesesuaiannya untuk mendukung kehidupan tanaman.
Dengan memahami median, kita dapat mengidentifikasi tanah yang optimal untuk pertanian, konservasi, dan tujuan lingkungan lainnya.
Tentukan Titik Tengah
Tentukan titik tengah data. Jika jumlah data ganjil, median adalah nilai titik tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Contoh
Misalkan kita memiliki kumpulan data berikut: 2, 4, 6, 8, 10.
- Urutkan data: 2, 4, 6, 8, 10
- Jumlah data ganjil, jadi median adalah nilai titik tengah: 6
Median Data Berkelompok
Jika data disajikan dalam bentuk data berkelompok, maka rumus berikut dapat digunakan untuk menghitung median:
Median = L + (n/2
- F)
- i / f
- L = Batas bawah kelas median
- n = Jumlah total data
- F = Frekuensi kumulatif kelas sebelum kelas median
- i = Lebar kelas
- f = Frekuensi kelas median
Contoh Perhitungan Median: Median Dari Data Pada Tabel Berikut Adalah

Median adalah nilai tengah dalam suatu kumpulan data yang telah diurutkan. Untuk menghitung median, data harus diurutkan dari yang terkecil hingga terbesar.
Menghitung Median Data Ganjil
Jika jumlah data ganjil, median adalah nilai tengah. Misalnya, jika kita memiliki data 5, 7, 9, 11, 13, maka mediannya adalah 9, yang merupakan nilai tengah.
Menghitung Median Data Genap
Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah. Misalnya, jika kita memiliki data 5, 7, 9, 11, mediannya adalah (9 + 11) / 2 = 10.
Langkah-langkah Menghitung Median
- Urutkan data dari yang terkecil hingga terbesar.
- Jika jumlah data ganjil, median adalah nilai tengah.
- Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Contoh Perhitungan
Misalkan kita memiliki data: 10, 12, 15, 18, 20. Untuk menghitung median:
- Urutkan data: 10, 12, 15, 18, 20.
- Karena jumlah data ganjil, median adalah nilai tengah, yaitu 15.
Aplikasi Median

Median adalah ukuran tendensi sentral yang banyak digunakan dalam statistik. Ini memberikan nilai tengah dari suatu kumpulan data ketika diurutkan dari terkecil ke terbesar.
Median memiliki beberapa kegunaan penting:
Penerapan Median dalam Kehidupan Nyata
- Mengidentifikasi nilai tengah dari suatu distribusi data, seperti pendapatan rumah tangga atau nilai ujian.
- Membandingkan dua atau lebih kelompok data, seperti kinerja dua tim olahraga atau hasil penjualan dua produk yang berbeda.
- Mendeteksi pencilan atau nilai ekstrem dalam suatu kumpulan data, yang dapat mempengaruhi nilai rata-rata.
Perbedaan antara Median, Mean, dan Modus
Median berbeda dari dua ukuran tendensi sentral lainnya, yaitu mean (rata-rata) dan modus:
- Meanadalah jumlah semua nilai data dibagi dengan jumlah data, yang sensitif terhadap nilai ekstrem.
- Modusadalah nilai yang paling sering muncul dalam suatu kumpulan data, yang tidak selalu merupakan nilai tengah.
Median lebih tahan terhadap nilai ekstrem daripada mean dan memberikan representasi yang lebih baik dari nilai tengah suatu kumpulan data yang tidak simetris atau mengandung pencilan.
Keterbatasan Median

Median, sebagai ukuran pemusatan data, memiliki keterbatasan tertentu yang perlu dipertimbangkan. Dalam beberapa kasus, median mungkin tidak secara akurat mewakili data atau memberikan wawasan yang memadai.
Kasus di Mana Median Tidak Akurat
- Data Sangat Asimetris:Ketika data memiliki distribusi yang sangat asimetris (skewed), median dapat ditarik ke arah ekor distribusi yang lebih panjang, sehingga tidak mencerminkan pusat data secara akurat.
- Outlier Ekstrem:Adanya outlier ekstrem dapat sangat memengaruhi median, terutama dalam kumpulan data yang kecil. Outlier dapat menarik median menjauh dari nilai yang lebih representatif.
- Data Ordinal:Median tidak sesuai untuk data ordinal, di mana urutan data penting tetapi perbedaan antar nilai tidak sama. Median dapat memberikan nilai tengah yang menyesatkan dalam kasus seperti itu.
Perbandingan dengan Ukuran Pemusatan Lainnya
Median dapat dibandingkan dengan ukuran pemusatan lainnya, seperti mean dan modus, untuk memberikan pemahaman yang lebih komprehensif tentang data.
Median dari data pada tabel berikut adalah nilai tengah yang membagi data menjadi dua bagian yang sama. Median ini dapat digunakan untuk menganalisis tren dan pola dalam data, serta membandingkannya dengan data lain. Dalam konteks wirausaha di bidang kerajinan yang sukses wirausaha di bidang kerajinan yang sukses , median dapat digunakan untuk mengidentifikasi kisaran pendapatan atau profitabilitas yang khas, sehingga dapat membantu para wirausahawan dalam menetapkan tujuan dan strategi bisnis mereka.
Median dari data pada tabel berikut adalah ukuran statistik yang berharga untuk memahami distribusi data dan membuat keputusan berdasarkan data.
- Mean:Mean, atau rata-rata, memperhitungkan semua nilai data dan dapat dipengaruhi oleh outlier. Namun, mean memberikan ukuran pusat yang lebih stabil untuk data yang terdistribusi normal.
- Modus:Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Modus dapat memberikan wawasan tentang nilai yang paling umum, tetapi tidak selalu mewakili pusat data.
Pemilihan ukuran pemusatan yang tepat bergantung pada sifat data dan tujuan analisis. Median berguna ketika data asimetris atau berisi outlier, sedangkan mean lebih sesuai untuk data yang terdistribusi normal. Modus dapat melengkapi median dan mean dengan memberikan informasi tentang nilai yang paling sering muncul.
Penutupan Akhir
Median adalah ukuran pemusatan data yang kuat dan serbaguna yang banyak digunakan dalam berbagai bidang. Meskipun memiliki keterbatasan, median memberikan representasi data yang andal dan intuitif, terutama dalam kasus data miring. Memahami median sangat penting untuk interpretasi data yang akurat dan pengambilan keputusan yang tepat.
Bagian Pertanyaan Umum (FAQ)
Apa itu median?
Median adalah nilai tengah dalam sekumpulan data yang diurutkan.
Bagaimana cara menghitung median?
Urutkan data, tentukan titik tengah, dan ambil nilai pada titik tersebut (jika ganjil) atau rata-rata dua nilai tengah (jika genap).