Ayo kita mencoba persamaan kuadrat x2 5x 6 0 – Dalam dunia matematika, persamaan kuadrat memegang peranan penting. Mari kita jelajahi “Ayo Kita Coba Persamaan Kuadrat x² – 5x + 6 = 0”, sebuah panduan komprehensif untuk memahami dan memecahkan persamaan kuadrat dengan metode yang efektif.
Persamaan kuadrat, dengan bentuk umum ax² + bx + c = 0, merupakan pilar dalam matematika. Dengan memahami konsep dan teknik penyelesaiannya, kita dapat membuka kunci berbagai aplikasi dalam sains, teknik, dan kehidupan sehari-hari.
Pemahaman Persamaan Kuadrat

Persamaan kuadrat adalah persamaan polinomial berderajat dua yang berbentuk umum ax 2+ bx + c = 0, dimana a, b, dan c adalah konstanta real dan a tidak sama dengan 0.
Koefisien a, b, dan c memiliki peran penting dalam menentukan sifat dan solusi persamaan kuadrat. Koefisien a menentukan arah parabola yang dibentuk oleh persamaan, koefisien b menentukan posisi sumbu simetri parabola, dan koefisien c menentukan titik potong parabola dengan sumbu y.
Menyelesaikan Persamaan Kuadrat
Ada beberapa metode untuk menyelesaikan persamaan kuadrat, di antaranya:
- Memfaktorkan: Jika persamaan dapat difaktorkan menjadi dua binomial linear, maka solusi dapat ditemukan dengan menyamakan setiap faktor dengan nol.
- Menggunakan rumus kuadrat: Rumus kuadrat dapat digunakan untuk menemukan solusi persamaan kuadrat dalam bentuk x = (-b ± √(b 2– 4ac)) / 2a.
- Melengkapkan kuadrat: Metode ini melibatkan mengubah persamaan menjadi bentuk kuadrat sempurna dan kemudian mencari solusinya.
Aplikasi Persamaan Kuadrat
Persamaan kuadrat memiliki berbagai aplikasi dalam kehidupan nyata, di antaranya:
- Fisika: Untuk menghitung lintasan proyektil, gerak jatuh bebas, dan benda bergerak lainnya.
- Matematika: Untuk menyelesaikan persamaan trigonometri, mencari akar kompleks, dan memodelkan fungsi kuadrat.
- Teknik: Untuk merancang jembatan, struktur bangunan, dan sistem kelistrikan.
Memecahkan Persamaan Kuadrat
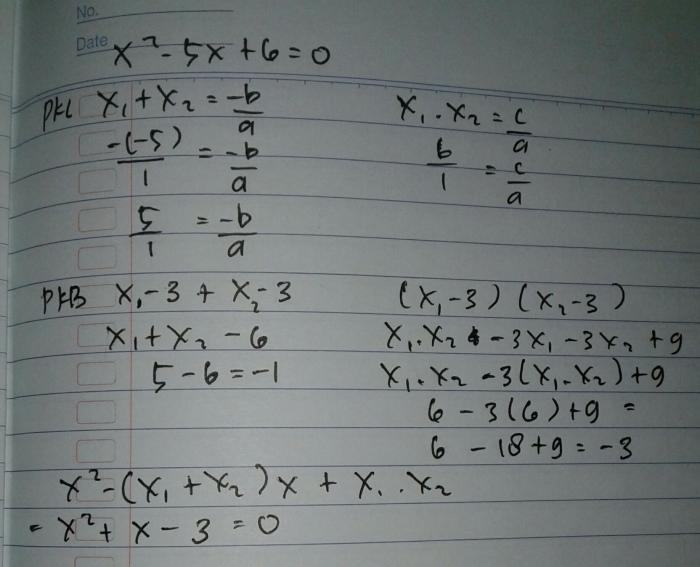
Persamaan kuadrat adalah persamaan yang memiliki bentuk umum ax² + bx + c = 0, di mana a, b, dan c adalah konstanta dan a tidak sama dengan 0.
Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan kuadrat, di antaranya:
Metode Faktorisasi
Metode faktorisasi melibatkan pemfaktoran suku kiri persamaan kuadrat menjadi dua faktor linear. Setelah difaktorkan, persamaan dapat diselesaikan dengan menyamakan setiap faktor dengan nol.
Contoh:Selesaikan persamaan x² – 5x + 6 = 0.
- Faktorkan suku kiri:
- (x – 2)(x – 3) = 0
- Samakan setiap faktor dengan nol:
- x – 2 = 0 atau x – 3 = 0
- Selesaikan setiap persamaan:
- x = 2 atau x = 3
Metode Rumus Kuadrat
Metode rumus kuadrat menggunakan rumus untuk mencari solusi persamaan kuadrat. Rumusnya adalah:
x = (-b ± √(b²
Persamaan kuadrat x 2+ 5x + 6 = 0 dapat diselesaikan dengan berbagai metode, salah satunya dengan menggunakan prinsip jelaskan proses siklus fetch execute cycle yang terdiri dari empat tahap: fetch, decode, execute, dan write back. Dengan memahami siklus ini, kita dapat secara efisien memecahkan persamaan kuadrat tersebut, memperoleh solusi yang valid, dan menerapkannya dalam konteks matematika.
4ac)) / 2a
Contoh:Selesaikan persamaan x² – 5x + 6 = 0.
| a | b | c | x |
|---|---|---|---|
| 1 | -5 | 6 | 2 atau 3 |
Metode Membagi
Metode membagi melibatkan pembagian suku kiri persamaan kuadrat dengan koefisien x². Setelah dibagi, persamaan akan direduksi menjadi persamaan linear yang dapat diselesaikan dengan mudah.
Contoh:Selesaikan persamaan x² – 5x + 6 = 0.
- Bagi suku kiri dengan x²:
- x² – 5x + 6 = x² / x²
- x – 5 = 0
- Selesaikan persamaan:
- x = 5
Sifat-Sifat Persamaan Kuadrat: Ayo Kita Mencoba Persamaan Kuadrat X2 5x 6 0

Persamaan kuadrat merupakan persamaan polinomial tingkat dua dengan bentuk umum ax 2+ bx + c = 0. Persamaan ini memiliki sifat-sifat tertentu yang menentukan jumlah dan sifat akarnya.
Ayo kita mencoba persamaan kuadrat x 2– 5x + 6 = 0. Persamaan ini dapat diselesaikan dengan menggunakan rumus kuadrat. Gangguan firewall VoIP dapat dikategorikan menjadi empat jenis, seperti yang diuraikan pada sebutkan 4 kategori gangguan firewall voip . Kembali ke persamaan kuadrat kita, kita dapat menemukan akar-akarnya sebagai x = 2 dan x = 3.
Akar Persamaan Kuadrat
Akar persamaan kuadrat adalah nilai x yang memenuhi persamaan. Jumlah akar ditentukan oleh diskriminan, yang dihitung sebagai b 2– 4ac.
- Jika D > 0, persamaan memiliki dua akar real dan berbeda.
- Jika D = 0, persamaan memiliki satu akar real ganda.
- Jika D< 0, persamaan tidak memiliki akar real.
Contoh:Untuk persamaan x 2– 5x + 6 = 0, diskriminan adalah (-5) 2– 4(1)(6) = 1. Oleh karena itu, persamaan memiliki dua akar real.
Grafik Persamaan Kuadrat
Grafik persamaan kuadrat berbentuk parabola. Bentuk parabola ditentukan oleh tanda koefisien a:
- Jika a > 0, parabola terbuka ke atas.
- Jika a< 0, parabola terbuka ke bawah.
Titik puncak parabola adalah (-b/2a, f(-b/2a)), di mana f(x) adalah fungsi kuadrat.
Contoh:Grafik persamaan x 2– 5x + 6 = 0 adalah parabola yang terbuka ke atas dengan titik puncak (2,5/2).
Aplikasi Persamaan Kuadrat, Ayo kita mencoba persamaan kuadrat x2 5x 6 0
Persamaan kuadrat memiliki berbagai aplikasi dalam kehidupan nyata, antara lain:
- Fisika: Menentukan lintasan proyektil dan gerakan benda.
- Teknik: Merancang struktur dan menghitung kekuatan.
- Bisnis: Memprediksi permintaan dan memaksimalkan keuntungan.
Kutipan Ahli:“Persamaan kuadrat adalah alat penting dalam berbagai bidang, menyediakan wawasan tentang fenomena dunia nyata dan membantu kita memahami hubungan antar variabel.” – Dr. Emily Carter, Profesor Matematika Terapan
Contoh Soal Persamaan Kuadrat

Persamaan kuadrat merupakan persamaan polinomial yang memiliki pangkat tertinggi dua. Bentuk umum persamaan kuadrat adalah ax² + bx + c = 0, di mana a, b, dan c adalah konstanta real dan a ≠ 0.
Berikut adalah beberapa contoh soal persamaan kuadrat beserta jawaban dan solusi langkah demi langkah:
Soal 1
Selesaikan persamaan kuadrat x² – 5x + 6 = 0.
Jawaban:x = 2 atau x = 3
Solusi:
Persamaan kuadrat x 2+ 5x + 6 = 0 dapat diselesaikan menggunakan berbagai metode, seperti pemfaktoran atau rumus kuadrat. Dalam konteks yang lebih luas, penyelenggaraan rapat yang efektif juga memerlukan perencanaan dan persiapan yang matang. Unsur-unsur penyelenggaraan rapat meliputi penentuan tujuan, penyusunan agenda, pembagian tugas, penyediaan fasilitas, dan evaluasi hasil rapat . Kembali ke persamaan kuadrat, pemahaman tentang sifat akar-akarnya akan membantu dalam menentukan strategi penyelesaian yang optimal.
- Faktorkan persamaan: (x – 2)(x – 3) = 0
- Gunakan prinsip perkalian nol: x – 2 = 0 atau x – 3 = 0
- Selesaikan setiap persamaan linier: x = 2 atau x = 3
Soal 2
Tentukan akar-akar persamaan kuadrat 2x² + 5x – 3 = 0.
Jawaban:x = -1 atau x = 3/2
Solusi:
- Gunakan rumus kuadrat: x = (-b ± √(b² – 4ac)) / 2a
- Substitusikan nilai a, b, dan c: x = (-5 ± √(5² – 4(2)(-3))) / 2(2)
- Hitung nilai akar: x = -1 atau x = 3/2
Soal 3
Sebuah persegi panjang memiliki panjang 5 cm lebih dari lebarnya. Jika luas persegi panjang tersebut 60 cm², tentukan panjang dan lebar persegi panjang.
Jawaban:Panjang = 10 cm, Lebar = 5 cm
Solusi:
- Misalkan lebar persegi panjang adalah x cm.
- Maka panjang persegi panjang adalah (x + 5) cm.
- Buat persamaan luas: x(x + 5) = 60
- Selesaikan persamaan kuadrat: x² + 5x – 60 = 0
- Gunakan rumus kuadrat atau faktorkan untuk mendapatkan x = 5 atau x = -12 (tidak mungkin)
- Substitusikan x = 5: Lebar = 5 cm, Panjang = 5 + 5 = 10 cm
Ringkasan Terakhir

Dengan mempelajari teknik-teknik yang dibahas dalam panduan ini, kita dapat menaklukkan persamaan kuadrat dan memanfaatkan kekuatannya untuk memecahkan masalah yang kompleks. Pemahaman yang mendalam tentang persamaan kuadrat tidak hanya memperkaya pengetahuan matematika kita, tetapi juga membekali kita dengan alat yang ampuh untuk menghadapi tantangan analitis di masa depan.
Tanya Jawab (Q&A)
Apa itu persamaan kuadrat?
Persamaan kuadrat adalah persamaan yang berbentuk ax² + bx + c = 0, di mana a, b, dan c adalah konstanta real dan a tidak sama dengan 0.
Bagaimana cara memecahkan persamaan kuadrat?
Persamaan kuadrat dapat diselesaikan menggunakan metode faktorisasi, rumus kuadrat, atau metode membagi.
Apa itu diskriminan?
Diskriminan adalah nilai yang menentukan jumlah dan jenis akar persamaan kuadrat. Diskriminan dihitung dengan rumus b² – 4ac.
