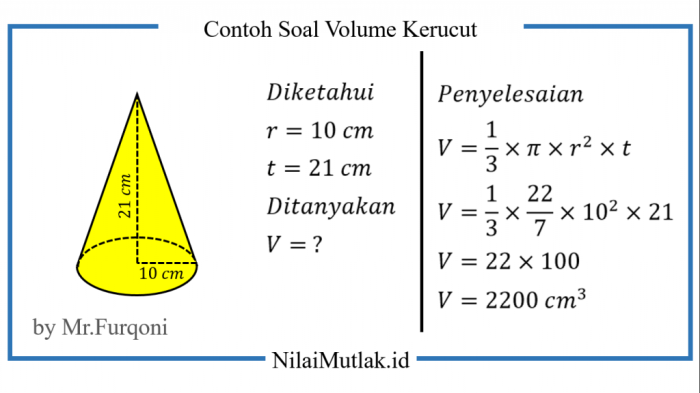
Dalam geometri, kerucut adalah bangun ruang tiga dimensi yang terbentuk dari titik puncak yang dihubungkan dengan setiap titik pada lingkaran di bidang yang disebut alas. Salah satu karakteristik penting dari kerucut adalah sisi miringnya, yang merupakan jarak dari titik puncak ke setiap titik pada alas.
Rumus sisi miring kerucut memainkan peran penting dalam menghitung ukuran dan sifat kerucut.
Artikel ini memberikan panduan komprehensif tentang rumus sisi miring kerucut, termasuk definisi, bukti, penerapan, variasi, dan rumus terkait lainnya. Dengan pemahaman yang jelas tentang rumus ini, Anda dapat dengan mudah menyelesaikan berbagai masalah geometri yang melibatkan kerucut.
Definisi Kerucut
Kerucut adalah bangun ruang tiga dimensi yang memiliki alas berbentuk lingkaran dan satu sisi melengkung yang menyatu pada satu titik yang disebut titik puncak. Tinggi kerucut adalah jarak antara titik puncak dan pusat alas, sedangkan garis pelukis adalah ruas garis dari titik puncak ke suatu titik pada keliling alas.
Ilustrasi Kerucut
[Deskripsikan ilustrasi kerucut yang memperlihatkan alas, tinggi, dan garis pelukis.]
Rumus Sisi Miring Kerucut
Dalam geometri, kerucut adalah bangun ruang tiga dimensi yang memiliki alas berbentuk lingkaran dan sebuah titik puncak. Sisi miring kerucut adalah garis lurus yang menghubungkan titik puncak dengan keliling alas.
Rumus Sisi Miring Kerucut
Rumus untuk menghitung sisi miring (s) kerucut adalah:
s = √(r² + h²)
di mana:* r adalah jari-jari alas kerucut
h adalah tinggi kerucut
Contoh Penggunaan Rumus
Misalkan sebuah kerucut memiliki jari-jari alas 5 cm dan tinggi 12 cm. Maka sisi miring kerucut tersebut dapat dihitung sebagai berikut:
s = √(5² + 12²)s = √(25 + 144)s = √169s = 13 cm
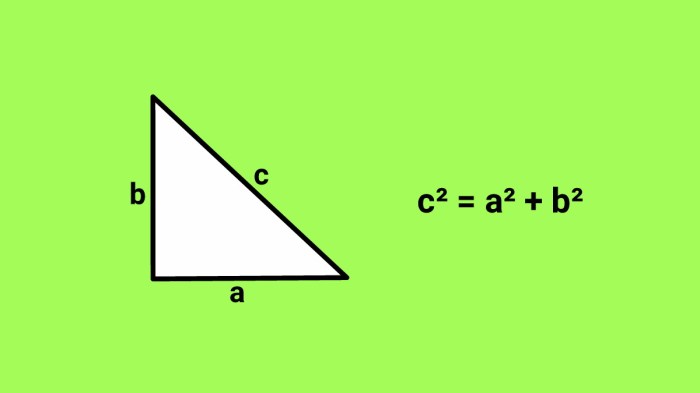
Bukti Rumus Sisi Miring Kerucut
Rumus sisi miring kerucut dapat dibuktikan menggunakan Teorema Pythagoras.
Langkah-langkah Pembuktian
- Buat sebuah kerucut dengan jari-jari alas r, tinggi h, dan sisi miring s.
- Buat bidang datar yang melalui sumbu kerucut dan salah satu titik pada lingkaran alas.
- Bidang ini memotong sisi miring dan alas kerucut membentuk segitiga siku-siku dengan sisi miring s, sisi depan r, dan sisi tegak h.
- Terapkan Teorema Pythagoras pada segitiga siku-siku ini:
s 2 = r 2 + h 2
Dari persamaan ini, kita dapat memperoleh rumus sisi miring kerucut:
s = √( r 2 + h 2 )
Penerapan Rumus Sisi Miring Kerucut
Rumus sisi miring kerucut memiliki penerapan luas dalam berbagai bidang kehidupan nyata. Salah satu aplikasi umum adalah menghitung tinggi benda berbentuk kerucut, seperti kerucut es krim.
Perhitungan Tinggi Kerucut Es Krim
Untuk menghitung tinggi kerucut es krim, kita dapat menggunakan rumus sisi miring kerucut, di mana sisi miring adalah jarak dari puncak kerucut ke tepi alasnya, dan jari-jari alas adalah setengah dari diameter alas.
Misalnya, jika kerucut es krim memiliki jari-jari alas 3 cm dan sisi miring 5 cm, maka tingginya dapat dihitung sebagai:
tinggi = √(sisi miring²
jari-jari alas²)
tinggi = √(5²
3²)
tinggi = √(25
9)
tinggi = √16
tinggi = 4 cm
Variasi Rumus Sisi Miring Kerucut
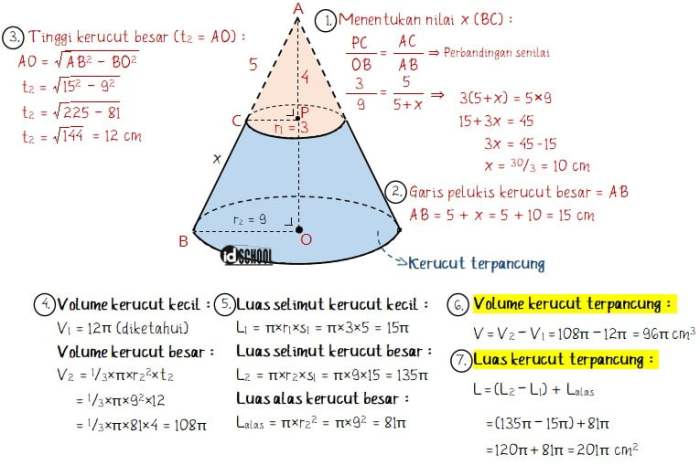
Rumus sisi miring kerucut yang telah dibahas sebelumnya dapat bervariasi untuk kasus-kasus khusus, seperti kerucut terpancung atau kerucut miring.
Kerucut Terpancung
Kerucut terpancung adalah kerucut yang bagian puncaknya terpotong oleh bidang datar sejajar dengan alasnya. Untuk menghitung sisi miring kerucut terpancung, digunakan rumus berikut:
s = √(r² + h² – R²) + √(R² + H² – r²)
di mana:
- s adalah sisi miring
- r adalah jari-jari alas bawah
- R adalah jari-jari alas atas
- h adalah tinggi kerucut terpancung dari alas bawah
- H adalah tinggi kerucut terpancung dari alas atas
Kerucut Miring
Kerucut miring adalah kerucut yang alasnya tidak tegak lurus dengan sumbu kerucut. Untuk menghitung sisi miring kerucut miring, digunakan rumus berikut:
s = √(r² + h² – r² cos²α)
di mana:
- s adalah sisi miring
- r adalah jari-jari alas
- h adalah tinggi kerucut
- α adalah sudut antara sumbu kerucut dan alas
Contoh Soal
Sebuah kerucut terpancung memiliki jari-jari alas bawah 6 cm, jari-jari alas atas 4 cm, dan tinggi 10 cm. Hitunglah sisi miring kerucut terpancung tersebut.
Penyelesaian:
Menggunakan rumus untuk kerucut terpancung:
s = √(6² + 10² – 4²) + √(4² + 10² – 6²)
s = √(36 + 100 – 16) + √(16 + 100 – 36)
s = √120 + √80
s ≈ 12,73 cm
Rumus Terkait Kerucut Lainnya
Selain rumus sisi miring kerucut, terdapat beberapa rumus lain yang terkait dengan kerucut, seperti volume, luas permukaan, dan luas alas.
Berikut adalah tabel yang merangkum rumus-rumus tersebut:
| Rumus | Penjelasan |
|---|---|
| V = (1/3)πr²h | Volume kerucut, di mana V adalah volume, r adalah jari-jari alas, dan h adalah tinggi kerucut |
| A = πr(r + s) | Luas permukaan kerucut, di mana A adalah luas permukaan, r adalah jari-jari alas, dan s adalah sisi miring kerucut |
| Aalas = πr² | Luas alas kerucut, di mana Aalas adalah luas alas dan r adalah jari-jari alas |
Ringkasan Penutup

Kesimpulannya, rumus sisi miring kerucut adalah alat penting dalam geometri yang memungkinkan kita menghitung sisi miring kerucut dengan akurat. Pemahaman yang baik tentang rumus ini sangat penting untuk menyelesaikan masalah yang melibatkan kerucut dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Dengan menerapkan prinsip-prinsip yang diuraikan dalam artikel ini, Anda dapat memperoleh pemahaman yang komprehensif tentang rumus sisi miring kerucut dan penerapannya dalam kehidupan nyata.
Tanya Jawab (Q&A)
Apa itu kerucut?
Kerucut adalah bangun ruang tiga dimensi yang terbentuk dari titik puncak yang dihubungkan dengan setiap titik pada lingkaran di bidang yang disebut alas.
Apa rumus sisi miring kerucut?
Rumus sisi miring kerucut adalah s = √(r² + h²), di mana s adalah sisi miring, r adalah jari-jari alas, dan h adalah tinggi kerucut.
Bagaimana cara membuktikan rumus sisi miring kerucut?
Rumus sisi miring kerucut dapat dibuktikan menggunakan Teorema Pythagoras.
Apa saja penerapan rumus sisi miring kerucut?
Rumus sisi miring kerucut digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan desain, untuk menghitung ukuran dan sifat kerucut.
Apa saja variasi rumus sisi miring kerucut?
Ada variasi rumus sisi miring kerucut untuk kasus-kasus khusus, seperti kerucut terpancung atau kerucut miring.