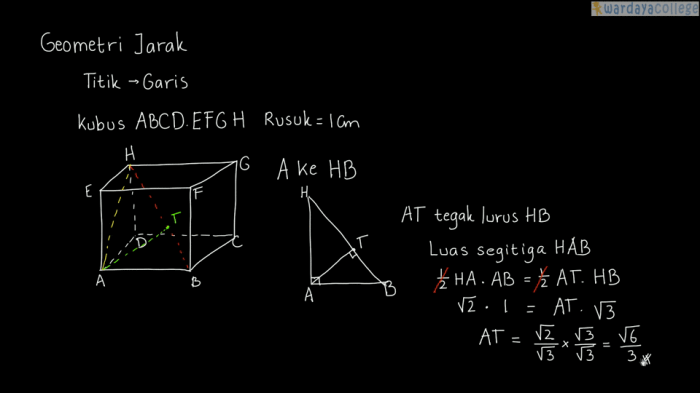
Dalam geometri dan aplikasi praktis, konsep jarak titik ke titik memegang peranan penting. Jarak ini mengukur jarak antara dua titik dalam ruang dan memiliki beragam aplikasi dalam kehidupan sehari-hari, teknik, sains, dan navigasi.
Pemahaman tentang soal jarak titik ke titik sangat penting untuk memecahkan masalah dan membuat keputusan yang akurat dalam berbagai bidang. Artikel ini akan membahas konsep dasar, aplikasi, metode penghitungan, dan algoritma yang terkait dengan soal jarak titik ke titik.
Konsep Jarak Titik ke Titik

Jarak titik ke titik adalah ukuran jarak antara dua titik dalam suatu ruang. Dalam bidang Cartesian, jarak antara dua titik dapat dihitung menggunakan rumus jarak berikut:
d = √((x2
- x1)² + (y2
- y1)²)
di mana (x1, y1) dan (x2, y2) adalah koordinat kedua titik tersebut.
Contoh Perhitungan Jarak Titik ke Titik
Misalkan kita ingin menghitung jarak antara titik A(2, 3) dan B(5, 7). Menggunakan rumus jarak, kita dapat menghitung:
d = √((5
- 2)² + (7
- 3)²) = √(3² + 4²) = √(9 + 16) = √25 = 5
Jadi, jarak antara titik A dan B adalah 5 satuan.
Aplikasi Jarak Titik ke Titik
Jarak titik ke titik adalah ukuran jarak antara dua titik dalam suatu ruang. Aplikasi jarak titik ke titik sangat luas dalam berbagai bidang kehidupan.
Kehidupan Sehari-hari
* Penentuan jarak tempuh perjalanan menggunakan aplikasi navigasi.
- Pengukuran jarak antar kota untuk perencanaan perjalanan.
- Estimasi jarak antar toko atau tempat umum untuk efisiensi waktu.
Teknik dan Sains
* Perhitungan jarak antara molekul dalam simulasi kimia.
- Pengukuran jarak antar benda langit dalam astronomi.
- Analisis pola dalam data spasial menggunakan algoritma berbasis jarak.
Sistem Navigasi
* Perhitungan jarak terpendek antara dua titik pada peta.
- Pemberian petunjuk arah yang akurat berdasarkan jarak ke tujuan.
- Penentuan waktu tempuh perjalanan dengan mempertimbangkan jarak dan kondisi lalu lintas.
Cara Menghitung Jarak Titik ke Titik
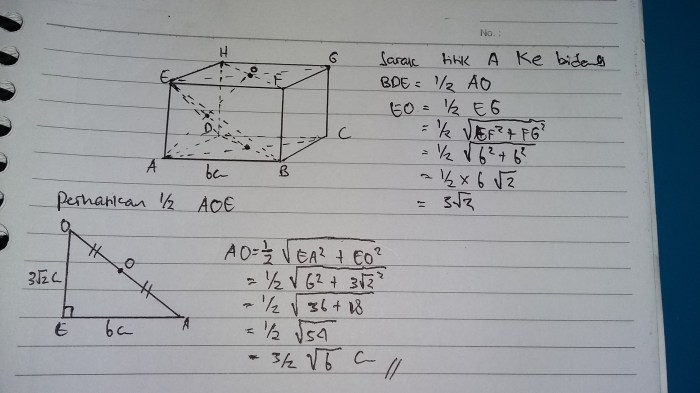
Menghitung jarak titik ke titik adalah tugas penting dalam berbagai aplikasi, seperti geometri, navigasi, dan fisika. Memahami cara menghitung jarak ini sangat penting untuk menyelesaikan masalah-masalah praktis.
Ada beberapa metode yang dapat digunakan untuk menghitung jarak titik ke titik. Salah satu metode yang paling umum digunakan adalah rumus jarak, yang memanfaatkan teorema Pythagoras.
Langkah-langkah Menghitung Jarak Titik ke Titik
- Tentukan koordinat kedua titik.
- Kurangkan koordinat x titik kedua dari koordinat x titik pertama untuk mendapatkan selisih x.
- Kurangkan koordinat y titik kedua dari koordinat y titik pertama untuk mendapatkan selisih y.
- Kuadratkan selisih x dan selisih y.
- Tambahkan hasil kuadrat dari langkah 4.
- Hitung akar kuadrat dari hasil langkah 5 untuk mendapatkan jarak titik ke titik.
Ilustrasi
Misalkan kita memiliki dua titik, A(2, 3) dan B(5, 7). Untuk menghitung jarak titik ke titik, kita dapat menggunakan langkah-langkah berikut:
- Selisih x: 5
2 = 3
- Selisih y: 7
3 = 4
- Kuadrat selisih x: 3^2 = 9
- Kuadrat selisih y: 4^2 = 16
- Jumlah kuadrat: 9 + 16 = 25
- Jarak titik ke titik: √25 = 5
Oleh karena itu, jarak antara titik A(2, 3) dan B(5, 7) adalah 5 satuan.
Sumber Daya Tambahan
- Khan Academy: Distance Between Two Points
- Math is Fun: Distance Between Two Points
- Wyzant: Distance Formula
Algoritma untuk Menghitung Jarak Titik ke Titik
Menghitung jarak titik ke titik adalah tugas umum dalam geometri dan memiliki berbagai aplikasi dalam ilmu komputer dan bidang lainnya. Ada beberapa algoritma yang dapat digunakan untuk menghitung jarak ini, masing-masing dengan efisiensi dan akurasi yang berbeda.
Algoritma Jarak Euclidean
Algoritma Jarak Euclidean adalah metode paling sederhana untuk menghitung jarak antara dua titik. Algoritma ini didasarkan pada teorema Pythagoras dan menghitung jarak sebagai akar kuadrat dari jumlah kuadrat selisih koordinat kedua titik.
“`jarak = sqrt((x2
- x1)^2 + (y2
- y1)^2)
“`
Algoritma Jarak Manhattan
Algoritma Jarak Manhattan menghitung jarak antara dua titik sebagai jumlah perbedaan absolut koordinat mereka. Algoritma ini lebih efisien daripada Jarak Euclidean karena tidak memerlukan operasi akar kuadrat.
“`jarak = abs(x2
- x1) + abs(y2
- y1)
“`
Algoritma Jarak Chebyshev
Algoritma Jarak Chebyshev menghitung jarak antara dua titik sebagai perbedaan maksimum antara koordinat mereka. Algoritma ini kurang akurat dibandingkan Jarak Euclidean tetapi lebih efisien.
“`jarak = max(abs(x2
- x1), abs(y2
- y1))
“`
Perbandingan Algoritma
Tabel berikut membandingkan efisiensi dan akurasi dari algoritma yang dibahas:
| Algoritma | Efisiensi | Akurasi |
|---|---|---|
| Jarak Euclidean | O(1) | Tinggi |
| Jarak Manhattan | O(1) | Sedang |
| Jarak Chebyshev | O(1) | Rendah |
Aplikasi Praktis
Algoritma untuk menghitung jarak titik ke titik memiliki banyak aplikasi praktis, seperti:
- Menemukan titik terdekat dalam kumpulan data
- Membuat grafik dan visualisasi data
- Menghitung jarak antar objek dalam aplikasi game
Kesimpulan Akhir

Dengan memahami konsep dan teknik soal jarak titik ke titik, kita dapat menyelesaikan masalah geometri yang kompleks, merancang sistem navigasi yang efisien, dan melakukan perhitungan akurat dalam berbagai bidang aplikasi. Pemahaman yang mendalam tentang topik ini sangat penting untuk pengembangan solusi inovatif dan kemajuan teknologi di masa depan.
Bagian Pertanyaan Umum (FAQ)
Apa rumus jarak titik ke titik dalam bidang Cartesian?
d = √[(x2 – x1)² + (y2 – y1)²]
Sebutkan tiga aplikasi soal jarak titik ke titik dalam kehidupan sehari-hari.
– Menentukan jarak mengemudi
– Mencari lokasi objek pada peta
– Merancang tata letak ruangan