Dalam ranah desain rangkaian digital, tabel kebenaran full adder memegang peranan penting sebagai fondasi untuk merancang rangkaian penjumlah biner. Full adder, sebuah komponen vital dalam unit aritmatika dan logika (ALU), melakukan operasi penjumlahan pada bilangan biner satu bit, membentuk dasar bagi operasi aritmatika yang lebih kompleks.
Artikel ini akan mengeksplorasi tabel kebenaran full adder, menyelidiki implementasinya, aplikasinya, dan representasinya dalam logika Boolean. Dengan memahami konsep-konsep ini, perancang dapat memanfaatkan tabel kebenaran full adder secara efektif untuk menciptakan rangkaian digital yang andal dan efisien.
Pengertian Tabel Kebenaran Full Adder
Full adder adalah rangkaian logika digital yang melakukan penjumlahan biner tiga bilangan biner, yaitu dua bilangan input (A dan B) dan satu bilangan carry-in (Cin). Rangkaian ini menghasilkan dua output: jumlah (Sum) dan carry-out (Cout).
Tabel kebenaran full adder menunjukkan semua kemungkinan kombinasi input dan output. Tabel ini digunakan untuk merancang dan menganalisis rangkaian full adder.
Contoh Rangkaian Full Adder Sederhana
Salah satu implementasi sederhana dari full adder menggunakan gerbang logika AND, OR, dan XOR:
- Sum = A XOR B XOR Cin
- Cout = (A AND B) OR (A AND Cin) OR (B AND Cin)
Implementasi Tabel Kebenaran Full Adder
Full adder adalah rangkaian logika digital yang digunakan untuk menjumlahkan tiga bit biner, yaitu dua bit input dan satu bit carry. Tabel kebenaran digunakan untuk menentukan keluaran rangkaian untuk semua kombinasi input yang mungkin.
Membuat Tabel Kebenaran Full Adder
| A | B | Cin | Sum | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Dari tabel kebenaran, dapat diamati bahwa:
- Bit sum bernilai 1 jika ada jumlah bit input ganjil, termasuk bit carry.
- Bit carry bernilai 1 jika ada dua atau lebih bit input yang bernilai 1.
Merancang Rangkaian Full Adder Menggunakan Tabel Kebenaran
Tabel kebenaran dapat digunakan untuk merancang rangkaian full adder dengan menggunakan gerbang logika. Persamaan logika untuk bit sum dan carry adalah sebagai berikut:
Sum = A XOR B XOR CinCarry = (A AND B) OR (B AND Cin) OR (A AND Cin)
Persamaan ini dapat diimplementasikan menggunakan gerbang logika XOR, AND, dan OR.
Aplikasi Tabel Kebenaran Full Adder
Tabel kebenaran full adder berperan penting dalam desain rangkaian digital karena menyediakan dasar untuk memahami dan mengimplementasikan operasi penjumlahan biner.
Contoh Penggunaan dalam Desain Rangkaian Penjumlah Biner
Sebagai contoh, pertimbangkan rangkaian penjumlah biner yang dirancang untuk menjumlahkan dua bilangan biner 4-bit. Menggunakan tabel kebenaran full adder, insinyur dapat menentukan logika yang diperlukan untuk setiap bit dalam rangkaian.
Dengan memeriksa tabel kebenaran, mereka dapat menentukan bahwa untuk setiap kombinasi bit input (A, B, dan Cin), terdapat kombinasi output yang unik (Sum dan Cout). Informasi ini digunakan untuk membuat tabel logika yang mendefinisikan operasi rangkaian penjumlah.
Tabel logika kemudian digunakan untuk mendesain rangkaian gerbang logika yang mengimplementasikan operasi penjumlahan biner.
Tabel Kebenaran Full Adder yang Disederhanakan
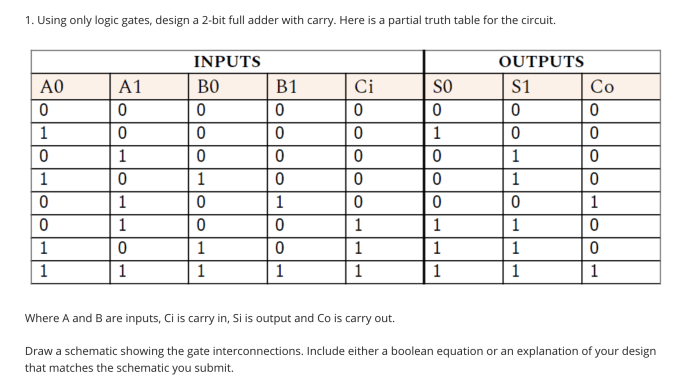
Tabel kebenaran full adder yang lengkap terdiri dari delapan baris, yang mewakili semua kemungkinan kombinasi input. Namun, dimungkinkan untuk menyederhanakan tabel kebenaran ini dengan mengidentifikasi pola dan menghapus baris yang berlebihan.
Identifikasi Pola
Dengan mengamati tabel kebenaran lengkap, kita dapat melihat bahwa ada beberapa pola yang dapat diidentifikasi:
- Jika kedua input (A dan B) adalah 0, maka output (Sum) selalu 0, terlepas dari nilai Carry-in (Cin).
- Jika salah satu input (A atau B) adalah 1 dan input lainnya adalah 0, maka output (Sum) adalah nilai Cin.
- Jika kedua input (A dan B) adalah 1, maka output (Sum) adalah Cin + 1, dan output (Carry-out) selalu 1.
Tabel Kebenaran yang Disederhanakan
Berdasarkan pola ini, kita dapat menyederhanakan tabel kebenaran full adder menjadi hanya empat baris, seperti yang ditunjukkan pada tabel berikut:
| A | B | Cin | Sum | Carry-out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
Tabel kebenaran yang disederhanakan ini hanya berisi baris-baris yang diperlukan untuk mewakili semua kemungkinan kombinasi input. Baris yang berlebihan, seperti baris yang mewakili kasus di mana A = 0 dan B = 0 (yang selalu menghasilkan Sum = 0), telah dihilangkan.
Keuntungan Menggunakan Tabel Kebenaran yang Disederhanakan
Menggunakan tabel kebenaran yang disederhanakan memiliki beberapa keuntungan, antara lain:
- Lebih mudah dibaca dan dipahami.
- Mempercepat proses desain dan analisis sirkuit.
- Membantu mengidentifikasi pola dan hubungan dalam sirkuit.
Tabel Kebenaran Full Adder dalam Logika Boolean
Full adder adalah rangkaian logika digital yang digunakan untuk menjumlahkan tiga bit biner (dua bit masukan dan satu bit carry-in). Tabel kebenaran full adder mencantumkan semua kemungkinan kombinasi input dan outputnya.
Ekspresi Persamaan Logika Boolean
Tabel kebenaran full adder dapat diekspresikan dalam bentuk persamaan logika Boolean sebagai berikut:
SUM = A XOR B XOR Cin
Cout = (A AND B) OR (A AND Cin) OR (B AND Cin)
Dimana:
- A dan B adalah bit masukan
- Cin adalah bit carry-in
- SUM adalah bit jumlah
- Cout adalah bit carry-out
Desain Rangkaian Full Adder
Persamaan-persamaan logika Boolean ini dapat digunakan untuk merancang rangkaian full adder. Rangkaian tersebut terdiri dari dua gerbang XOR (untuk menghitung SUM) dan tiga gerbang AND (untuk menghitung Cout).
Pemungkas
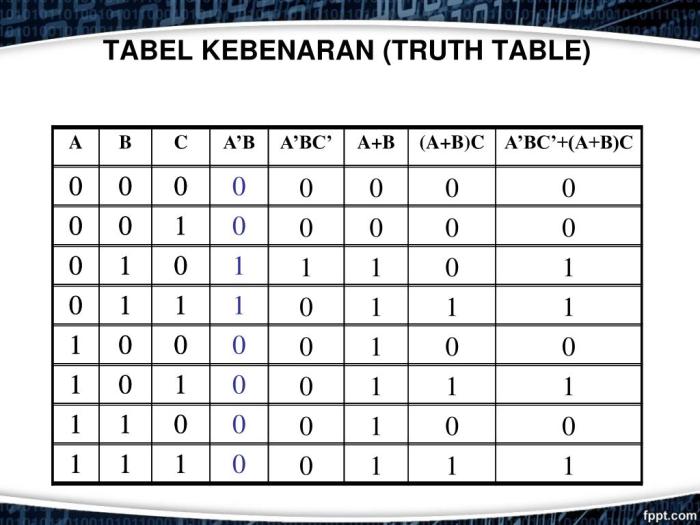
Tabel kebenaran full adder merupakan alat yang tak ternilai bagi perancang rangkaian digital, memberikan panduan yang komprehensif untuk membangun rangkaian penjumlah biner yang andal. Dengan memanfaatkan pola dan persamaan logika yang diuraikan dalam tabel ini, perancang dapat merancang rangkaian yang kompleks dengan percaya diri, membuka jalan bagi inovasi dalam komputasi dan teknologi.
Pertanyaan Umum yang Sering Muncul
Apa itu full adder?
Full adder adalah rangkaian logika digital yang melakukan operasi penjumlahan pada tiga bit input (dua bit angka dan satu bit carry-in) dan menghasilkan dua bit output (jumlah dan carry-out).
Bagaimana cara menggunakan tabel kebenaran full adder untuk merancang rangkaian?
Tabel kebenaran menyediakan kebenaran logis untuk semua kombinasi input yang mungkin. Perancang dapat menggunakan tabel ini untuk menentukan logika yang diperlukan untuk setiap output rangkaian, sehingga memfasilitasi proses desain.
Apa keuntungan menggunakan tabel kebenaran full adder yang disederhanakan?
Tabel kebenaran yang disederhanakan menghilangkan redundansi, menyoroti pola dan hubungan yang mendasarinya. Hal ini dapat menyederhanakan proses desain, mengurangi jumlah gerbang logika yang diperlukan, dan meningkatkan efisiensi rangkaian.
