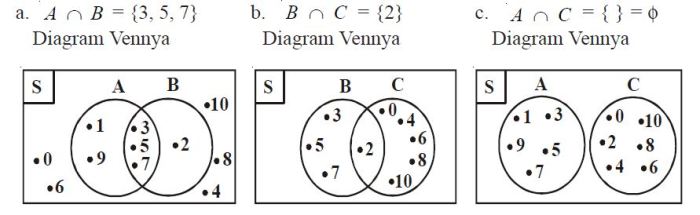
Dalam matematika, himpunan irisan memainkan peran penting dalam teori himpunan dan memiliki banyak aplikasi dalam berbagai bidang. Himpunan irisan mewakili sekumpulan elemen yang sama yang dimiliki oleh dua atau lebih himpunan.
Konsep himpunan irisan ini dapat dipahami dengan jelas melalui contoh soal yang akan dibahas secara mendalam dalam panduan ini. Dengan mempelajari contoh-contoh soal ini, kita dapat menguasai cara menentukan, memahami sifat-sifat, dan menerapkan himpunan irisan dalam kehidupan nyata.
Pengertian Himpunan Irisan
Himpunan irisan adalah himpunan yang memuat anggota-anggota yang sama dari dua himpunan atau lebih.
Dengan kata lain, himpunan irisan adalah hasil persekutuan dari dua himpunan atau lebih. Himpunan irisan dinotasikan dengan simbol ∩.
Contoh Himpunan Irisan
- Misalkan A = 1, 2, 3, 4, 5 dan B = 2, 4, 6, 8, 10. Maka himpunan irisan A dan B adalah 2, 4.
- Misalkan C = merah, kuning, hijau, biru dan D = biru, ungu, hijau, jingga. Maka himpunan irisan C dan D adalah biru, hijau.
Cara Menentukan Himpunan Irisan

Himpunan irisan adalah himpunan yang berisi elemen-elemen yang sama-sama terdapat dalam dua himpunan atau lebih. Untuk menentukan himpunan irisan, ikuti langkah-langkah berikut:
Langkah-langkah Menentukan Himpunan Irisan
- Tuliskan kedua himpunan yang akan dicari irisannya.
- Bandingkan elemen-elemen dari kedua himpunan.
- Tuliskan elemen-elemen yang sama-sama terdapat dalam kedua himpunan sebagai himpunan irisan.
Contoh
Tentukan himpunan irisan dari himpunan A = 1, 2, 3, 4 dan himpunan B = 3, 4, 5, 6.
Menuliskan kedua himpunan:
- A = 1, 2, 3, 4
- B = 3, 4, 5, 6
Membandingkan elemen-elemen:
- 1 ∈ A, tetapi 1 ∉ B
- 2 ∈ A, tetapi 2 ∉ B
- 3 ∈ A dan 3 ∈ B
- 4 ∈ A dan 4 ∈ B
- 5 ∈ B, tetapi 5 ∉ A
- 6 ∈ B, tetapi 6 ∉ A
Menuliskan himpunan irisan:
Himpunan irisan dari A dan B adalah 3, 4.
Sifat-Sifat Himpunan Irisan
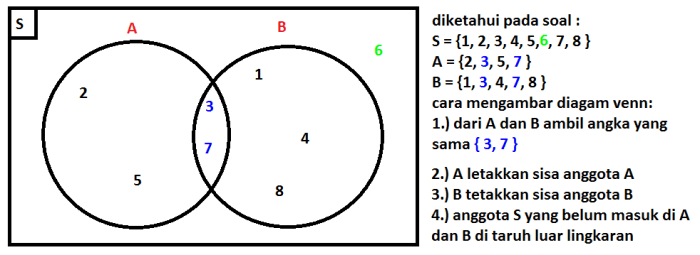
Himpunan irisan memiliki beberapa sifat penting yang dapat digunakan untuk mengoperasikan dan memanipulasinya. Sifat-sifat ini meliputi:
Sifat-Sifat Umum
- Sifat Komutatif: A ∩ B = B ∩ A
- Sifat Asosiatif: (A ∩ B) ∩ C = A ∩ (B ∩ C)
- Sifat Identitas: A ∩ U = A, A ∩ ∅ = ∅
- Sifat Absorbsi: A ∩ (A ∪ B) = A
Sifat Distributif
- Sifat Distributif terhadap Gabungan: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- Sifat Distributif terhadap Irisan: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Sifat-Sifat Tambahan
- Sifat Idempoten: A ∩ A = A
- Sifat Invers: A ∩ A’ = ∅
- Sifat Monotonisitas: Jika A ⊆ B, maka A ∩ C ⊆ B ∩ C
Sifat-sifat ini dapat digunakan untuk menyederhanakan operasi himpunan irisan dan memperoleh hasil yang diinginkan.
Contoh Soal Himpunan Irisan

Himpunan irisan adalah himpunan yang berisi anggota-anggota yang sama dari dua atau lebih himpunan. Berikut beberapa contoh soal himpunan irisan:
Mencari Himpunan Irisan
- Diketahui himpunan A = 1, 2, 3, 4, 5 dan B = 3, 4, 5, 6, 7. Tentukan himpunan irisan A dan B.
- Diketahui himpunan C = a, b, c, d dan D = c, d, e, f. Tentukan himpunan irisan C dan D.
Panduan Langkah Demi Langkah untuk Menyelesaikan Soal
- Identifikasi anggota-anggota yang sama dari kedua himpunan.
- Tuliskan anggota-anggota yang sama tersebut dalam tanda kurung kurawal .
Jawaban
- A ∩ B = 3, 4, 5
- C ∩ D = c, d
Penerapan Himpunan Irisan
Himpunan irisan memiliki banyak penerapan dalam kehidupan nyata. Ini digunakan di berbagai bidang, termasuk:
Ilmu Komputer
- Menggabungkan dua atau lebih set data untuk menemukan elemen yang sama.
- Menemukan kesamaan antara dua atau lebih program atau algoritma.
- Mendefinisikan batasan dan kondisi dalam bahasa pemrograman.
Matematika
- Menemukan solusi persamaan atau sistem persamaan.
- Membandingkan dua atau lebih himpunan untuk menentukan kesamaan atau perbedaan.
- Membuat model situasi dunia nyata menggunakan himpunan dan operasi irisan.
Statistika
- Menemukan persamaan dan perbedaan antara dua atau lebih kelompok data.
- Menentukan hubungan antara variabel yang berbeda.
- Membuat prediksi berdasarkan analisis data yang tumpang tindih.
Linguistik
- Menganalisis struktur dan arti kata atau frasa.
- Membandingkan dua atau lebih bahasa untuk menemukan kesamaan dan perbedaan.
- Mengembangkan sistem terjemahan bahasa.
Bisnis
- Menemukan target pasar yang tumpang tindih untuk beberapa produk atau layanan.
- Membandingkan kekuatan dan kelemahan pesaing.
- Menganalisis tren pasar dan membuat keputusan bisnis berdasarkan data yang tumpang tindih.
Penutup
Dengan memahami contoh soal himpunan irisan, kita memperoleh pemahaman yang komprehensif tentang konsep ini. Himpunan irisan memiliki aplikasi yang luas dalam berbagai bidang, seperti statistik, probabilitas, dan ilmu komputer. Menguasai contoh soal ini sangat penting untuk mengembangkan keterampilan analitis dan pemecahan masalah yang diperlukan dalam berbagai bidang studi dan profesi.
Jawaban untuk Pertanyaan Umum
Apa saja langkah-langkah untuk menentukan himpunan irisan?
Langkah-langkahnya adalah: 1) Menuliskan himpunan-himpunan yang akan dicari irisannya, 2) Mencari anggota yang sama dari himpunan-himpunan tersebut, 3) Menuliskan anggota-anggota yang sama tersebut dalam bentuk himpunan.
Apa sifat-sifat himpunan irisan?
Sifat-sifat himpunan irisan antara lain: komutatif, asosiatif, distributif terhadap irisan, dan distributif terhadap gabungan.
Bagaimana himpunan irisan digunakan dalam kehidupan nyata?
Himpunan irisan digunakan dalam berbagai bidang, seperti untuk menentukan kesamaan minat antara dua kelompok orang, menganalisis data statistik, dan merancang sistem komputer.