Dalam matematika, koordinat kutub menyediakan sistem alternatif untuk menentukan posisi suatu titik pada bidang. Sistem ini sangat berguna dalam bidang fisika, teknik, dan navigasi, karena memudahkan penggambaran besaran yang memiliki arah dan besar, seperti kecepatan dan posisi.
Dalam artikel ini, kita akan mengeksplorasi konsep koordinat kutub, rumus konversi, operasi, dan aplikasinya. Kita juga akan memecahkan contoh soal yang ilustratif untuk memperjelas konsep-konsep ini.
Definisi Koordinat Kutub
Koordinat kutub adalah sistem koordinat dua dimensi yang digunakan untuk menentukan lokasi suatu titik pada bidang datar. Sistem ini menggunakan jarak titik dari titik pusat (kutub) dan sudut antara garis yang menghubungkan titik tersebut dengan kutub dan sumbu horizontal (sumbu polar).
Ilustrasi Grafis
Sistem koordinat kutub digambarkan sebagai bidang datar dengan titik pusat (O) yang disebut kutub. Garis horizontal yang melewati kutub disebut sumbu polar (0°), dan garis-garis yang memancar dari kutub pada sudut tertentu disebut jari-jari.
Konversi Koordinat Kartesius ke Kutub

Dalam matematika, koordinat kutub adalah sistem koordinat dua dimensi yang menggunakan jarak dari titik asal dan sudut dari sumbu referensi untuk menentukan posisi titik.
Untuk mengonversi koordinat Kartesius (x, y) ke koordinat kutub (r, θ), gunakan rumus berikut:
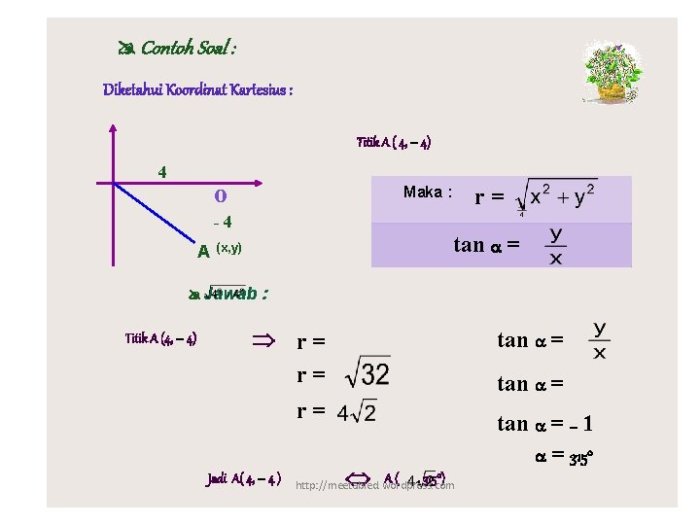
- Jarak (r): r = √(x² + y²)
- Sudut (θ): θ = arctan(y/x)
Contoh Soal Konversi
Konversi koordinat Kartesius (3, 4) ke koordinat kutub.
- Jarak (r): r = √(3² + 4²) = 5
- Sudut (θ): θ = arctan(4/3) ≈ 53,13°
Jadi, koordinat kutubnya adalah (5, 53,13°).
Tabel Konversi Nilai Umum
| Koordinat Kartesius (x, y) | Koordinat Kutub (r, θ) |
|---|---|
| (0, 0) | (0, 0°) |
| (1, 0) | (1, 0°) |
| (0, 1) | (1, 90°) |
| (-1, 0) | (1, 180°) |
(0,
|
(1, 270°) |
Konversi Koordinat Kutub ke Kartesius
Koordinat kutub adalah sistem koordinat dua dimensi yang menggunakan jarak dari titik asal (disebut radius) dan sudut dari sumbu horizontal (disebut sudut).
Koordinat Kartesius, di sisi lain, adalah sistem koordinat dua dimensi yang menggunakan jarak dari dua sumbu tegak lurus (disebut sumbu x dan y).
Konversi dari Koordinat Kutub ke Kartesius
Untuk mengonversi koordinat kutub (r, θ) ke koordinat Kartesius (x, y), kita menggunakan rumus berikut:
x = r cos(θ) y = r sin(θ)
Di mana:
- r adalah jarak dari titik asal
- θ adalah sudut dari sumbu horizontal
- x adalah koordinat x
- y adalah koordinat y
Misalnya, untuk mengonversi koordinat kutub (3, π/4) ke koordinat Kartesius, kita akan menggunakan rumus di atas:
x = 3 cos(π/4) = 3√2/2 y = 3 sin(π/4) = 3√2/2
Jadi, koordinat Kartesius dari (3, π/4) adalah (3√2/2, 3√2/2).
Operasi pada Koordinat Kutub
Koordinat kutub adalah sistem koordinat dua dimensi yang menggunakan jarak dari titik asal dan sudut dari sumbu x positif untuk menentukan lokasi suatu titik.
Beberapa operasi yang dapat dilakukan pada koordinat kutub meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan dan Pengurangan
Untuk menjumlahkan atau mengurangkan dua koordinat kutub, kita harus mengonversi keduanya menjadi bentuk persegi panjang (kartesius), melakukan operasi penjumlahan atau pengurangan, dan kemudian mengonversi hasilnya kembali ke koordinat kutub.
Misalnya, untuk menjumlahkan koordinat kutub (3, π/4) dan (2, π/3), kita akan mendapatkan:
(3, π/4) + (2, π/3) = (3cos(π/4) + 2cos(π/3), 3sin(π/4) + 2sin(π/3)) = (2,732, 2,598)
Perkalian dan Pembagian
Untuk mengalikan atau membagi dua koordinat kutub, kita cukup mengalikan atau membagi besarnya dan menjumlahkan atau mengurangkan sudutnya.
Misalnya, untuk mengalikan koordinat kutub (3, π/4) dengan 2, kita akan mendapatkan:
(3, π/4) = (2 × 3, π/4) = (6, π/4)
Dan untuk membagi koordinat kutub (3, π/4) dengan 2, kita akan mendapatkan:
(3, π/4) ÷ 2 = (3 ÷ 2, π/4) = (1,5, π/4)
Contoh Soal
Tentukan koordinat kutub dari titik (4, 3) pada bidang cartesius.
Penyelesaian:
Besarnya r = √(x^2 + y^2) = √(4^2 + 3^2) = 5
Sudut θ = arctan(y/x) = arctan(3/4) = 36,87°
Jadi, koordinat kutub dari titik (4, 3) adalah (5, 36,87°).
Aplikasi Koordinat Kutub
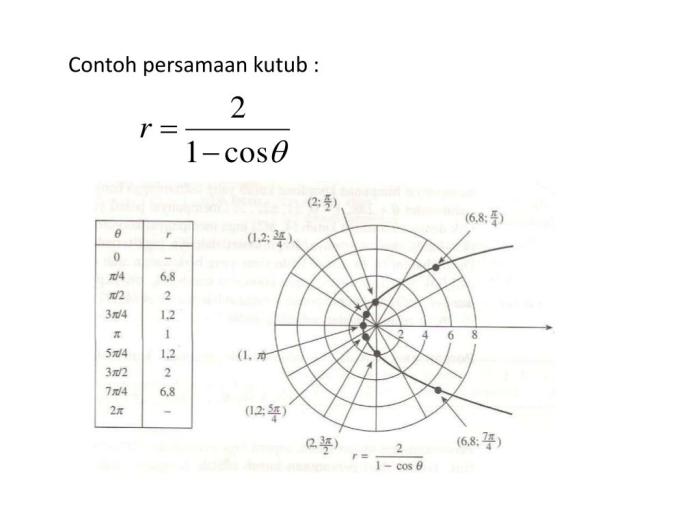
Koordinat kutub memiliki banyak aplikasi penting dalam berbagai bidang, termasuk fisika, teknik, dan navigasi. Sistem koordinat ini menawarkan cara yang efisien dan nyaman untuk mewakili titik dan vektor dalam ruang dua dimensi.
Fisika
Dalam fisika, koordinat kutub sering digunakan untuk menggambarkan gerakan melingkar dan getaran harmonik. Misalnya, posisi partikel yang bergerak melingkar dapat dinyatakan menggunakan koordinat kutub (r, θ), di mana r adalah jarak partikel dari pusat lingkaran dan θ adalah sudut yang dibuat oleh vektor posisi partikel terhadap sumbu x.
Teknik
Di bidang teknik, koordinat kutub digunakan untuk menganalisis dan merancang sistem mekanis yang melibatkan gerakan melingkar atau rotasi. Misalnya, koordinat kutub dapat digunakan untuk menghitung torsi dan gaya pada poros yang berputar atau untuk menganalisis gerakan robot yang memiliki sambungan putar.
Navigasi
Dalam navigasi, koordinat kutub digunakan untuk menentukan lokasi dan arah kapal atau pesawat. Latitude dan longitude, yang merupakan sistem koordinat geografis yang digunakan untuk menentukan lokasi di permukaan bumi, pada dasarnya adalah koordinat kutub. Latitude adalah sudut yang dibentuk oleh garis lintang dengan ekuator, sedangkan longitude adalah sudut yang dibentuk oleh garis bujur dengan meridian utama.
Terakhir

Koordinat kutub menawarkan representasi geometris yang kuat untuk besaran vektor. Pemahaman yang mendalam tentang koordinat kutub sangat penting untuk berbagai aplikasi di bidang sains, teknik, dan navigasi. Dengan menguasai konsep-konsep ini, kita dapat secara efektif menyelesaikan masalah dunia nyata yang melibatkan besaran vektor dan mengungkap pola yang tersembunyi dalam data.
Jawaban yang Berguna
Apa saja perbedaan utama antara koordinat kutub dan koordinat kartesius?
Koordinat kartesius menggunakan dua garis tegak lurus sebagai referensi, sedangkan koordinat kutub menggunakan titik pusat dan garis radial sebagai referensi. Koordinat kartesius lebih mudah digunakan untuk menggambarkan bentuk persegi panjang, sedangkan koordinat kutub lebih cocok untuk menggambarkan bentuk melingkar.
Bagaimana cara mengonversi koordinat kartesius ke koordinat kutub?
Gunakan rumus berikut: r = √(x² + y²) dan θ = arctan(y/x).
Apa saja aplikasi koordinat kutub dalam kehidupan nyata?
Koordinat kutub digunakan dalam navigasi untuk menentukan posisi kapal atau pesawat, dalam fisika untuk menganalisis gerakan melingkar, dan dalam teknik untuk merancang antena dan sirkuit.