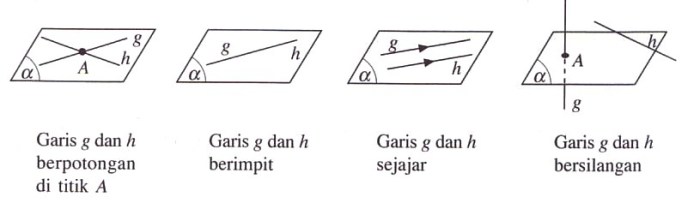
Dalam geometri, kedudukan garis pada bidang memainkan peran penting dalam menentukan hubungan spasial dan menyelesaikan masalah geometrik. Konsep ini melibatkan penentuan posisi relatif dua garis atau lebih dalam sebuah bidang datar.

Dengan memahami kedudukan garis, kita dapat memperoleh wawasan tentang sifat geometris suatu bangun, seperti segitiga, segi empat, dan lingkaran. Kedudukan garis juga memiliki aplikasi yang luas dalam bidang teknik, arsitektur, dan kehidupan sehari-hari.

Definisi Kedudukan Garis pada Bidang

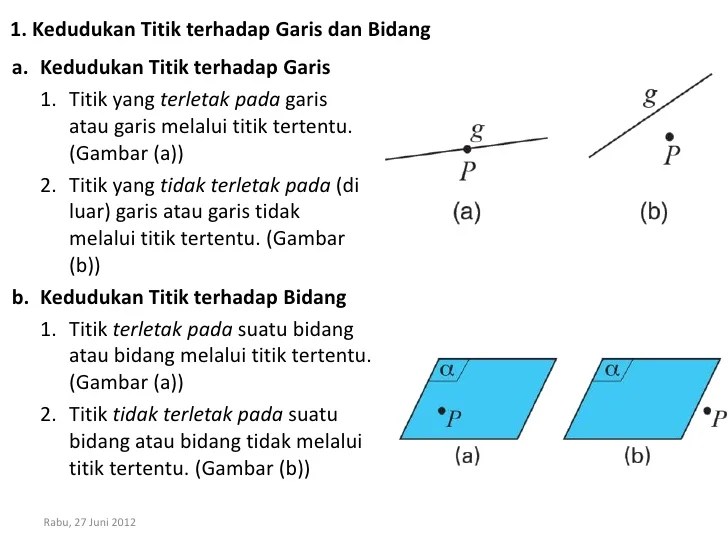
Kedudukan garis pada bidang adalah posisi relatif suatu garis terhadap garis lainnya pada bidang yang sama. Garis dapat berada pada posisi sejajar, tegak lurus, berpotongan, atau berimpit.

Berikut adalah ilustrasi contoh garis yang berada pada posisi berbeda pada bidang:

• Garis Sejajar: Dua garis yang tidak pernah berpotongan pada bidang yang sama, meskipun diperpanjang ke arah tak terhingga.
• Garis Tegak Lurus: Dua garis yang berpotongan pada sudut 90 derajat.
• Garis Berpotongan: Dua garis yang berpotongan pada suatu titik pada bidang yang sama.
• Garis Berimpit: Dua garis yang terletak pada titik yang sama pada bidang yang sama, sehingga keduanya merupakan garis yang sama.

Jenis-jenis Kedudukan Garis

Kedudukan garis pada bidang diklasifikasikan berdasarkan orientasi dan hubungannya dengan garis lain.

Berikut ini adalah jenis-jenis kedudukan garis pada bidang:

Sejajar

• Dua garis sejajar jika tidak berpotongan dan berada pada bidang yang sama.
• Garis sejajar memiliki gradien yang sama.

Tegak Lurus

• Dua garis tegak lurus jika membentuk sudut siku-siku (90°).
• Garis tegak lurus memiliki gradien yang saling invers dan negatif.

Sejajar dan Berimpit

• Dua garis sejajar dan berimpit jika berada pada bidang yang sama dan memiliki semua titik yang sama.
• Garis sejajar dan berimpit memiliki gradien dan persamaan yang sama.

Berpotongan

• Dua garis berpotongan jika berada pada bidang yang sama dan memiliki titik persekutuan.
• Gradien garis berpotongan tidak harus sama atau invers.

Skew

• Dua garis skew jika tidak berada pada bidang yang sama dan tidak memiliki titik persekutuan.
• Garis skew tidak memiliki gradien yang dapat dibandingkan.

Cara Menentukan Kedudukan Garis

Untuk menentukan kedudukan garis pada bidang, terdapat beberapa langkah yang dapat dilakukan:

Menentukan Gradien

Gradien garis (m) adalah perbandingan perubahan sumbu vertikal (Δy) terhadap perubahan sumbu horizontal (Δx) antara dua titik yang berbeda pada garis tersebut. Rumus gradien adalah:

m = Δy / Δx

Menentukan Persamaan Garis Bentuk Kemiringan-Potong

Persamaan garis bentuk kemiringan-potong adalah y = mx + c, di mana m adalah gradien dan c adalah titik potong sumbu y. Untuk menentukan persamaan ini, kita perlu mencari gradien dan titik potong sumbu y.

Menentukan Titik Potong Sumbu

Titik potong sumbu y adalah nilai y ketika x = 0. Untuk menentukannya, kita dapat mensubstitusikan x = 0 ke dalam persamaan garis bentuk kemiringan-potong:

c = y

Contoh Soal

Tentukan kedudukan garis yang melalui titik (2, 5) dan (4, 9).

Solusi:

1. Menentukan Gradien:

m = (9 – 5) / (4 – 2) = 4 / 2 = 2

2. Menentukan Persamaan Garis Bentuk Kemiringan-Potong:

y = 2x + c

3. Menentukan Titik Potong Sumbu Y:

c = 5 (karena ketika x = 0, y = 5)

4. Persamaan Garis:

y = 2x + 5

Aplikasi Kedudukan Garis dalam Geometri

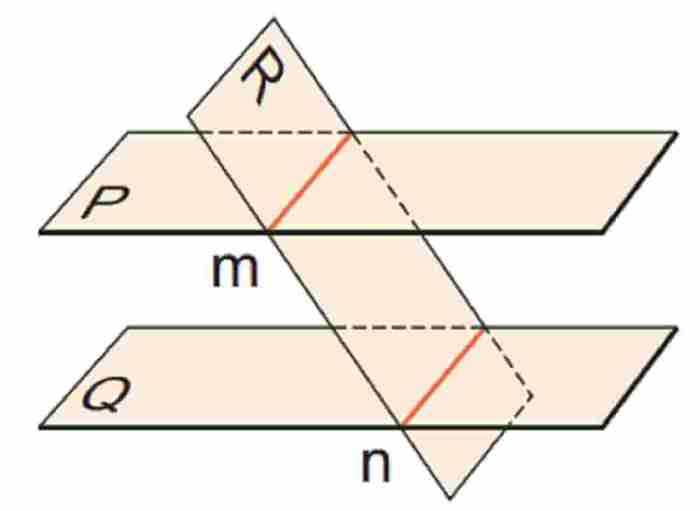
Kedudukan garis dalam geometri memiliki banyak aplikasi dalam menyelesaikan masalah dan membuktikan teorema. Salah satu aplikasinya adalah untuk menentukan apakah dua garis sejajar, berpotongan, atau tegak lurus.

Menentukan Kedudukan Garis

Untuk menentukan kedudukan dua garis, kita dapat menggunakan persamaan garis tersebut. Jika persamaan garis dalam bentuk kemiringan-perpotongan (y = mx + b), maka:* Jika dua garis memiliki kemiringan yang sama dan perpotongan y yang berbeda, maka garis-garis tersebut sejajar.

• Jika dua garis memiliki kemiringan yang berbeda, maka garis-garis tersebut berpotongan.
• Jika dua garis memiliki kemiringan 0 dan 1, maka garis-garis tersebut tegak lurus.

Contoh Soal

Misalkan kita memiliki dua garis dengan persamaan:* Garis 1: y = 2x + 1

Garis 2

y = 2x

3

Untuk menentukan kedudukan kedua garis, kita bandingkan kemiringan dan perpotongan y:* Kemiringan Garis 1: m1 = 2

Kemiringan Garis 2

m2 = 2

Perpotongan y Garis 1

b1 = 1

Perpotongan y Garis 2

b2 =

3

Karena m1 = m2 dan b1 ≠ b2, maka kedua garis sejajar.

Aplikasi Kedudukan Garis dalam Kehidupan Nyata

Kedudukan garis tidak hanya konsep teoretis tetapi juga memiliki banyak aplikasi praktis dalam berbagai bidang kehidupan.

Arsitektur

Dalam arsitektur, kedudukan garis digunakan untuk:

• Menentukan sudut dan jarak antar bangunan.
• Merancang fasad dan elemen struktural yang selaras.
• Memastikan kesimetrian dan keseimbangan dalam desain bangunan.

Teknik

Di bidang teknik, kedudukan garis berperan penting dalam:

• Desain jembatan dan struktur lainnya untuk memastikan stabilitas dan keamanan.
• Pembuatan mesin dan peralatan yang presisi.
• Penentuan lintasan dan sudut proyektil.

Bidang Lainnya

Kedudukan garis juga memiliki aplikasi dalam bidang lain, seperti:

• Seni dan Desain: Untuk menciptakan perspektif dan komposisi yang estetis.
• Survei dan Pemetaan: Untuk menentukan batas tanah dan fitur geografis.
• Medis: Untuk menganalisis gambar X-ray dan hasil diagnostik lainnya.

Ringkasan Terakhir

Kesimpulannya, kedudukan garis pada bidang adalah konsep dasar dalam geometri yang memberikan pemahaman penting tentang hubungan spasial antar garis. Mengetahui cara menentukan dan mengaplikasikan kedudukan garis sangat penting untuk menyelesaikan masalah geometrik, serta memiliki implikasi praktis dalam berbagai bidang.

Pertanyaan yang Sering Diajukan

Apa itu kedudukan garis pada bidang?

Kedudukan garis pada bidang menggambarkan hubungan posisi dua atau lebih garis dalam bidang datar.

Apa saja jenis-jenis kedudukan garis?

Jenis-jenis kedudukan garis meliputi: sejajar, tegak lurus, berpotongan, dan sejajar semu.

Bagaimana cara menentukan kedudukan garis?

Kedudukan garis dapat ditentukan dengan membandingkan kemiringan atau gradien garis-garis tersebut.

Apa saja aplikasi kedudukan garis dalam geometri?

Kedudukan garis digunakan untuk menentukan sifat bangun, seperti jenis segitiga, bentuk segi empat, dan posisi lingkaran.

Apa saja aplikasi kedudukan garis dalam kehidupan nyata?

Kedudukan garis diaplikasikan dalam arsitektur (desain bangunan), teknik (jembatan dan jalan), serta bidang lainnya yang melibatkan pengukuran dan konstruksi.