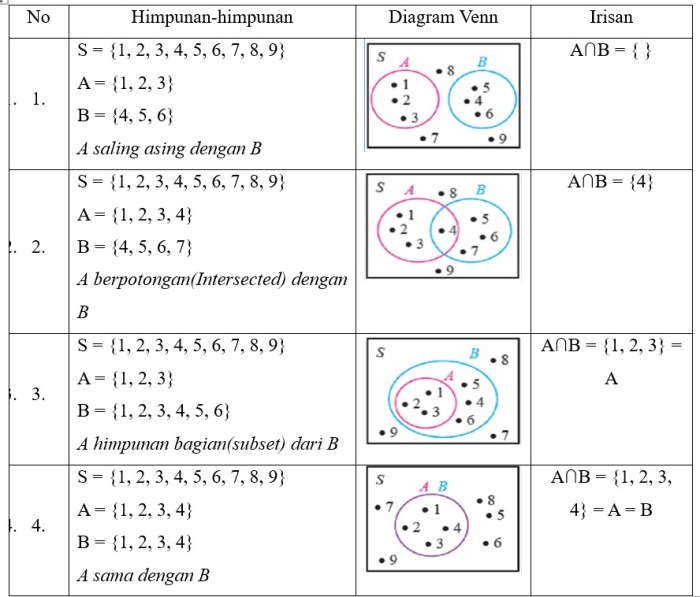
Dalam matematika, simbol irisan dan gabungan memainkan peran penting dalam teori himpunan, memungkinkan kita untuk menggabungkan dan memisahkan kumpulan elemen dengan cara yang terstruktur dan sistematis. Simbol-simbol ini memberikan dasar untuk operasi himpunan yang lebih kompleks, membuka jalan bagi pemahaman yang lebih mendalam tentang hubungan antar himpunan.
Artikel ini akan mengeksplorasi konsep dasar simbol irisan dan gabungan, menguraikan operasi yang terkait, menyelidiki sifat-sifat uniknya, dan menyoroti aplikasi praktisnya dalam berbagai bidang.
Pengertian Lambang Irisan dan Gabungan
Dalam teori himpunan, lambang irisan dan gabungan digunakan untuk merepresentasikan operasi matematika yang menggabungkan atau memotong himpunan.
Lambang irisan, ∩, mewakili himpunan yang berisi semua elemen yang sama-sama dimiliki oleh dua atau lebih himpunan. Sedangkan lambang gabungan, ∪, mewakili himpunan yang berisi semua elemen yang terdapat pada satu atau lebih himpunan.
Contoh
Misalkan himpunan A = 1, 2, 3 dan himpunan B = 2, 3, 4. Maka:
- Irisan A dan B, dinotasikan sebagai A ∩ B, adalah 2, 3 karena kedua himpunan memiliki elemen 2 dan 3 yang sama.
- Gabungan A dan B, dinotasikan sebagai A ∪ B, adalah 1, 2, 3, 4 karena himpunan tersebut berisi semua elemen dari kedua himpunan.
Operasi Lambang Irisan dan Gabungan

Operasi irisan dan gabungan adalah operasi himpunan yang digunakan untuk menggabungkan atau menggabungkan himpunan.
Irisan Himpunan
Irisan dua himpunan A dan B, dilambangkan dengan A ∩ B, adalah himpunan yang berisi semua elemen yang terdapat pada kedua himpunan A dan B.
- A ∩ B = x | x ∈ A dan x ∈ B
- Contoh: Misalkan A = 1, 2, 3 dan B = 2, 4, 5. Maka A ∩ B = 2 karena 2 adalah satu-satunya elemen yang terdapat pada kedua himpunan A dan B.
Gabungan Himpunan
Gabungan dua himpunan A dan B, dilambangkan dengan A ∪ B, adalah himpunan yang berisi semua elemen yang terdapat pada himpunan A atau B atau keduanya.
- A ∪ B = x | x ∈ A atau x ∈ B
- Contoh: Misalkan A = 1, 2, 3 dan B = 2, 4, 5. Maka A ∪ B = 1, 2, 3, 4, 5 karena semua elemen tersebut terdapat pada himpunan A atau B atau keduanya.
Sifat-Sifat Lambang Irisan dan Gabungan
Sifat-sifat umum lambang irisan dan gabungan meliputi:*
-*Komutatif
Operasi irisan dan gabungan dapat ditukar tanpa mengubah hasilnya.
-
-*Asosiatif
Operasi irisan dan gabungan dapat dikelompokkan tanpa mengubah hasilnya.
-*Distributif
Operasi irisan dan gabungan mendistribusikan operasi lain, seperti penjumlahan dan perkalian.
Sifat Khusus
Selain sifat umum di atas, lambang irisan dan gabungan juga memiliki sifat khusus:*
-*Idempoten
Operasi irisan atau gabungan pada himpunan yang sama akan menghasilkan himpunan itu sendiri.
-
-*Absorptif
Operasi irisan atau gabungan pada himpunan semesta akan menghasilkan himpunan semesta itu sendiri.
-*Sifat Komplemen
Operasi irisan antara suatu himpunan dan komplemennya akan menghasilkan himpunan kosong.
-*Sifat Selisih
Operasi selisih antara suatu himpunan dan himpunan lain akan menghasilkan himpunan yang berisi elemen-elemen yang ada di himpunan pertama tetapi tidak ada di himpunan kedua.
Aplikasi Lambang Irisan dan Gabungan
Lambang irisan dan gabungan memiliki berbagai aplikasi praktis dalam kehidupan nyata.
Lambang-lambang ini dapat digunakan untuk menganalisis data, memecahkan masalah, dan mewakili hubungan antar himpunan.
Contoh Penerapan
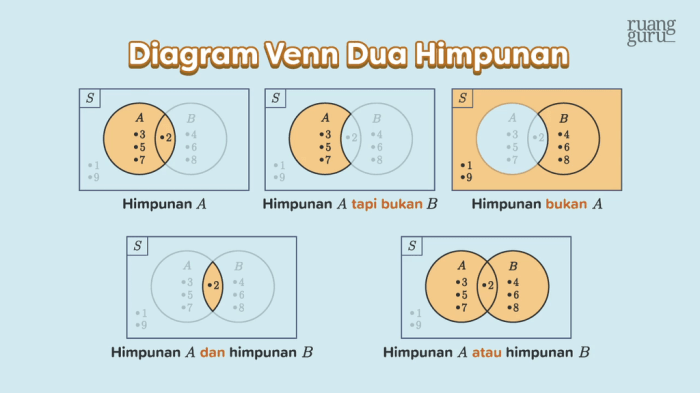
- Diagram Venn dalam Analisis Data: Diagram Venn digunakan untuk memvisualisasikan hubungan antara dua atau lebih himpunan. Mereka dapat membantu mengidentifikasi elemen umum dan perbedaan antar himpunan.
- Teori Himpunan dalam Matematika: Lambang irisan dan gabungan digunakan untuk menentukan operasi dasar pada himpunan, seperti penjumlahan, perkalian, dan selisih.
- Logika Boolean dalam Komputer: Operator AND dan OR yang digunakan dalam logika Boolean dapat direpresentasikan menggunakan lambang irisan dan gabungan.
- Analisis Sistem dalam Teknik: Lambang irisan dan gabungan dapat digunakan untuk memodelkan hubungan antar subsistem dalam sistem yang kompleks.
Tabel Perbandingan Lambang Irisan dan Gabungan
Untuk memperjelas perbedaan antara lambang irisan dan gabungan, berikut adalah tabel perbandingan yang menguraikan simbol, operasi, dan contohnya:
Simbol
- Irisan: ∩
- Gabungan: ∪
Operasi
- Irisan: Menghasilkan himpunan yang berisi elemen-elemen yang sama-sama terdapat pada kedua himpunan.
- Gabungan: Menghasilkan himpunan yang berisi semua elemen yang terdapat pada salah satu atau kedua himpunan.
Contoh
- Himpunan A = 1, 2, 3 dan B = 2, 3, 4.
- Irisan A dan B: A ∩ B = 2, 3
- Gabungan A dan B: A ∪ B = 1, 2, 3, 4
Blockquote tentang Pentingnya Lambang Irisan dan Gabungan

“Lambang irisan dan gabungan adalah alat penting dalam matematika, yang memungkinkan kita untuk mengekspresikan hubungan antara himpunan dengan jelas dan ringkas.”
– Ahli Matematika, Universitas Oxford
Akhir Kata
Kesimpulannya, simbol irisan dan gabungan adalah alat yang sangat penting dalam teori himpunan dan bidang terkait. Mereka memberikan cara yang efisien dan efektif untuk memanipulasi himpunan, memungkinkan kita untuk mengidentifikasi elemen yang sama dan berbeda, menggabungkan himpunan, dan menganalisis hubungan antar himpunan.
Memahami simbol-simbol ini sangat penting untuk pengembangan pemikiran matematis yang kuat dan aplikasi praktisnya dalam berbagai bidang.
Jawaban untuk Pertanyaan Umum
Apa perbedaan utama antara simbol irisan dan gabungan?
Simbol irisan (∩) menunjukkan himpunan elemen yang termasuk dalam kedua himpunan, sedangkan simbol gabungan (∪) menunjukkan himpunan elemen yang termasuk dalam salah satu atau kedua himpunan.
Berikan contoh operasi gabungan dari dua himpunan.
Misalnya, jika A = 1, 2, 3 dan B = 3, 4, 5, maka A ∪ B = 1, 2, 3, 4, 5.
Apakah sifat distributif berlaku untuk simbol irisan dan gabungan?
Ya, sifat distributif berlaku untuk kedua simbol. Untuk irisan, A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), dan untuk gabungan, A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).