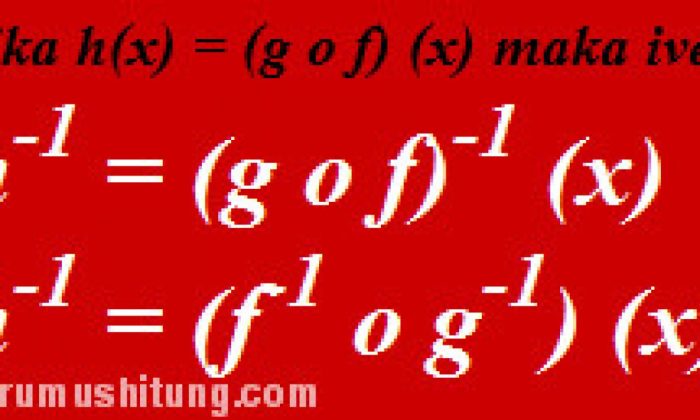Dalam matematika, komposisi invers merupakan konsep penting yang melibatkan penggabungan fungsi. Ketika dua fungsi dikomposisikan, urutan penerapannya menjadi krusial, karena dapat menghasilkan fungsi yang sama sekali berbeda.

Konsep komposisi invers mengeksplorasi hubungan antara fungsi dan inversnya, memberikan pemahaman mendalam tentang sifat dan perilaku fungsi.

Pengertian Komposisi Invers

Komposisi invers adalah operasi matematika yang melibatkan dua fungsi, di mana hasil dari satu fungsi diumpankan sebagai masukan ke fungsi lainnya, dan kemudian hasilnya diumpankan kembali sebagai masukan ke fungsi pertama.

Secara formal, jika kita memiliki dua fungsi f(x) dan g(x), maka komposisi inversnya ditulis sebagai f∘g(x) = f(g(x)).

Contoh Komposisi Invers

• Misalkan f(x) = x^2 dan g(x) = x +
  1. Maka komposisi inversnya adalah:
• f∘g(x) = f(g(x)) = f(x + 1) = (x + 1)^2
• g∘f(x) = g(f(x)) = g(x^2) = x^2 + 1

Jenis-jenis Komposisi Invers

Komposisi invers merupakan fungsi yang membatalkan fungsi lain. Berikut adalah jenis-jenis komposisi invers:

Fungsi Invers

Fungsi invers dari fungsi f(x) adalah fungsi f ^-1 (x) yang memenuhi f(f ^-1 (x)) = f ^-1 (f(x)) = x .

Fungsi Refleksi

Fungsi refleksi adalah fungsi yang memetakan titik ( x , y ) ke titik ( -x , y ) atau ( x , -y ). Fungsi refleksi terhadap sumbu x adalah f(x) = -x , sedangkan fungsi refleksi terhadap sumbu y adalah f(x) = y .

Fungsi Translasi

Fungsi translasi adalah fungsi yang menggeser grafik fungsi ke kiri, kanan, atas, atau bawah. Fungsi translasi ke kiri sebesar a adalah f(x) = f(x + a) , sedangkan fungsi translasi ke atas sebesar b adalah f(x) = f(x) + b .

Fungsi Rotasi

Fungsi rotasi adalah fungsi yang memutar grafik fungsi sebesar 90°, 180°, atau 270° berlawanan arah jarum jam. Fungsi rotasi sebesar 90° berlawanan arah jarum jam adalah f(x) = f(y) , sedangkan fungsi rotasi sebesar 180° berlawanan arah jarum jam adalah f(x) = f(-x, -y) .

Fungsi Skala

Fungsi skala adalah fungsi yang mengubah ukuran grafik fungsi. Fungsi skala dengan faktor k adalah f(x) = kf(x) .

Cara Menyelesaikan Komposisi Invers

Komposisi invers adalah operasi matematika yang membalikkan urutan operasi dalam suatu fungsi komposisi. Untuk menyelesaikan komposisi invers, ikuti langkah-langkah berikut:

Langkah-langkah Menyelesaikan Komposisi Invers

1. Tentukan fungsi komposisi yang akan dibalik.
2. Tulis fungsi invers dari setiap fungsi yang terlibat dalam komposisi.
3. Ganti setiap fungsi dalam komposisi dengan inversnya.
4. Sederhanakan hasilnya untuk mendapatkan komposisi invers.

Contoh

Misalkan kita memiliki komposisi fungsi berikut:f(x) = x^2 + 1g(x) = sqrt(x)Untuk mencari komposisi inversnya, kita perlu membalikkan urutan operasinya.f^(-1)(x) = sqrt(x

1)

g^(-1)(x) = x^2Komposisi inversnya menjadi:(f o g)^(-1)(x) = f^(-1)(g(x)) = f^(-1)(sqrt(x)) = sqrt(sqrt(x)

1)

Contoh Soal dan Pembahasan

Komposisi invers adalah operasi matematika yang melibatkan komposisi dua fungsi dan kemudian membalik urutan penerapannya. Berikut adalah beberapa contoh soal komposisi invers beserta pembahasannya:

Soal 1

Misalkan fungsi f(x) = x^2 dan g(x) = x + 1. Tentukan (f ∘ g)(x) dan (g ∘ f)(x).

Pembahasan:

• (f ∘ g)(x) = f(g(x)) = f(x + 1) = (x + 1)^2
• (g ∘ f)(x) = g(f(x)) = g(x^2) = x^2 + 1

Soal 2

Misalkan fungsi h(x) = |x| dan k(x) = 2x – 3. Tentukan (h ∘ k)(x) dan (k ∘ h)(x).

Pembahasan:

• (h ∘ k)(x) = h(k(x)) = h(2x
  – 3) = |2x
  – 3|
• (k ∘ h)(x) = k(h(x)) = k(|x|) = 2|x|
  – 3

Soal 3

Misalkan fungsi m(x) = e^x dan n(x) = ln(x). Tentukan (m ∘ n)(x) dan (n ∘ m)(x).

Pembahasan:

• (m ∘ n)(x) = m(n(x)) = m(ln(x)) = e^(ln(x)) = x
• (n ∘ m)(x) = n(m(x)) = n(e^x) = ln(e^x) = x

Dari ketiga contoh di atas, dapat dilihat bahwa komposisi invers tidak selalu menghasilkan fungsi yang sama. Dalam Soal 1 dan 2, komposisi invers menghasilkan fungsi yang berbeda, sedangkan pada Soal 3, komposisi invers menghasilkan fungsi identitas (y = x).

5 Tips Menyelesaikan Komposisi Invers

Komposisi invers adalah proses membalikkan urutan operasi dalam suatu fungsi komposisi. Ini bisa menjadi tugas yang menantang, tetapi ada beberapa tips yang dapat membantu Anda menyelesaikannya secara efektif.

Berikut adalah lima tips untuk menyelesaikan komposisi invers:

Langkah-Langkah Menentukan Komposisi Invers

1. Tentukan fungsi dalam dan luar komposisi.
2. Ganti argumen fungsi dalam dengan invers fungsi luar.
3. Sederhanakan hasilnya.

Contoh

Misalkan kita memiliki komposisi fungsi f(g(x)). Untuk menemukan inversnya, kita perlu mengikuti langkah-langkah berikut:

• Fungsi dalam: g(x)
• Fungsi luar: f(x)
• Invers fungsi luar: f^-1(x)
• Invers komposisi: f^-1(g(x))

Ringkasan Terakhir

Dengan memahami konsep komposisi invers dan menguasai teknik penyelesaiannya, siswa dapat mengembangkan keterampilan analitis yang kuat dan memperoleh pemahaman yang lebih baik tentang fungsi dan transformasi.

Pertanyaan yang Sering Diajukan

Apa saja jenis-jenis komposisi invers?

Ada tiga jenis utama komposisi invers: komposisi invers kiri, komposisi invers kanan, dan komposisi invers dua sisi.

Bagaimana cara menyelesaikan komposisi invers kiri?

Untuk menyelesaikan komposisi invers kiri, terapkan fungsi invers pada sisi kiri persamaan.

Apa pentingnya komposisi invers dalam matematika?

Komposisi invers membantu menentukan apakah suatu fungsi memiliki invers, memahami sifat fungsi komposit, dan memecahkan berbagai persamaan.