Segitiga, salah satu bangun datar yang paling fundamental dalam geometri, memiliki sifat dan karakteristik yang telah dipelajari selama berabad-abad. Diketahui segitiga PQR, sebuah bangun tiga sisi yang membentuk sudut dalam dan luar yang unik, kita akan menyelidiki berbagai aspeknya, termasuk sudut, sisi, luas, keliling, jenis, garis berat, garis tinggi, dan sifat-sifat khusus.
Dengan pemahaman yang komprehensif tentang segitiga PQR, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat geometris dan menerapkan pengetahuan ini dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.
Sudut Segitiga PQR
Dalam geometri, sudut segitiga adalah ukuran bukaan antara dua sisi segitiga. Sudut segitiga diukur dalam derajat, dengan satu derajat sama dengan 1/360 dari satu putaran penuh.
Jenis Sudut dalam Segitiga PQR
- Sudut lancip: Sudut yang besarnya kurang dari 90 derajat.
- Sudut siku-siku: Sudut yang besarnya tepat 90 derajat.
- Sudut tumpul: Sudut yang besarnya lebih dari 90 derajat dan kurang dari 180 derajat.
Hubungan Sudut dalam Segitiga PQR
Jumlah ketiga sudut dalam segitiga PQR selalu sama dengan 180 derajat. Hubungan ini dikenal sebagai Teorema Jumlah Sudut Segitiga.
Tabel Sudut Segitiga PQR
| Sudut | Besar | Jenis |
|---|---|---|
| ∠PQR | x | Lancip, siku-siku, atau tumpul |
| ∠PQS | y | Lancip, siku-siku, atau tumpul |
| ∠QRS | z | Lancip, siku-siku, atau tumpul |
| Jumlah Sudut | x + y + z = 180° | – |
Sisi Segitiga PQR
Segitiga adalah poligon tiga sisi dengan tiga sisi dan tiga sudut. Sisi-sisi segitiga membentuk kerangka bangun tersebut dan menentukan sifat-sifat geometrisnya.
Sifat-sifat Sisi Segitiga
Sisi-sisi segitiga memiliki beberapa sifat penting, antara lain:
- Panjang: Panjang sisi adalah jarak antara dua titik ujungnya.
- Relasi Panjang: Dalam segitiga, jumlah panjang dua sisi mana pun selalu lebih besar dari panjang sisi ketiga (pertidaksamaan segitiga).
- Kesamaan: Dua sisi segitiga dikatakan sama jika memiliki panjang yang sama.
- Ketidaksetaraan: Dua sisi segitiga dikatakan tidak sama jika memiliki panjang yang berbeda.
Contoh Sisi dalam Segitiga PQR
Segitiga PQR dapat memiliki berbagai kemungkinan panjang sisi, termasuk:
- Semua sisi sama panjang (segitiga sama sisi)
- Dua sisi sama panjang (segitiga sama kaki)
- Tidak ada sisi yang sama panjang (segitiga sembarang)
Hubungan Panjang Sisi
Panjang sisi-sisi dalam segitiga PQR saling terkait melalui beberapa hubungan, yaitu:
- Teorema Pythagoras: Untuk segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi lainnya.
- Pertidaksamaan Segitiga: Jumlah panjang dua sisi mana pun selalu lebih besar dari panjang sisi ketiga.
- Ketidaksetaraan Segitiga: Selisih panjang dua sisi mana pun selalu lebih kecil dari panjang sisi ketiga.
Luas Segitiga PQR
Luas segitiga merupakan ukuran bidang permukaan segitiga yang dibentuk oleh tiga sisi yang saling terhubung pada tiga titik sudut. Luas segitiga dapat dihitung menggunakan rumus tertentu.
Rumus Luas Segitiga
Rumus luas segitiga adalah sebagai berikut:
Luas = 1/2 x alas x tinggi
Dimana:
- Luas adalah luas segitiga yang akan dihitung
- Alas adalah panjang salah satu sisi segitiga
- Tinggi adalah jarak tegak lurus dari alas ke titik sudut yang berlawanan
Contoh Perhitungan Luas Segitiga PQR
Misalkan segitiga PQR memiliki alas 10 cm dan tinggi 8 cm. Luas segitiga PQR dapat dihitung sebagai berikut:
Luas = 1/2 x 10 cm x 8 cm = 40 cm 2
Faktor-faktor yang Mempengaruhi Luas Segitiga PQR
Luas segitiga PQR dapat dipengaruhi oleh beberapa faktor, antara lain:
- Panjang alas: Semakin panjang alas segitiga, semakin besar luasnya.
- Tinggi segitiga: Semakin tinggi segitiga, semakin besar luasnya.
- Sudut antara alas dan tinggi: Sudut yang lebih besar antara alas dan tinggi akan menghasilkan luas yang lebih besar.
Keliling Segitiga PQR
Keliling segitiga adalah jumlah panjang semua sisinya. Rumus untuk menghitung keliling segitiga adalah:
K = a + b + c
di mana:
- K adalah keliling segitiga
- a, b, dan c adalah panjang sisi-sisi segitiga
Contoh Perhitungan Keliling Segitiga PQR
Misalkan segitiga PQR memiliki sisi a = 5 cm, b = 7 cm, dan c = 9 cm. Keliling segitiga PQR adalah:
K = a + b + cK = 5 cm + 7 cm + 9 cmK = 21 cm
Perbandingan Keliling Segitiga PQR dengan Segitiga Lainnya
Tabel berikut membandingkan keliling segitiga PQR dengan keliling segitiga lainnya:
| Segitiga | Panjang Sisi (cm) | Keliling (cm) |
|---|---|---|
| PQR | 5, 7, 9 | 21 |
| XYZ | 4, 6, 8 | 18 |
| ABC | 3, 5, 7 | 15 |
Jenis Segitiga PQR
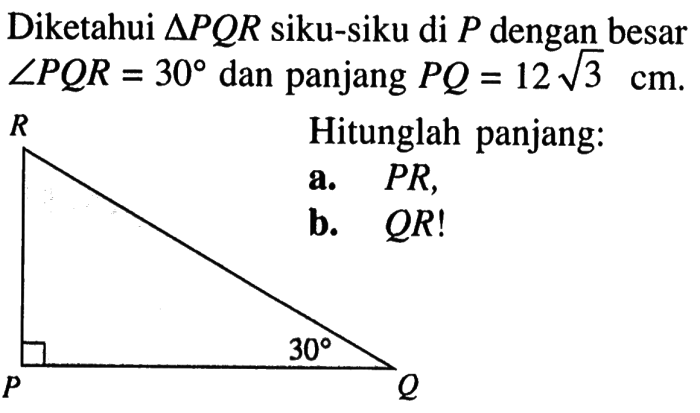
Segitiga PQR dapat diklasifikasikan ke dalam beberapa jenis berdasarkan ukuran sudut-sudutnya.
Jenis Segitiga Berdasarkan Sudut
- Segitiga Lancip: Ketiga sudutnya kurang dari 90 derajat.
- Segitiga Siku-siku: Salah satu sudutnya berukuran tepat 90 derajat.
- Segitiga Tumpul: Salah satu sudutnya lebih besar dari 90 derajat.
Setiap segitiga PQR dapat diklasifikasikan ke dalam salah satu dari jenis ini berdasarkan pengukuran sudut-sudutnya.
Garis Berat dan Garis Tinggi Segitiga PQR

Dalam geometri, garis berat dan garis tinggi segitiga merupakan garis yang memiliki sifat khusus dan memainkan peran penting dalam menentukan luas dan sifat-sifat segitiga.
Konsep Garis Berat
Garis berat segitiga adalah ruas garis yang menghubungkan titik sudut segitiga dengan titik tengah sisi yang berhadapan. Garis berat membagi segitiga menjadi dua bagian yang luasnya sama.
Dalam segitiga PQR, garis berat yang menghubungkan titik sudut P dengan titik tengah sisi QR dilambangkan dengan h a . Demikian pula, garis berat yang menghubungkan titik sudut Q dan R dengan titik tengah sisi yang berhadapan dilambangkan dengan h b dan h c .
Konsep Garis Tinggi
Garis tinggi segitiga adalah ruas garis yang ditarik tegak lurus dari titik sudut segitiga ke sisi yang berhadapan atau perpanjangannya. Garis tinggi membagi segitiga menjadi dua bagian yang luasnya sama.
Dalam segitiga PQR, garis tinggi yang ditarik dari titik sudut P ke sisi QR dilambangkan dengan h a ‘. Demikian pula, garis tinggi yang ditarik dari titik sudut Q dan R dengan sisi yang berhadapan dilambangkan dengan h b ‘ dan h c ‘.
Ilustrasi Garis Berat dan Garis Tinggi
Gambar berikut menunjukkan garis berat dan garis tinggi segitiga PQR:
[Masukkan ilustrasi garis berat dan garis tinggi segitiga PQR di sini]
Cara Menentukan Panjang Garis Berat dan Garis Tinggi
Panjang garis berat dan garis tinggi segitiga dapat ditentukan menggunakan rumus-rumus berikut:
- Panjang garis berat: h = (2/3) x sisi yang berhadapan
- Panjang garis tinggi: h’ = (1/2) x sisi yang berhadapan
Sebagai contoh, jika sisi QR dari segitiga PQR memiliki panjang 6 cm, maka panjang garis berat h a adalah (2/3) x 6 cm = 4 cm. Dan panjang garis tinggi h a ‘ adalah (1/2) x 6 cm = 3 cm.
Sifat-Sifat Khusus Segitiga PQR

Segitiga PQR memiliki beberapa sifat khusus yang dapat dikategorikan menjadi segitiga sama sisi, segitiga sama kaki, dan segitiga siku-siku. Sifat-sifat ini ditentukan oleh panjang sisi dan sudut-sudutnya.
Segitiga Sama Sisi
Segitiga sama sisi adalah segitiga yang memiliki tiga sisi yang sama panjang. Pada segitiga PQR, jika panjang ketiga sisinya adalah sama, maka segitiga PQR adalah segitiga sama sisi. Misalnya, jika panjang sisi PQ, QR, dan PR adalah 5 cm, maka segitiga PQR adalah segitiga sama sisi.
Segitiga Sama Kaki
Segitiga sama kaki adalah segitiga yang memiliki dua sisi yang sama panjang. Pada segitiga PQR, jika panjang dua sisi, misalnya PQ dan PR, adalah sama, maka segitiga PQR adalah segitiga sama kaki. Misalnya, jika panjang sisi PQ dan PR adalah 6 cm dan panjang sisi QR adalah 8 cm, maka segitiga PQR adalah segitiga sama kaki.
Segitiga Siku-Siku
Segitiga siku-siku adalah segitiga yang memiliki satu sudut siku-siku (90 derajat). Pada segitiga PQR, jika salah satu sudut, misalnya sudut Q, adalah 90 derajat, maka segitiga PQR adalah segitiga siku-siku. Misalnya, jika sudut Q adalah 90 derajat, maka segitiga PQR adalah segitiga siku-siku.
Ringkasan Akhir

Melalui analisis menyeluruh tentang segitiga PQR, kita telah memperoleh pemahaman yang komprehensif tentang sudut, sisi, luas, keliling, jenis, garis berat, garis tinggi, dan sifat-sifat khusus yang terkait dengannya. Pengetahuan ini tidak hanya memperkaya apresiasi kita terhadap geometri tetapi juga membekali kita dengan alat penting untuk memecahkan masalah dan memahami konsep yang lebih kompleks dalam matematika dan bidang terkait.
Pertanyaan Umum (FAQ)
Apa itu garis berat segitiga?
Garis berat segitiga adalah ruas garis yang ditarik dari titik sudut segitiga ke titik tengah sisi yang berlawanan.
Bagaimana cara menentukan luas segitiga jika diketahui dua sisinya?
Luas segitiga dapat ditentukan dengan menggunakan rumus: Luas = (1/2) x alas x tinggi, di mana alas adalah salah satu sisi yang diketahui dan tinggi adalah garis tinggi yang ditarik dari titik sudut yang berlawanan dengan alas tersebut.
Apa saja jenis-jenis segitiga berdasarkan sudutnya?
Berdasarkan sudutnya, segitiga dapat diklasifikasikan menjadi tiga jenis: segitiga siku-siku (memiliki satu sudut siku-siku), segitiga lancip (memiliki tiga sudut lancip), dan segitiga tumpul (memiliki satu sudut tumpul).
