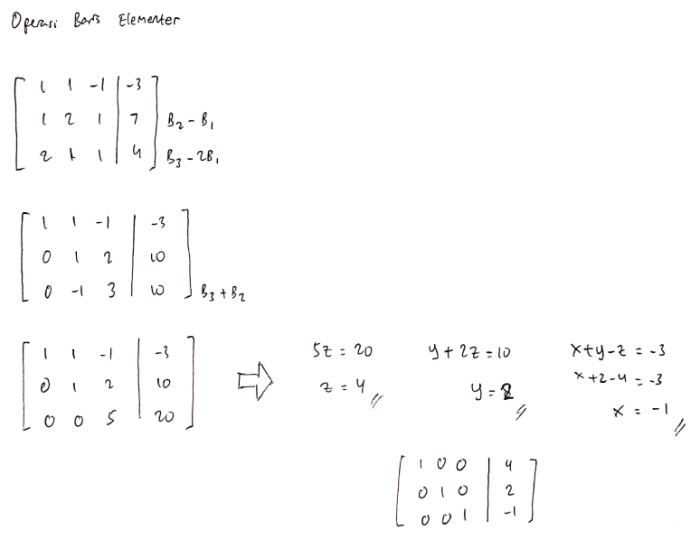Eliminasi Gauss, teknik yang ampuh untuk menyelesaikan sistem persamaan linear, telah banyak digunakan selama berabad-abad. Dalam artikel ini, kita akan menjelajahi contoh soal eliminasi Gauss 3×3, memahami cara kerjanya, dan mengungkap manfaatnya yang luar biasa.
Dengan mengikuti langkah-langkah sederhana dan contoh yang mudah dipahami, kita akan memberdayakan pembaca untuk menaklukkan sistem persamaan yang menantang dengan percaya diri.
Contoh Soal Eliminasi Gauss 3×3

Eliminasi Gauss adalah metode untuk menyelesaikan sistem persamaan linear dengan menggunakan operasi baris elementer. Berikut adalah beberapa contoh soal eliminasi Gauss 3×3:
Contoh Soal dan Penyelesaian
| Contoh Soal | Penyelesaian |
|---|---|
|
x + y – z = 0 2x + 3y + z = 1 x – y + 2z = 5 |
x = 2 y = 1 z = 1 |
|
2x + y – z = 1 x + 2y + 3z = 6 x – y + z = 2 |
x = 1 y = 2 z = 1 |
|
x + y + z = 6 2x + 3y + 4z = 14 x – y + 2z = 5 |
x = 2 y = 1 z = 3 |
Cara Eliminasi Gauss 3×3
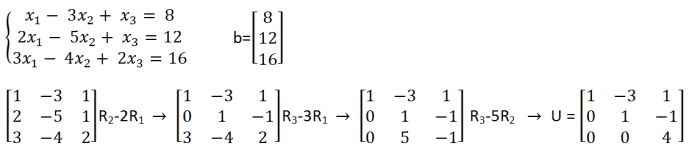
Eliminasi Gauss adalah metode sistematis untuk menyelesaikan sistem persamaan linier dengan menggunakan operasi baris elementer. Untuk sistem persamaan 3×3, eliminasi Gauss melibatkan langkah-langkah berikut:
Langkah-Langkah Eliminasi Gauss 3×3
- Ubah matriks koefisien menjadi bentuk eselon baris.
- Gunakan operasi baris elementer untuk mendapatkan matriks identitas pada bagian kiri matriks eselon baris.
- Selesaikan sistem persamaan yang dihasilkan dengan menggunakan matriks identitas.
Prosedur Eliminasi Gauss 3×3
Eliminasi Gauss adalah metode untuk menyelesaikan sistem persamaan linear dengan mengurangi matriks koefisien menjadi bentuk eselon baris tereduksi (RREF).
Berikut adalah prosedur eliminasi Gauss untuk matriks 3×3:
Membuat Matriks Gabungan
Gabungkan matriks koefisien dengan matriks konstanta, membentuk matriks gabungan.
Mengubah Baris Pertama menjadi Bentuk Eselon Baris
Ubah baris pertama menjadi bentuk eselon baris, dengan elemen diagonal (kiri atas) menjadi 1 dan elemen lainnya di kolom yang sama menjadi 0.
Mengeliminasi Elemen di Bawah Diagonal Kiri Atas
Gunakan baris pertama untuk mengeliminasi elemen di bawah diagonal kiri atas dengan mengalikan baris pertama dengan faktor yang sesuai dan menambahkannya ke baris yang akan dieliminasi.
Mengubah Baris Kedua menjadi Bentuk Eselon Baris
Ulangi langkah 2 untuk baris kedua, dengan mengabaikan kolom yang sudah dieliminasi pada langkah sebelumnya.
Mengeliminasi Elemen di Bawah Diagonal Kiri Tengah
Gunakan baris kedua untuk mengeliminasi elemen di bawah diagonal kiri tengah dengan cara yang sama seperti langkah 3.
Menyelesaikan Sistem
Setelah matriks berada dalam bentuk RREF, selesaikan sistem persamaan dengan membaca nilai variabel dari baris terakhir ke baris pertama.
Contoh Penerapan Eliminasi Gauss 3×3
Eliminasi Gauss adalah metode sistematis untuk menyelesaikan sistem persamaan linear dengan mengubah matriks koefisien menjadi matriks eselon baris tereduksi.
Contoh Penyelesaian Sistem Persamaan 3×3
Misalkan kita memiliki sistem persamaan 3×3 berikut:
2x + 3y
|
x
|
3x + 2y
|
Kita dapat menyelesaikan sistem ini menggunakan eliminasi Gauss:
- Eliminasi pada Baris 1: Kalikan baris 1 dengan 1/2 untuk mendapatkan koefisien 1 pada x pada baris 1.
- Eliminasi pada Baris 2: Kurangi baris 2 dengan baris 1 dikalikan dengan 1/2 untuk menghilangkan koefisien x pada baris 2.
- Eliminasi pada Baris 3: Kurangi baris 3 dengan baris 1 dikalikan dengan 3/2 untuk menghilangkan koefisien x pada baris 3.
- Eliminasi pada Baris 2: Kalikan baris 2 dengan
1 untuk mendapatkan koefisien 1 pada y pada baris 2.
- Eliminasi pada Baris 3: Kurangi baris 3 dengan baris 2 dikalikan dengan 2 untuk menghilangkan koefisien y pada baris 3.
- Eliminasi pada Baris 3: Kalikan baris 3 dengan
1/2 untuk mendapatkan koefisien 1 pada z pada baris 3.
- Substitusi Balik: Substitusikan nilai z dari baris 3 ke dalam baris 2 dan 1 untuk mendapatkan nilai y dan x.
Setelah eliminasi, kita mendapatkan matriks eselon baris tereduksi:
| 1 | 0 | 0 | 2 |
| 0 | 1 | 0 | 3 |
| 0 | 0 | 1 | -1 |
Dengan demikian, solusi sistem persamaan tersebut adalah:
- x = 2
- y = 3
- z =
-1
Manfaat Eliminasi Gauss 3×3
Eliminasi Gauss 3×3 adalah metode yang ampuh untuk menyelesaikan sistem persamaan linear dengan tiga variabel. Metode ini menawarkan beberapa manfaat yang menjadikannya teknik yang disukai untuk menyelesaikan sistem semacam itu.
Penyederhanaan Persamaan
- Menyederhanakan persamaan dengan menghilangkan variabel secara sistematis, menghasilkan persamaan yang lebih mudah untuk diselesaikan.
- Mengurangi jumlah variabel dalam sistem, membuatnya lebih mudah dikelola dan diselesaikan.
Akurasi yang Lebih Baik
- Meminimalkan kesalahan pembulatan dan akumulasi kesalahan karena persamaan diselesaikan secara bertahap.
- Menghasilkan solusi yang lebih akurat, terutama untuk sistem persamaan yang kompleks.
Aplikasi Luas
- Dapat digunakan untuk menyelesaikan berbagai masalah dunia nyata, seperti masalah teknik, fisika, dan ekonomi.
- Berlaku untuk sistem persamaan linear yang konsisten dan tidak konsisten, memberikan informasi yang berharga tentang solusi.
Efisiensi Komputasi
- Algoritme yang efisien yang dapat diimplementasikan dengan mudah dalam kalkulator atau perangkat lunak.
- Mengurangi waktu dan upaya yang diperlukan untuk menyelesaikan sistem persamaan linear yang besar.
Ilustrasi Eliminasi Gauss 3×3

Eliminasi Gauss adalah metode sistematis untuk menyelesaikan sistem persamaan linier dengan menggunakan operasi baris dasar. Berikut adalah ilustrasi proses eliminasi Gauss untuk sistem 3×3:
Langkah 1: Membuat Matriks Augmentasi
Tuliskan sistem persamaan linier dalam bentuk matriks augmentasi:
$$\beginbmatrix a_11 & a_12 & a_13 & b_1 \\\ a_21 & a_22 & a_23 & b_2 \\\ a_31 & a_32 & a_33 & b_3 \endbmatrix$$
Langkah 2: Menjadikan Elemen Pivot 1
Pilih baris dengan elemen pivot (elemen non-nol pertama di kolom) di kolom pertama. Jika tidak ada, tukar baris dengan baris di bawahnya yang memiliki elemen pivot.
Langkah 3: Mengnolkan Elemen Bawah Pivot
Gunakan operasi baris dasar untuk menolkan semua elemen di bawah elemen pivot di kolom pertama. Ini dilakukan dengan mengalikan baris pivot dengan faktor yang sesuai dan mengurangkannya dari baris di bawahnya.
Langkah 4: Mengulangi Langkah 2-3 untuk Kolom Selanjutnya
Ulangi langkah 2-3 untuk kolom berikutnya, memilih elemen pivot di kolom tersebut dan menolkan elemen di bawahnya.
Langkah 5: Memecahkan Sistem Persamaan
Matriks augmentasi sekarang dalam bentuk baris eselon tereduksi, yang dapat digunakan untuk menyelesaikan sistem persamaan dengan membaca solusi dari baris terakhir:
$$x_1 = \fracb_1a_11$$$$x_2 = \fracb_2a_22$$$$x_3 = \fracb_3a_33$$
Ringkasan Terakhir

Eliminasi Gauss 3×3 telah membuktikan dirinya sebagai metode yang andal dan efisien untuk menyelesaikan sistem persamaan linear. Kesederhanaan dan keefektifannya menjadikannya alat yang sangat berharga dalam berbagai disiplin ilmu, memberdayakan para peneliti, insinyur, dan siswa untuk mengatasi masalah matematika yang kompleks.
Pertanyaan Umum yang Sering Muncul
Apa itu eliminasi Gauss 3×3?
Eliminasi Gauss 3×3 adalah metode bertahap untuk menyelesaikan sistem persamaan linear yang melibatkan tiga variabel.
Mengapa mempelajari eliminasi Gauss 3×3 penting?
Eliminasi Gauss 3×3 memberikan dasar yang kuat untuk menyelesaikan sistem persamaan yang lebih kompleks dan memiliki aplikasi di berbagai bidang.
Bagaimana cara menerapkan eliminasi Gauss 3×3?
Ikuti langkah-langkah yang diuraikan dalam artikel: eliminasi baris, substitusi ke belakang, dan pemeriksaan solusi.