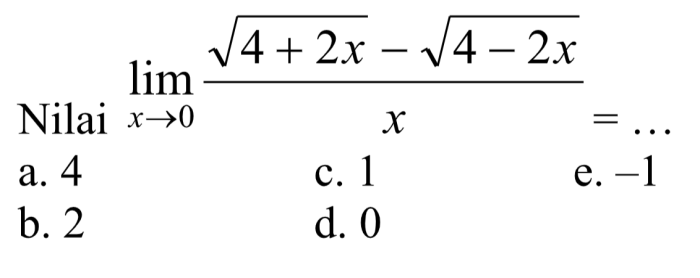Dalam matematika, limit memainkan peran penting dalam memahami perilaku fungsi saat variabel input mendekati nilai tertentu. Artikel ini akan fokus pada limit khusus, yaitu limit x mendekati 0. Dengan menjelajahi konsep ini secara mendalam, kita akan memperoleh pemahaman yang komprehensif tentang cara menentukan limit dan aplikasinya dalam berbagai bidang.
Konsep limit menyelidiki nilai yang didekati oleh fungsi saat variabel inputnya mendekati nilai tertentu. Dalam hal limit x mendekati 0, kita menyelidiki nilai yang didekati oleh fungsi saat x mendekati 0. Konsep ini sangat penting dalam kalkulus dan memiliki aplikasi yang luas dalam berbagai bidang matematika dan sains.
Pengertian Limit Fungsi

Limit fungsi adalah konsep dasar dalam kalkulus yang digunakan untuk menggambarkan perilaku fungsi saat argumennya mendekati nilai tertentu. Definisi formalnya adalah sebagai berikut:
Misalkan 𝑓(𝑥) adalah fungsi yang didefinisikan pada interval terbuka (𝑎, 𝑏) yang mengandung titik 𝑐. Maka limit 𝑓(𝑥) saat 𝑥 mendekati 𝑐, ditulis sebagai lim 𝑥→𝑐 𝑓(𝑥), adalah 𝐿 jika untuk setiap bilangan real 𝜀 > 0, terdapat bilangan real 𝛿 > 0 sehingga untuk semua 𝑥 memenuhi |𝑥 − 𝑐|< 𝛿, maka |𝑓(𝑥) − 𝐿| < 𝜀.
Fungsi dengan Limit
- 𝑓(𝑥) = 𝑥2, lim𝑥→0𝑓(𝑥) = 0
- 𝑓(𝑥) = sin(𝑥), lim𝑥→0𝑓(𝑥) = 0
Fungsi Tanpa Limit
- 𝑓(𝑥) = 1/𝑥, lim𝑥→0𝑓(𝑥) tidak ada (tak terdefinisi)
- 𝑓(𝑥) = |𝑥|, lim𝑥→0𝑓(𝑥) tidak ada (tak unik)
Cara Menentukan Limit
Menentukan limit fungsi merupakan proses mengevaluasi nilai suatu fungsi saat argumennya mendekati suatu nilai tertentu. Berikut adalah langkah-langkah untuk menentukan limit:
Substitusi Langsung
Jika fungsi terdefinisi pada nilai tertentu, limit dapat ditentukan dengan langsung mensubstitusikan nilai tersebut ke dalam fungsi. Misalnya, untuk mencari limit f(x) = x 2 saat x mendekati 0, kita dapat langsung mensubstitusikan x = 0 ke dalam fungsi:
lim x → 0 f(x) = lim x → 0 x 2 = 0 2 = 0
Pemfaktoran
Jika fungsi dapat difaktorkan, limit dapat ditentukan dengan menggunakan aturan limit berikut:
lim x → a [f(x)g(x)] = lim x → a f(x) – lim x → a g(x)
Misalnya, untuk mencari limit f(x) = (x – 1)(x + 2) saat x mendekati 1, kita dapat memfaktorkan fungsi dan menggunakan aturan limit:
lim x → 1 f(x) = lim x → 1 (x – 1)(x + 2) = lim x → 1 (x – 1) – lim x → 1 (x + 2) = 0 – 3 = 0
Pembagian Polinomial
Jika fungsi adalah rasional (yaitu, rasio dua polinomial), limit dapat ditentukan dengan menggunakan pembagian polinomial. Ini melibatkan membagi polinomial pembilang dengan polinomial penyebut. Limit fungsi sama dengan limit hasil bagi polinomial.
Misalnya, untuk mencari limit f(x) = (x 2 – 1)/(x – 1) saat x mendekati 1, kita dapat menggunakan pembagian polinomial:
x 2 – 1 / x – 1 = x + 1
Oleh karena itu, lim x → 1 f(x) = lim x → 1 (x + 1) = 1 + 1 = 2
Jenis-Jenis Limit
Dalam kalkulus, limit adalah konsep fundamental yang digunakan untuk mempelajari perilaku fungsi ketika input mendekati nilai tertentu. Terdapat beberapa jenis limit, antara lain:
Limit Satu Sisi
Limit satu sisi adalah limit ketika input mendekati suatu nilai dari satu arah, baik dari kiri atau dari kanan.
- Limit dari Kiri:
Misalkan fungsi f(x). Limit dari kiri di titik a ditulis sebagai:
$$lim_x \to a^- f(x)$$
di mana x mendekati a dari kiri (x < a). - Limit dari Kanan:
Limit dari kanan di titik a ditulis sebagai:
$$lim_x \to a^+ f(x)$$
di mana x mendekati a dari kanan (x > a).
Limit Tak Hingga
Limit tak hingga adalah limit ketika input mendekati tak hingga atau negatif tak hingga.
- Limit Tak Hingga:
Limit tak hingga dilambangkan dengan:
$$lim_x \to \infty f(x)$$
di mana x mendekati tak hingga. - Limit Negatif Tak Hingga:
Limit negatif tak hingga dilambangkan dengan:
$$lim_x \to
-\infty f(x)$$
di mana x mendekati negatif tak hingga.
Limit Tak Tentu
Limit tak tentu adalah limit yang tidak dapat ditentukan menggunakan metode langsung, seperti substitusi atau faktorisasi. Beberapa bentuk limit tak tentu antara lain:
- Bentuk 0/0:
Ketika limit dari pembilang dan penyebut sama dengan 0. - Bentuk ∞/∞:
Ketika limit dari pembilang dan penyebut sama dengan tak hingga. - Bentuk 1∞:
Ketika limit dari basis adalah 1 dan limit dari eksponen adalah tak hingga. - Bentuk ∞0:
Ketika limit dari basis adalah tak hingga dan limit dari eksponen adalah 0.
Aturan L’Hopital

Aturan L’Hopital adalah teknik matematika yang digunakan untuk mengevaluasi limit ketika bentuk tak tentu muncul.
Cara Menggunakan Aturan L’Hopital
- Tentukan bentuk tak tentu yang muncul pada limit.
- Ambil turunan pembilang dan penyebut secara terpisah.
- Evaluasi limit baru menggunakan hasil turunan.
Contoh Soal
Evaluasi limit berikut menggunakan aturan L’Hopital:
$$\lim_x \to 0 \frac\sin x
xx^3$$
Penyelesaian:
Bentuk tak tentu yang muncul adalah 0/0.
Mengambil turunan pembilang dan penyebut:
$$\lim_x \to 0 \frac\cos x
13x^2$$
Mengevaluasi limit baru:
$$\lim_x \to 0 \frac\cos 0
- 13(0)^2 = \frac-10 =
- \infty$$
Jadi, limit asli adalah $-\infty$.
Aplikasi Limit

Limit memiliki banyak aplikasi penting dalam matematika, termasuk:
- Mencari kemiringan garis singgung pada suatu kurva
- Mencari luas daerah di bawah kurva
Mencari Kemiringan Garis Singgung
Kemiringan garis singgung pada kurva di titik tertentu diberikan oleh turunan fungsi pada titik tersebut. Namun, turunan tidak selalu terdefinisi di setiap titik. Dalam kasus seperti itu, limit dapat digunakan untuk menemukan kemiringan garis singgung.Misalkan kita ingin mencari kemiringan garis singgung pada kurva y = x^2
di titik (0, 0)
. Turunan dari y = x^2
adalah y’ = 2x
, yang tidak terdefinisi di x = 0
. Namun, kita dapat menggunakan limit untuk menemukan kemiringan garis singgung sebagai berikut:$$\lim_x \to 0 \fracf(x)
- f(0)x
- 0 = \lim_x \to 0 \fracx^2
- 0x
- 0 = \lim_x \to 0 x = 0$$
Jadi, kemiringan garis singgung pada kurva y = x^2
di titik (0, 0)
adalah 0.
Mencari Luas Daerah
Luas daerah di bawah kurva dapat ditemukan dengan menggunakan integral. Namun, integral tidak selalu mudah untuk dievaluasi. Dalam kasus seperti itu, limit dapat digunakan untuk mencari luas daerah.Misalkan kita ingin mencari luas daerah di bawah kurva y = x^2
antara x = 0
dan x = 1
. Integral dari y = x^2
adalah \frac13x^3
, sehingga luas daerahnya adalah:$$\int_0^1 x^2 dx = \lim_n \to \infty \sum_i=1^n \left(\fracin\right)^2 \frac1n = \frac13$$Jadi, luas daerah di bawah kurva y = x^2
antara x = 0
dan x = 1
adalah \frac13
.
Akhir Kata

Limit x mendekati 0 merupakan konsep mendasar dalam matematika yang menyediakan alat yang ampuh untuk menganalisis perilaku fungsi. Dengan memahami konsep ini dan teknik untuk menentukan limit, kita dapat memecahkan masalah matematika yang kompleks dan memperoleh wawasan berharga tentang dunia di sekitar kita.
Bagian Pertanyaan Umum (FAQ)
Apa itu limit fungsi?
Limit fungsi adalah nilai yang didekati oleh fungsi saat variabel inputnya mendekati nilai tertentu.
Bagaimana cara menentukan limit x mendekati 0?
Ada beberapa metode untuk menentukan limit x mendekati 0, seperti substitusi langsung, pemfaktoran, dan pembagian polinomial.
Apa saja jenis-jenis limit?
Jenis-jenis limit meliputi limit satu sisi, limit tak hingga, dan limit tak tentu.
Apa itu aturan L’Hopital?
Aturan L’Hopital adalah teknik untuk menentukan limit tak tentu dengan menggunakan turunan.
Apa saja aplikasi limit?
Limit memiliki banyak aplikasi dalam matematika, seperti mencari kemiringan garis singgung dan mencari luas daerah.