Dalam dunia matematika, barisan geometri memegang peranan penting sebagai urutan bilangan yang membentuk pola perkalian yang konsisten. Salah satu contoh barisan geometri yang umum ditemui adalah 5, 15, dan 45, yang akan menjadi fokus utama pembahasan dalam uraian ini.

Konsep barisan geometri akan dijabarkan secara mendalam, mencakup rumus-rumus yang digunakan, sifat-sifat yang dimilikinya, serta penerapannya dalam menyelesaikan permasalahan dan dalam berbagai bidang kehidupan nyata.

Pengertian Barisan Geometri

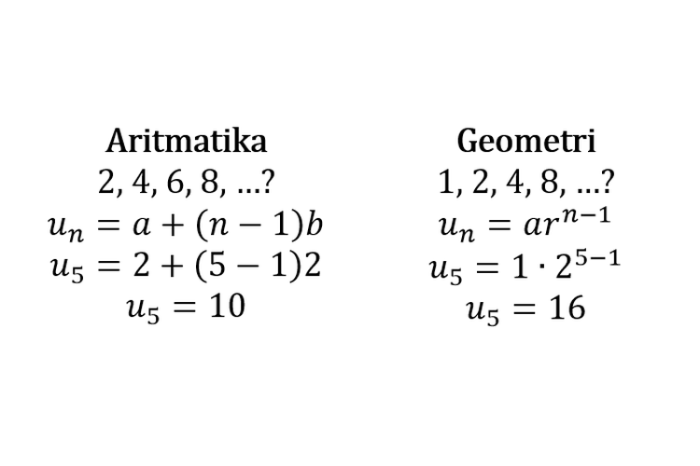
Barisan geometri adalah barisan bilangan yang setiap suku selanjutnya diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio.

Misalnya, barisan 5, 15, 45, 135, … adalah barisan geometri dengan rasio 3.

Rumus Barisan Geometri

Barisan geometri adalah barisan bilangan yang setiap sukunya merupakan perkalian dari suku sebelumnya dengan suatu konstanta tak nol yang disebut rasio. Rumus suku ke-n (Un) dalam barisan geometri dinyatakan sebagai berikut:

Un = a

r^(n-1)

di mana:* a adalah suku pertama

• r adalah rasio
• n adalah nomor urut suku

Sifat Barisan Geometri

Barisan geometri adalah barisan bilangan yang setiap suku setelah suku pertama diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio.

Rasio Barisan Geometri

Rasio barisan geometri adalah bilangan tetap yang digunakan untuk mengalikan suku sebelumnya untuk mendapatkan suku berikutnya. Rasio dilambangkan dengan r .

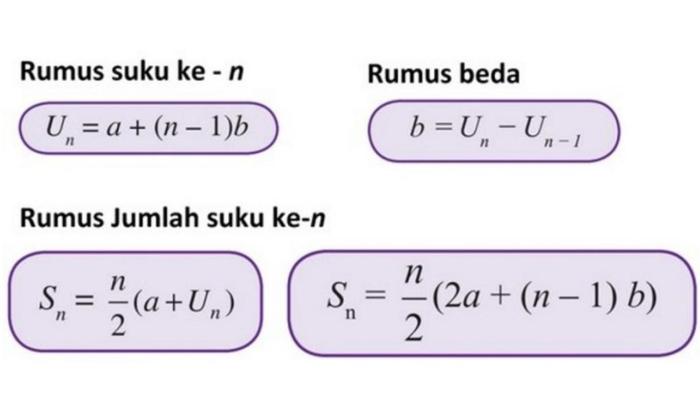
Rumus Barisan Geometri

Rumus untuk suku ke- n barisan geometri adalah:

U _n = a ₁ – r ^n-1

di mana:

• U_n adalah suku ke-n
• a₁ adalah suku pertama
• r adalah rasio
• n adalah nomor suku

Sifat-sifat Barisan Geometri

Barisan geometri memiliki beberapa sifat penting, antara lain:

• Setiap suku setelah suku pertama diperoleh dengan mengalikan suku sebelumnya dengan rasio.
• Rasio antara dua suku yang berurutan selalu sama.
• Jumlah suku hingga dari barisan geometri adalah:

  S _n = a ₁ – (1 – r ⁿ ) / (1 – r)

• Barisan geometri konvergen jika |r| < 1 dan divergen jika |r| ≥ 1.

Contoh Penerapan Barisan Geometri

Barisan geometri memiliki banyak aplikasi dalam kehidupan nyata, antara lain:

• Peluruhan radioaktif
• Pertumbuhan populasi
• Investasi dengan bunga majemuk

Contoh Soal dan Pembahasan

Contoh soal barisan geometri 5, 15, 45:

Diketahui barisan geometri 5, 15, 45, …, tentukan suku ke-5 dari barisan tersebut.

Pembahasan:

1. Tentukan rasio barisan dengan membagi suku kedua dengan suku pertama:

“`r = 15/5 = 3“`

2. Gunakan rumus suku ke-n barisan geometri untuk menentukan suku ke-5:

“`Un = a

r^(n-1)

“`

3. Dimana a adalah suku pertama dan n adalah nomor suku. Untuk suku ke-5, n = 5:

“`U5 = 5

3^(5-1)

“`

4. Hitung nilai U5:

“`U5 = 5

• 3^4 = 5
• 81 = 405

“`Jadi, suku ke-5 dari barisan geometri tersebut adalah 405.

Aplikasi Barisan Geometri

Barisan geometri memiliki berbagai aplikasi dalam kehidupan nyata. Berikut adalah beberapa contohnya:

Penerapan dalam Bidang Sains dan Teknologi

• Pertumbuhan Bakteri: Jumlah bakteri sering kali mengikuti barisan geometri, di mana setiap bakteri membelah menjadi dua bakteri baru dalam jangka waktu tertentu.
• Peluruhan Radioaktif: Inti atom radioaktif meluruh dengan kecepatan yang mengikuti barisan geometri, dengan waktu paruh yang konstan.
• Difraksi Cahaya: Pola difraksi cahaya melalui celah atau kisi mengikuti barisan geometri, dengan intensitas maksimum dan minimum yang berselang-seling.

Penerapan dalam Bidang Ekonomi dan Keuangan

• Suku Bunga Majemuk: Suku bunga majemuk dihitung menggunakan barisan geometri, di mana bunga ditambahkan ke pokok dan menghasilkan bunga lebih banyak pada periode berikutnya.
• Depresiasi Aset: Nilai aset tetap berkurang dengan kecepatan yang mengikuti barisan geometri, yang dikenal sebagai depresiasi.
• Pertumbuhan Penduduk: Dalam beberapa kasus, pertumbuhan populasi dapat mengikuti barisan geometri, di mana setiap generasi menghasilkan jumlah keturunan yang sama.

Penerapan dalam Bidang Sosial dan Budaya

• Penyebaran Informasi: Informasi dapat menyebar melalui jaringan sosial dengan kecepatan yang mengikuti barisan geometri, di mana setiap orang membagikan informasi kepada sejumlah teman.
• Efek Domino: Peristiwa kecil dapat memicu serangkaian peristiwa yang lebih besar, yang dapat mengikuti barisan geometri dalam hal intensitas atau dampak.
• Perkembangan Budaya: Beberapa aspek budaya, seperti bahasa dan tradisi, dapat berkembang dengan cara yang mengikuti barisan geometri, di mana generasi berikutnya membangun dan memodifikasi warisan yang ada.

Penutupan

Pembahasan mengenai barisan geometri 5, 15, dan 45 telah memberikan wawasan yang komprehensif tentang konsep, sifat, dan aplikasinya. Barisan geometri terbukti sebagai alat yang berharga dalam memecahkan berbagai permasalahan, dan pemahaman yang baik tentangnya sangat penting bagi siapa pun yang ingin menguasai matematika.

Jawaban yang Berguna

Apa perbedaan antara barisan geometri dan barisan aritmatika?

Barisan geometri memiliki beda yang sama pada rasio antar sukunya, sedangkan barisan aritmatika memiliki beda yang sama pada selisih antar sukunya.

Bagaimana cara menghitung suku ke-n dalam barisan geometri?

Gunakan rumus Un = a – r^(n-1), di mana a adalah suku pertama, r adalah rasio, dan n adalah nomor suku.

Apa saja sifat-sifat barisan geometri?

Jumlah n suku pertama barisan geometri adalah Sn = a – (1 – r^n) / (1 – r), jumlah tak hingga barisan geometri adalah a / (1 – r) jika |r|< 1, dan jumlah suku genap atau ganjil barisan geometri dapat dihitung dengan memisahkan suku-sukunya.