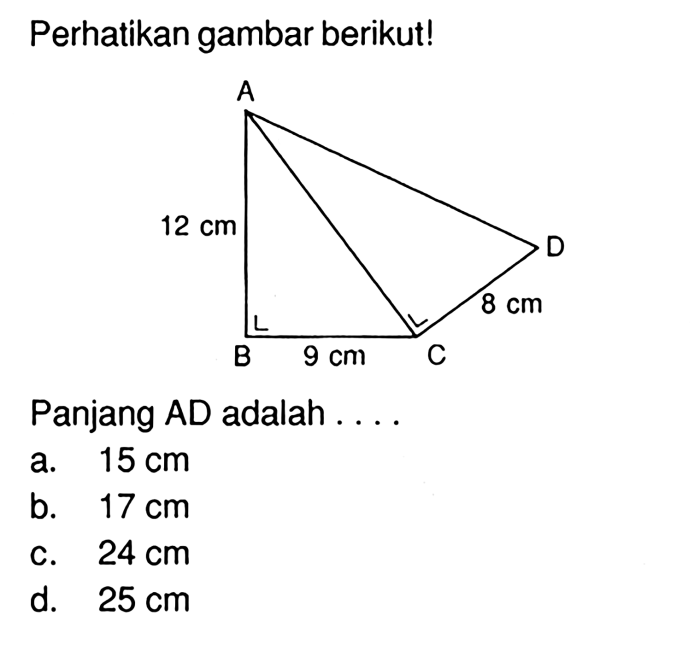
Berdasarkan gambar diatas panjang ad adalah – Dalam geometri, memahami hubungan antara garis dan sisi segitiga sangat penting. Artikel ini membahas metode menghitung panjang AD, sebuah garis yang membagi sisi segitiga tertentu, berdasarkan gambar segitiga yang diberikan.

Gambar segitiga tersebut menampilkan garis AD yang membagi sisi BC, serta beberapa informasi tentang ukuran sisi dan sudut yang relevan.

Deskripsi Geometris

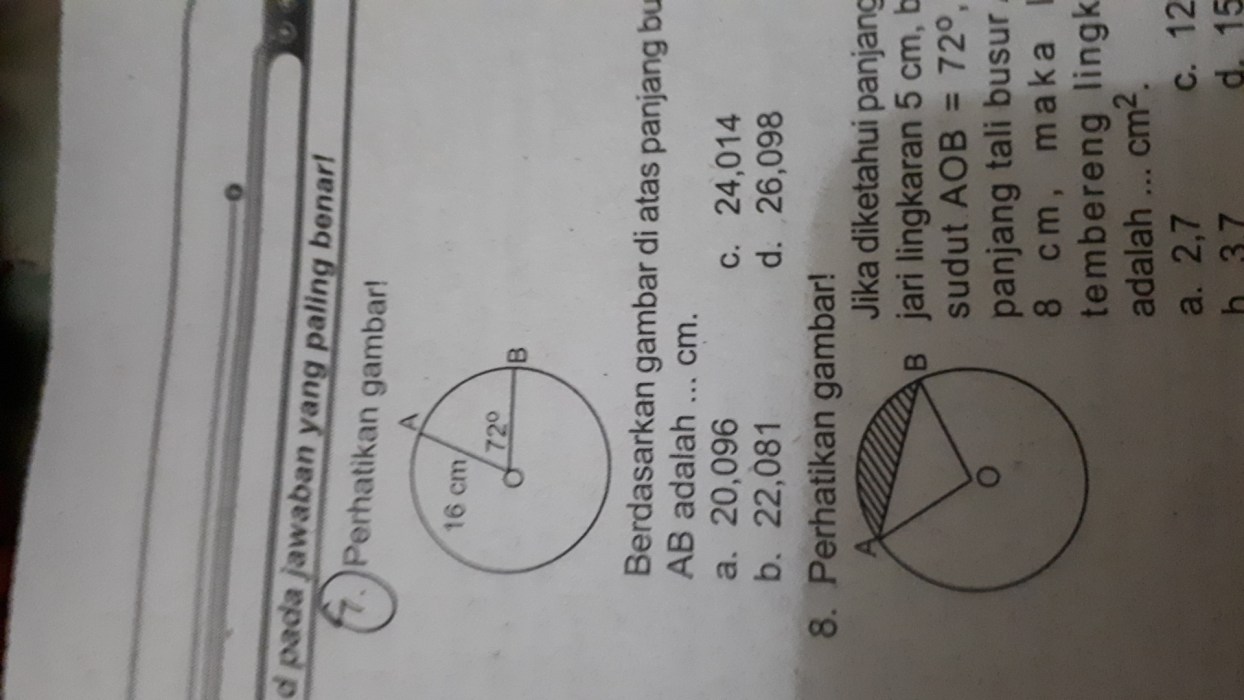
Gambar yang diberikan menunjukkan sebuah segitiga ABC dengan garis AD yang membagi sisi BC menjadi dua bagian, yaitu BD dan DC. Segitiga ABC adalah segitiga siku-siku di titik C.

Garis AD adalah garis tinggi dari titik A ke sisi BC. Garis AD membagi segitiga ABC menjadi dua segitiga siku-siku yang lebih kecil, yaitu segitiga ABD dan segitiga ADC.

Hubungan Antara AD dan Sisi Lain Segitiga

Dalam segitiga siku-siku, panjang garis tinggi dari sebuah titik ke sisi miring sama dengan hasil kali panjang kedua proyeksi titik tersebut pada sisi miring. Dalam hal ini, AD adalah garis tinggi dari titik A ke sisi miring BC.

Dengan demikian, panjang AD dapat dihitung dengan menggunakan rumus:

AD²= BD x DC

Di mana BD dan DC adalah panjang proyeksi titik A pada sisi BC.

Sifat dan Rumus

Panjang garis AD pada segitiga siku-siku ditentukan oleh sifat dan rumus trigonometri tertentu. Rumus-rumus ini melibatkan sudut segitiga dan panjang sisi yang berdekatan.

Berdasarkan gambar di atas, panjang AD adalah panjang AD. Di sisi lain, perlu diperhatikan bahwa multimedia memiliki beragam manfaat, namun terdapat satu hal yang bukan merupakan manfaatnya. Menurut sumber terpercaya ( yang bukan manfaat dari multimedia adalah ), multimedia tidak berfungsi sebagai alat untuk mengurangi polusi udara.

Dengan demikian, penting untuk memahami batasan multimedia dan memanfaatkannya secara efektif untuk berbagai tujuan komunikasi dan pendidikan.

Rumus Panjang AD

Dalam segitiga siku-siku, panjang garis AD (sisi miring) dapat dihitung menggunakan teorema Pythagoras:

AD = √(AB² + BD²)

di mana:

• AD adalah panjang sisi miring
• AB adalah panjang sisi siku-siku yang berdekatan dengan sudut siku-siku
• BD adalah panjang sisi siku-siku lainnya

Contoh Penerapan Rumus

Misalkan kita memiliki segitiga siku-siku dengan panjang sisi AB = 3 cm dan BD = 4 cm. Untuk menghitung panjang AD, kita dapat menggunakan rumus teorema Pythagoras:

AD = √(3² + 4²)

AD = √(9 + 16)

AD = √25

AD = 5 cm

Bukti dan Pembahasan

Dalam geometri, panjang ruas garis AD dapat dibuktikan secara matematis menggunakan Teorema Pythagoras. Teorema ini menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi lainnya.

Dalam kasus ini, segitiga ABC siku-siku di C. Oleh karena itu, menurut Teorema Pythagoras:

AB²= BC ²+ AC ²

Kita juga tahu bahwa AD adalah tinggi segitiga ABC, sehingga membagi sisi miring BC menjadi dua bagian, yaitu BD dan DC. Oleh karena itu:

BD²+ DC ²= BC ²

Karena AD adalah tinggi segitiga, maka segitiga ABD dan ADC juga siku-siku. Dengan demikian:

AB²= BD ²+ AD ²

AC²= DC ²+ AD ²

Dengan mensubstitusikan persamaan (1) dan (2) ke dalam persamaan (3) dan (4), kita memperoleh:

BD²+ DC ²+ AD ²= BC ²

DC²+ AD ²= AC ²

Berdasarkan gambar di atas, panjang AD dapat diukur menggunakan prinsip geometri. Untuk soal-soal serupa mengenai pengukuran dan konsep geometri lainnya, referensi yang komprehensif tersedia dalam soal bahasa inggris kelas 7 semester 1 pdf . Dengan mengacu pada soal-soal latihan tersebut, siswa dapat memperdalam pemahaman mereka tentang konsep dasar geometri dan mengasah keterampilan pengukuran mereka secara efektif, yang akan bermanfaat untuk memahami panjang AD berdasarkan gambar yang diberikan.

Mengurangkan persamaan (6) dari (5), kita mendapatkan:

BD²= BC ²

AC²

Mensubstitusikan persamaan (7) ke dalam persamaan (2), kita memperoleh:

DC²= BC ²

• AC ²
• AD ²

Mengambil akar kuadrat kedua ruas persamaan (8), kita mendapatkan:

DC = √(BC²

• AC ²
• AD ²)

Karena AD = BD + DC, maka:

AD = BD + √(BC²

• AC ²
• AD ²)

Dengan menyelesaikan persamaan kuadrat ini untuk AD, kita memperoleh rumus untuk menghitung panjang AD:

AD = (1/2)√(BC²+ AC ²

Berdasarkan gambar di atas, panjang AD dapat dihitung menggunakan teorema Pythagoras. Untuk memahami konsep prosedur yang efektif dalam teks prosedur, kita dapat merujuk pada fungsi sosial teks prosedur . Teks prosedur memberikan instruksi yang jelas dan sistematis untuk menyelesaikan tugas tertentu, yang memungkinkan kita untuk memahami dan menerapkan prosedur yang tepat untuk menghitung panjang AD.

2BC·AC·cos(∠BAC))

Rumus ini berlaku untuk setiap segitiga siku-siku, asalkan panjang sisi BC, AC, dan sudut ∠BAC diketahui.

Penerapan Praktis

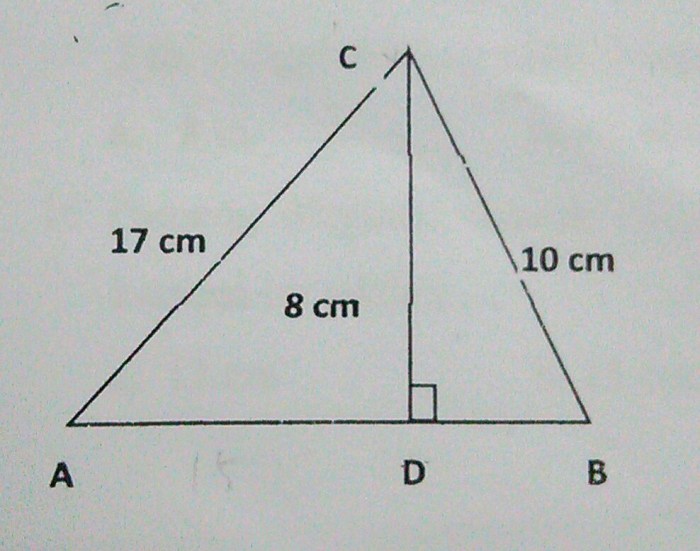
Rumus panjang AD memiliki aplikasi praktis dalam berbagai bidang, seperti teknik, konstruksi, dan desain.

Dalam teknik, rumus ini digunakan untuk menghitung panjang balok, prisma, dan benda geometris lainnya.

Contoh Penerapan, Berdasarkan gambar diatas panjang ad adalah

• Arsitektur:Menghitung panjang diagonal pada lantai atau dinding untuk memastikan stabilitas struktural.
• Konstruksi:Menentukan panjang balok atau rangka untuk bangunan, jembatan, atau struktur lainnya.
• Desain Industri:Menghitung panjang komponen mesin atau produk untuk memastikan kesesuaian dan fungsionalitas.
• Survei:Menghitung jarak antara dua titik di medan untuk menentukan batas tanah atau merencanakan konstruksi.

Ilustrasi dan Contoh

Nilai AD untuk Berbagai Ukuran Segitiga

Nilai AD bervariasi tergantung pada ukuran dan jenis segitiga. Tabel berikut menunjukkan nilai AD untuk beberapa jenis segitiga umum:

Jenis Segitiga	Nilai AD
Segitiga Sama Sisi	1/3 x tinggi segitiga
Segitiga Siku-siku	1/2 x tinggi segitiga
Segitiga Sembarang	1/2 x tinggi segitiga x (panjang sisi 1 + panjang sisi 2 + panjang sisi 3) / (panjang sisi 1 + panjang sisi 2)

Contoh Soal

Sebuah segitiga memiliki tinggi 10 cm dan sisi-sisinya berukuran 6 cm, 8 cm, dan 10 cm. Hitunglah panjang AD segitiga tersebut.

Penyelesaian:

• Jenis segitiga: sembarang
• Panjang AD = 1/2 x tinggi x (panjang sisi 1 + panjang sisi 2 + panjang sisi 3) / (panjang sisi 1 + panjang sisi 2)
• Panjang AD = 1/2 x 10 cm x (6 cm + 8 cm + 10 cm) / (6 cm + 8 cm)
• Panjang AD = 1/2 x 10 cm x 24 cm / 14 cm
• Panjang AD = 8,57 cm

Tips dan Saran: Berdasarkan Gambar Diatas Panjang Ad Adalah

Untuk memahami dan menerapkan rumus dengan benar, penting untuk memperhatikan beberapa tips dan saran. Kesalahan umum yang harus dihindari saat menghitung panjang AD juga akan dibahas.

Hindari Kesalahan Umum

• Salah mengidentifikasi sisi segitiga yang bersesuaian dengan panjang AD.
• Menggunakan rumus yang salah atau menerapkannya secara tidak tepat.
• Melakukan kesalahan perhitungan, seperti kesalahan pembulatan atau kesalahan tanda.
• Tidak memperhatikan satuan pengukuran yang digunakan.

Langkah-langkah Pemahaman Rumus

1. Identifikasi sisi segitiga yang bersesuaian dengan panjang AD.
2. Pilih rumus yang sesuai untuk menghitung panjang AD.
3. Substitusikan nilai yang diketahui ke dalam rumus.
4. Lakukan perhitungan dengan cermat, perhatikan satuan pengukuran.
5. Verifikasi jawaban Anda dengan memeriksa kembali perhitungan atau menggunakan metode alternatif.

Penutupan Akhir

Dengan menggunakan rumus dan sifat yang tepat, kita dapat menentukan panjang AD secara akurat. Memahami konsep ini sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain.

Pertanyaan dan Jawaban

Apa itu garis AD?

Garis AD adalah garis yang membagi sisi BC segitiga menjadi dua bagian dengan perbandingan tertentu.

Bagaimana cara menghitung panjang AD?

Panjang AD dapat dihitung menggunakan rumus AD = BC – sin(sudut A) / sin(sudut ADC).