Dalam dunia fisika, mengamati gerakan benda di bawah pengaruh gaya merupakan aspek fundamental. Salah satu fenomena menarik yang telah dipelajari secara ekstensif adalah pergerakan bola yang menggelinding di bidang miring. Analisis fenomena ini tidak hanya memberikan wawasan teoretis yang berharga, tetapi juga memiliki aplikasi praktis yang signifikan dalam berbagai bidang.
Konsep dasar yang mendasari gerakan bola di bidang miring melibatkan hukum gerak Newton, yang menggambarkan hubungan antara gaya, massa, dan percepatan. Memahami prinsip-prinsip ini sangat penting untuk memprediksi dan menganalisis pergerakan bola, termasuk percepatan, kecepatan, dan jarak yang ditempuhnya.
Konsep Dasar
Bola yang menggelinding di bidang miring merupakan contoh penerapan hukum gerak Newton. Ketika bola dilepas dari suatu titik di bidang miring, gaya gravitasi menarik bola ke bawah sehingga bola mengalami percepatan dan bergerak menuruni bidang miring.Gerakan bola pada bidang miring dapat dianalisis menggunakan konsep percepatan, kecepatan, dan jarak yang ditempuh.
Percepatan bola disebabkan oleh gaya gravitasi yang bekerja pada bola, yang besarnya bergantung pada sudut kemiringan bidang miring. Kecepatan bola meningkat seiring dengan waktu, dan jarak yang ditempuh bola berbanding lurus dengan kuadrat waktu.Persamaan gerak yang dapat digunakan untuk menganalisis gerakan bola pada bidang miring adalah:“`v = u + ats = ut + 1/2at^2“`di mana:* v adalah kecepatan akhir bola
- u adalah kecepatan awal bola (biasanya 0)
- a adalah percepatan bola
- t adalah waktu
- s adalah jarak yang ditempuh bola
Faktor yang Mempengaruhi Gerakan

Gerakan bola pada bidang miring dipengaruhi oleh beberapa faktor, antara lain:
Sudut Kemiringan Bidang
- Sudut kemiringan menentukan besarnya komponen gaya gravitasi yang bekerja pada bola.
- Semakin besar sudut kemiringan, semakin besar komponen gaya gravitasi, sehingga semakin besar percepatan dan kecepatan bola.
Massa Bola
- Massa bola memengaruhi inersianya.
- Bola dengan massa lebih besar memiliki inersia lebih besar, sehingga membutuhkan gaya yang lebih besar untuk mempercepat atau memperlambatnya.
- Dengan sudut kemiringan yang sama, bola dengan massa lebih besar akan bergerak lebih lambat daripada bola dengan massa lebih kecil.
Koefisien Gesekan
- Koefisien gesekan adalah ukuran gesekan antara bola dan bidang miring.
- Semakin besar koefisien gesekan, semakin besar gaya gesek yang bekerja pada bola, sehingga semakin kecil percepatan dan kecepatan bola.
Sebagai contoh, jika sudut kemiringan bidang diperbesar, bola akan bergerak lebih cepat karena komponen gaya gravitasi yang lebih besar. Sebaliknya, jika massa bola diperbesar, bola akan bergerak lebih lambat karena inersianya yang lebih besar. Terakhir, jika koefisien gesekan diperbesar, bola akan bergerak lebih lambat karena gaya gesek yang lebih besar.
Cara Menghitung Gerakan Bola
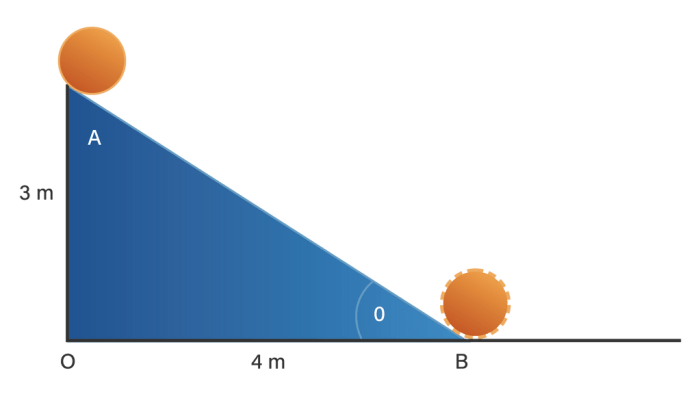
Menghitung gerakan bola yang menggelinding di bidang miring melibatkan beberapa langkah dan perhitungan.
Menghitung Percepatan Bola
Untuk menghitung percepatan bola yang menggelinding di bidang miring, ikuti langkah-langkah berikut:
- Identifikasi sudut kemiringan bidang miring (θ).
- Gunakan persamaan berikut untuk menghitung percepatan karena gravitasi (g): g = 9,81 m/s².
- Hitung percepatan bola (a) menggunakan persamaan berikut: a = g
sin(θ).
| Variabel | Deskripsi | Persamaan |
|---|---|---|
| θ | Sudut kemiringan bidang miring | |
| g | Percepatan karena gravitasi | g = 9,81 m/s² |
| a | Percepatan bola | a = g
|
Contoh Perhitungan:
Sebuah bola menggelinding di bidang miring dengan sudut kemiringan 30°. Hitung percepatan bola.
- θ = 30°
- g = 9,81 m/s²
- a = g
- sin(θ) = 9,81 m/s²
- sin(30°) ≈ 4,91 m/s²
Oleh karena itu, percepatan bola yang menggelinding di bidang miring adalah sekitar 4,91 m/s².
Aplikasi Praktis

Prinsip-prinsip gerakan bola di bidang miring memiliki aplikasi luas dalam berbagai bidang kehidupan nyata, termasuk teknik, olahraga, dan transportasi. Memahami prinsip-prinsip ini sangat penting untuk merancang dan mengoperasikan sistem yang melibatkan benda bergerak di sepanjang bidang miring.
Teknik
Dalam teknik, prinsip gerakan bola di bidang miring digunakan dalam desain berbagai struktur dan mesin. Misalnya, dalam pembangunan jalan dan rel kereta api, kemiringan permukaan sangat penting untuk memastikan drainase yang memadai dan stabilitas kendaraan. Selain itu, prinsip ini digunakan dalam desain konveyor, elevator, dan sistem pengangkutan lainnya yang melibatkan pergerakan benda di sepanjang bidang miring.
Olahraga
Dalam olahraga, gerakan bola di bidang miring dimanfaatkan dalam berbagai permainan dan aktivitas. Dalam bowling, misalnya, pemain harus memperhitungkan kemiringan jalur untuk mengarahkan bola secara akurat menuju pin. Di bidang golf, pemain menggunakan kemiringan lapangan untuk mengendalikan arah dan jarak pukulan mereka.
Transportasi
Dalam transportasi, prinsip gerakan bola di bidang miring digunakan dalam desain dan pengoperasian berbagai kendaraan. Dalam kendaraan bermotor, rem bekerja dengan mengubah gerakan bola di bidang miring untuk memperlambat atau menghentikan kendaraan. Kemiringan jalan juga mempengaruhi kecepatan dan efisiensi kendaraan.
“Pemahaman yang mendalam tentang gerakan bola di bidang miring sangat penting untuk merancang dan mengoperasikan sistem yang melibatkan benda bergerak di sepanjang bidang miring dengan aman dan efisien.”
Kesalahan Umum dan Solusi

Analisis gerak bola pada bidang miring dapat menimbulkan kesalahan umum yang dapat mempengaruhi akurasi hasil. Memahami dan mengatasi kesalahan ini sangat penting untuk meningkatkan ketepatan analisis.
Kesalahan dalam Menentukan Koefisien Gesek
- Mengabaikan koefisien gesek statis dan kinetik.
- Menggunakan nilai koefisien gesek yang tidak sesuai dengan permukaan atau kondisi bola.
- Mengasumsikan koefisien gesek konstan sepanjang bidang miring.
Solusi:
- Tentukan koefisien gesek statis dan kinetik secara terpisah melalui eksperimen atau data yang dapat diandalkan.
- Pilih nilai koefisien gesek yang sesuai dengan material permukaan dan kondisi bola.
- Pertimbangkan variasi koefisien gesek di sepanjang bidang miring karena perubahan kemiringan atau kondisi permukaan.
Kesalahan dalam Menganalisis Percepatan
- Mengabaikan percepatan karena gravitasi.
- Mengasumsikan percepatan konstan sepanjang gerak bola.
- Tidak memperhitungkan komponen percepatan tegak lurus bidang miring.
Solusi:
- Sertakan percepatan karena gravitasi dalam persamaan gerak.
- Pertimbangkan kemungkinan percepatan yang berubah-ubah karena faktor seperti gesekan atau perubahan kemiringan.
- Analisis komponen percepatan tegak lurus bidang miring untuk menentukan gaya normal.
Kesalahan dalam Menganalisis Gaya
- Mengabaikan gaya gesek.
- Menggunakan arah gaya gesek yang salah.
- Tidak memperhitungkan gaya tegak lurus bidang miring.
Solusi:
- Sertakan gaya gesek dalam persamaan gerak sesuai dengan arah dan besarnya yang benar.
- Tentukan arah gaya gesek dengan benar, berlawanan dengan arah gerak bola.
- Analisis gaya tegak lurus bidang miring untuk menentukan gaya normal dan memperhitungkan gesekan statis.
Ringkasan Akhir
Secara keseluruhan, mempelajari gerakan bola di bidang miring memberikan pemahaman yang mendalam tentang prinsip-prinsip fisika yang mendasar. Selain itu, penerapan praktisnya yang luas dalam berbagai bidang menyoroti pentingnya memahami fenomena ini. Dengan menguasai konsep dan aplikasi ini, kita dapat lebih menghargai kompleksitas dunia fisik di sekitar kita dan memanfaatkan pengetahuan ini untuk memecahkan masalah dan menciptakan solusi inovatif.
Ringkasan FAQ
Apa faktor yang memengaruhi kecepatan bola yang menggelinding di bidang miring?
Sudut kemiringan bidang, massa bola, dan koefisien gesekan antara bola dan permukaan bidang.
Bagaimana cara menghitung percepatan bola yang menggelinding di bidang miring?
Gunakan persamaan: percepatan = percepatan gravitasi – sinus sudut kemiringan.
Apa saja aplikasi praktis dari prinsip-prinsip gerakan bola di bidang miring?
Dalam teknik sipil (membangun jalan dan jembatan), olahraga (mendesain landasan pacu ski), dan transportasi (merancang sistem pengereman).
