Simpangan kuartil, ukuran penyebaran data, memainkan peran penting dalam statistik dan analisis data. Panduan komprehensif ini akan menguraikan cara mencari simpangan kuartil data kelompok, faktor-faktor yang memengaruhinya, dan aplikasi praktisnya di berbagai bidang.
Pengertian Simpangan Kuartil
Simpangan kuartil adalah ukuran penyebaran data yang membagi kumpulan data menjadi empat bagian yang sama, yaitu kuartil pertama (Q1), kuartil kedua (Q2 atau median), kuartil ketiga (Q3), dan kuartil keempat (Q4). Simpangan kuartil digunakan untuk mengukur variabilitas data dan membandingkan penyebaran beberapa kumpulan data.
Rumus Simpangan Kuartil
Simpangan kuartil dapat dihitung menggunakan rumus berikut:
IQR = Q3
Q1
Simpangan kuartil, ukuran variabilitas data kelompok, dapat dihitung dengan mengurangi kuartil atas dan bawah. Bentuk baku dari bilangan 0,00000743 adalah 7,43 x 10 -6. Dengan memahami bentuk baku ini, kita dapat memperoleh pemahaman yang lebih baik tentang besarnya bilangan dan implikasinya dalam konteks statistik, seperti dalam menghitung simpangan kuartil.
di mana:
- IQR adalah simpangan kuartil
- Q3 adalah kuartil ketiga
- Q1 adalah kuartil pertama
Interpretasi Simpangan Kuartil
Simpangan kuartil dapat diinterpretasikan sebagai berikut:
- IQR yang kecil menunjukkan bahwa data tersebar secara sempit di sekitar median.
- IQR yang besar menunjukkan bahwa data tersebar secara luas di sekitar median.
Penggunaan Simpangan Kuartil
Simpangan kuartil memiliki beberapa penggunaan dalam statistik, di antaranya:
- Membandingkan variabilitas beberapa kumpulan data
- Mengidentifikasi outlier atau data yang tidak biasa
- Membuat box plot untuk memvisualisasikan distribusi data
Langkah-Langkah Mencari Simpangan Kuartil Data Kelompok
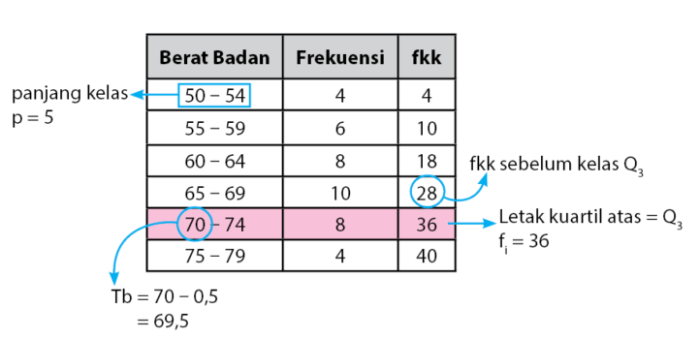
Simpangan kuartil adalah ukuran penyebaran data yang menunjukkan perbedaan antara kuartil ketiga (Q3) dan kuartil pertama (Q1). Langkah-langkah untuk menghitung simpangan kuartil data kelompok adalah sebagai berikut:
Membuat Tabel Data Kelompok
Buat tabel yang berisi nilai data yang diurutkan dari terkecil ke terbesar, serta nilai kuartilnya (Q1, Q2, Q3).
Menghitung Nilai Kuartil
Hitung nilai Q1, Q2, dan Q3 menggunakan rumus berikut:
- Q1 = nilai pada posisi (n+1)/4, dengan n adalah jumlah data
- Q2 = nilai pada posisi (n+1)/2
- Q3 = nilai pada posisi 3(n+1)/4
Menghitung Simpangan Kuartil
Hitung simpangan kuartil menggunakan rumus:
Simpangan Kuartil = Q3
Untuk menghitung simpangan kuartil data kelompok, pertama-tama kita perlu mengurutkan data dari nilai terkecil ke terbesar. Selanjutnya, kita dapat menghitung kuartil pertama (Q1) sebagai median dari setengah bagian data terendah, dan kuartil ketiga (Q3) sebagai median dari setengah bagian data tertinggi.
Simpangan kuartil, yang merupakan ukuran variabilitas, kemudian dapat dihitung sebagai perbedaan antara Q3 dan Q1. Sama seperti perasaan sedih yang mendalam ketika sahabat terbaik kita meninggalkan kita, i sad when my best friend left me yesterday , simpangan kuartil memberikan wawasan tentang penyebaran data, dengan nilai yang lebih besar menunjukkan variasi yang lebih luas.
Q1
Faktor-Faktor yang Mempengaruhi Simpangan Kuartil: Cara Mencari Simpangan Kuartil Data Kelompok
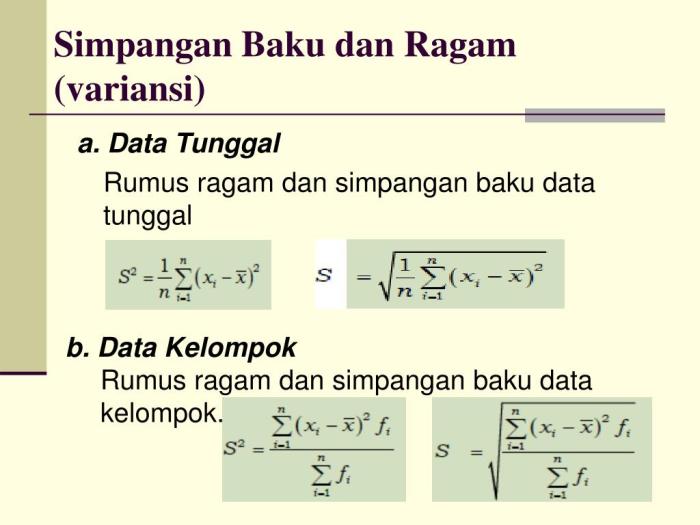
Simpangan kuartil, yang juga dikenal sebagai kisaran interkuartil, merupakan ukuran variabilitas yang digunakan untuk menggambarkan penyebaran data. Terdapat beberapa faktor yang dapat memengaruhi nilai simpangan kuartil, antara lain:
Ukuran Sampel
Ukuran sampel mengacu pada jumlah pengamatan dalam suatu kumpulan data. Secara umum, semakin besar ukuran sampel, semakin kecil nilai simpangan kuartil. Hal ini karena sampel yang lebih besar cenderung lebih mewakili populasi, sehingga penyebaran datanya akan lebih merata.
Distribusi Data
Distribusi data mengacu pada bentuk penyebaran data. Distribusi data yang simetris akan memiliki simpangan kuartil yang lebih kecil dibandingkan dengan distribusi data yang miring atau berpuncak. Misalnya, distribusi data normal akan memiliki simpangan kuartil yang lebih kecil dibandingkan dengan distribusi data yang miring ke kanan.
Adanya Titik Ekstrem, Cara mencari simpangan kuartil data kelompok
Titik ekstrem adalah nilai data yang sangat jauh dari nilai rata-rata. Kehadiran titik ekstrem dapat meningkatkan nilai simpangan kuartil. Hal ini karena titik ekstrem dapat memperlebar rentang data, sehingga meningkatkan perbedaan antara kuartil ketiga dan pertama.
Untuk menentukan simpangan kuartil data kelompok, terlebih dahulu diurutkan data dari yang terkecil hingga terbesar. Kuartal pertama (Q1) adalah nilai yang memisahkan 25% data terkecil, sementara kuartal ketiga (Q3) memisahkan 75% data terkecil. Simpangan kuartil (IQR) dihitung sebagai selisih antara Q3 dan Q1.
Sebagai referensi lebih lanjut mengenai kebudayaan Indonesia, teks non fiksi tentang kebudayaan indonesia dapat menjadi sumber bacaan yang komprehensif. IQR merupakan ukuran penyebaran data yang robust terhadap data ekstrem dan banyak digunakan dalam analisis statistik.
Interpretasi Hasil Simpangan Kuartil

Menafsirkan nilai simpangan kuartil sangat penting untuk memahami penyebaran data. Nilai simpangan kuartil menunjukkan perbedaan antara kuartil atas (Q3) dan kuartil bawah (Q1).
Simpangan kuartil yang tinggi menunjukkan bahwa data tersebar luas, dengan perbedaan yang signifikan antara nilai terkecil dan terbesar. Sebaliknya, simpangan kuartil yang rendah menunjukkan bahwa data terdistribusi secara merata, dengan nilai-nilai yang mengelompok di sekitar nilai tengah.
Penafsiran Penyebaran Data
- Penyebaran Data Tinggi:Simpangan kuartil yang tinggi menunjukkan penyebaran data yang luas. Ini berarti bahwa ada perbedaan yang signifikan antara nilai minimum dan maksimum, dan sebagian besar data berada di luar rentang nilai tengah.
- Penyebaran Data Rendah:Simpangan kuartil yang rendah menunjukkan penyebaran data yang sempit. Ini berarti bahwa nilai-nilai data terdistribusi secara merata di sekitar nilai tengah, dengan hanya sedikit variasi antara nilai terkecil dan terbesar.
Aplikasi Simpangan Kuartil dalam Berbagai Bidang

Simpangan kuartil merupakan ukuran penyebaran data yang banyak digunakan dalam berbagai bidang. Berikut beberapa aplikasi simpangan kuartil:
Statistik
Simpangan kuartil digunakan untuk:
- Mengukur variabilitas distribusi data.
- Membandingkan variabilitas antar distribusi data yang berbeda.
- Mengidentifikasi outlier dalam suatu kumpulan data.
Ilmu Data
Simpangan kuartil digunakan untuk:
- Mengeksplorasi dan memahami distribusi data.
- Membuat visualisasi data yang informatif, seperti box plot.
- Mengelompokkan data berdasarkan kemiripan dalam variabilitas.
Bisnis
Simpangan kuartil digunakan untuk:
- Menganalisis kinerja bisnis dan mengidentifikasi tren.
- Membandingkan kinerja bisnis dengan pesaing.
- Membuat keputusan berdasarkan data tentang alokasi sumber daya dan strategi bisnis.
Ringkasan Penutup

Dengan memahami cara mencari simpangan kuartil, kita dapat memperoleh wawasan yang berharga tentang penyebaran data, membuat keputusan yang tepat, dan meningkatkan pemahaman kita tentang berbagai fenomena dunia nyata.
Pertanyaan Umum (FAQ)
Apa tujuan penggunaan simpangan kuartil?
Simpangan kuartil digunakan untuk mengukur penyebaran data, menunjukkan seberapa bervariasinya data dari nilai tengah.
Bagaimana cara menafsirkan nilai simpangan kuartil yang tinggi?
Nilai simpangan kuartil yang tinggi menunjukkan bahwa data tersebar luas, dengan perbedaan yang signifikan antara nilai-nilai data.
