Integral tentu adalah konsep fundamental dalam kalkulus yang memungkinkan kita menghitung luas, volume, dan berbagai besaran lainnya. Dengan memahami metode dan teknik yang tepat, mengerjakan integral tentu menjadi proses yang dapat dikelola.

Dalam panduan ini, kita akan membahas dasar-dasar integral tentu, berbagai metode integrasi, aplikasinya dalam menghitung luas dan volume, serta teknik pemecahan masalah yang efektif. Dengan sumber daya dan referensi yang disediakan, Anda akan memiliki semua yang Anda perlukan untuk menguasai seni mengerjakan integral tentu.

Pemahaman Dasar

Konsep integral tentu merupakan dasar dari kalkulus integral, yang merupakan cabang matematika yang mempelajari luas daerah, volume benda, dan panjang kurva.

Integral tentu dari suatu fungsi f(x) pada interval [a, b] didefinisikan sebagai luas daerah yang terletak di bawah grafik fungsi f(x) dan di atas sumbu x pada interval tersebut.

Notasi dan Terminologi

• ∫[a, b] f(x) dx: notasi integral tentu dari fungsi f(x) pada interval [a, b].
• a: batas bawah integral.
• b: batas atas integral.
• f(x): fungsi yang akan diintegralkan.
• dx: simbol diferensial yang menunjukkan variabel integrasi.

Metode Integral Tentu

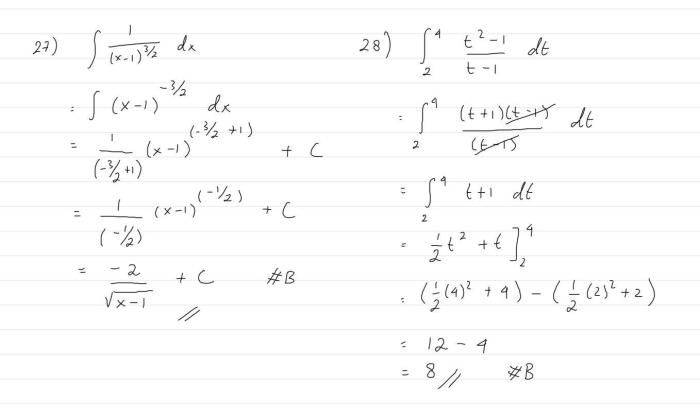
Integral tentu merupakan metode yang digunakan untuk menentukan luas daerah di bawah kurva fungsi dalam suatu interval. Ada beberapa metode untuk menghitung integral tentu, di antaranya:

Metode Integral Riemann

Metode Integral Riemann membagi interval menjadi subinterval yang sangat kecil, dan menghitung luas persegi panjang yang dibatasi oleh kurva fungsi dan sumbu x untuk setiap subinterval. Luas daerah di bawah kurva kemudian dihitung sebagai jumlah luas semua persegi panjang tersebut.

Metode Integral Trapezoidal

Metode Integral Trapezoidal menghampiri luas daerah di bawah kurva dengan menggunakan trapesium. Interval dibagi menjadi subinterval, dan luas trapesium yang dibatasi oleh kurva fungsi dan sumbu x untuk setiap subinterval dihitung. Luas daerah di bawah kurva kemudian dihitung sebagai jumlah luas semua trapesium tersebut.

Contoh Penerapan Metode Integral Trapezoidal

Sebagai contoh, misalkan kita ingin menghitung luas daerah di bawah kurva fungsi f(x) = x^2 pada interval [0, 2]. Kita dapat membagi interval menjadi n subinterval dengan lebar Δx = 2/n.Luas trapesium untuk subinterval ke-i diberikan oleh:“`(Δx/2)

(f(x_(i-1)) + f(x_i))

“`Dengan x_i = i

Δx.

Luas daerah di bawah kurva kemudian dihitung sebagai:“`∫[0, 2] x^2 dx ≈ (Δx/2)

Σ[i=1 to n] (f(x_(i-1)) + f(x_i))

“`Dengan n yang cukup besar, nilai aproksimasi ini akan mendekati nilai integral tentu yang sebenarnya.

Aplikasi Integral Tentu

Integral tentu memiliki berbagai aplikasi penting dalam matematika, fisika, dan teknik. Beberapa penerapannya yang paling umum meliputi:

Luas Daerah

Integral tentu dapat digunakan untuk menghitung luas daerah yang dibatasi oleh kurva dan sumbu koordinat. Rumus untuk luas daerah di bawah kurva y = f(x) antara titik a dan b diberikan oleh:

∫[a, b] f(x) dx

Volume Benda Putar

Integral tentu juga digunakan untuk menghitung volume benda putar yang dihasilkan ketika suatu daerah diputar mengelilingi sumbu. Rumus untuk volume benda putar yang dihasilkan oleh daerah yang dibatasi oleh kurva y = f(x) antara titik a dan b ketika diputar mengelilingi sumbu x adalah:

π∫[a, b] [f(x)] ² dx

Aplikasi dalam Fisika dan Teknik

Integral tentu memiliki banyak aplikasi dalam fisika dan teknik, seperti:

• Menghitung kerja yang dilakukan oleh gaya
• Menghitung pusat massa suatu benda
• Menghitung momen inersia suatu benda
• Menghitung fluks suatu medan

Teknik Pemecahan Masalah

Integral tentu merupakan teknik penting dalam kalkulus yang digunakan untuk menghitung luas daerah, volume benda, dan banyak aplikasi lainnya. Teknik pemecahan masalah memainkan peran penting dalam menyederhanakan dan menyelesaikan integral tentu yang kompleks.

Teknik Pemecahan Masalah Integral Tentu

Terdapat beberapa teknik pemecahan masalah yang dapat digunakan untuk integral tentu:

• Substitusi: Menggantikan variabel dalam integral dengan variabel baru untuk menyederhanakan ekspresi.
• Integrasi per bagian: Memecah integral menjadi dua bagian dan mengintegrasikan satu bagian menggunakan aturan pangkat.
• Integrasi parsial: Membagi integral menjadi dua bagian dan mengintegrasikan satu bagian menggunakan aturan pangkat dan satu bagian lainnya menggunakan teknik substitusi.
• Dekomposisi: Membagi integral menjadi beberapa bagian yang lebih sederhana dan mengintegrasikan setiap bagian secara terpisah.

Tips dan Trik

Selain teknik pemecahan masalah, terdapat beberapa tips dan trik yang dapat menyederhanakan integral yang kompleks:

• Faktorisasi: Memfaktorkan ekspresi integral untuk mengidentifikasi integral yang lebih sederhana.
• Ekspansi: Mengekspansi ekspresi integral menggunakan rumus trigonometri atau identitas aljabar.
• Pemisahan: Memisahkan integral menjadi dua atau lebih integral yang lebih sederhana.
• Perubahan batas: Mengubah batas integrasi untuk menyederhanakan ekspresi integral.

Contoh Langkah demi Langkah

Sebagai contoh, perhatikan integral:

∫ (x ² + 2x + 1) dx

Menggunakan teknik substitusi dengan u = x ² + 2x + 1, diperoleh:

∫ (u

1) du

Yang dapat diintegrasikan langsung menjadi:

(u ² /2)

u + C

Mengganti kembali u dengan x ² + 2x + 1, diperoleh solusi akhir:

(x ² + 2x + 1) ² /2

(x ² + 2x + 1) + C

Sumber Daya dan Referensi

Untuk mempelajari integral tentu lebih lanjut, tersedia berbagai sumber daya dan referensi yang dapat membantu:

• Sumber Daya Online:
  • Integral Calculus
    – Khan Academy: https://www.khanacademy.org/math/calculus-1/calculus-intro/x2eef969c74e0d802:derivatives_and_integrals/v/introduction-to-integral-calculus
  • Integral Calculus
    – Coursera: https://www.coursera.org/specializations/integral-calculus
  • Integral Calculus
    – MIT OpenCourseWare: https://ocw.mit.edu/courses/mathematics/18-02-calculus-ii-fall-2007/
• Buku Teks:
  • Calculus: Early Transcendentals
    – James Stewart
  • Calculus: A Complete Course
    – Robert A. Adams
  • Calculus
    – Michael Spivak
• Kutipan Ahli:
  

  Integral tentu adalah dasar dari semua matematika terapan.

  Perangkat Lunak dan Alat:

  • Wolfram Alpha: https://www.wolframalpha.com/
  • Integral Calculator: https://www.integral-calculator.com/

  • Maple: https://www.maplesoft.com/

Ringkasan Akhir

Integral tentu adalah alat yang ampuh yang telah merevolusi banyak bidang sains dan teknik. Memahami cara mengerjakannya secara efektif sangat penting untuk kesuksesan di berbagai disiplin ilmu.

Dengan mengikuti langkah-langkah yang diuraikan dalam panduan ini, Anda dapat mengembangkan keterampilan yang diperlukan untuk memecahkan masalah integral tentu dengan percaya diri dan efisien.

Ringkasan FAQ

Apa itu integral tentu?

Integral tentu adalah proses penjumlahan tak hingga dari luas persegi panjang yang sangat kecil untuk menentukan luas suatu daerah di bawah kurva.

Apa saja metode umum untuk mengerjakan integral tentu?

Metode umum termasuk metode Riemann, metode Trapezoidal, dan metode Simpson.

Bagaimana integral tentu digunakan dalam kehidupan nyata?

Integral tentu digunakan untuk menghitung luas, volume, pusat massa, dan banyak besaran lainnya yang penting dalam fisika, teknik, dan bidang lainnya.