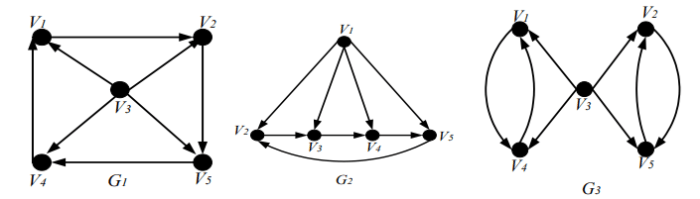
Graf sederhana merupakan struktur data yang ampuh yang digunakan untuk memodelkan hubungan antar objek dalam berbagai bidang. Graf sederhana terdiri dari sekumpulan simpul dan sekumpulan tepi yang menghubungkan simpul-simpul tersebut. Artikel ini akan menyajikan contoh graf sederhana dengan 5 simpul, membahas cara menggambar, merepresentasikan secara matematis, dan mengaplikasikannya dalam kehidupan nyata.
Dalam graf sederhana dengan 5 simpul, setiap simpul dapat dihubungkan ke simpul lain dengan maksimal satu tepi. Struktur ini memungkinkan kita untuk merepresentasikan hubungan antar objek dengan cara yang jelas dan mudah dipahami.
Pengertian Graf Sederhana
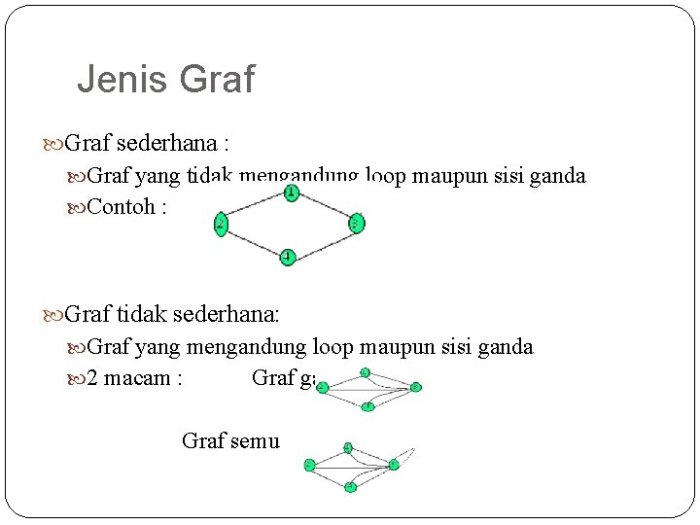
Graf sederhana adalah sebuah struktur data yang merepresentasikan relasi antara sejumlah objek, yang disebut simpul. Dalam graf sederhana, setiap pasangan simpul dapat terhubung oleh tepat satu sisi. Sisi-sisi ini dapat berarah atau tidak berarah.
Contoh Graf Sederhana dengan 5 Simpul
Contoh graf sederhana dengan 5 simpul dapat digambarkan sebagai berikut:
- Simpul: A, B, C, D, E
- Sisi: AB, AC, AD, AE, BC, BD, CE
Cara Menggambar Graf Sederhana
Menggambar graf sederhana merupakan langkah penting dalam memahami dan merepresentasikan hubungan antar simpul dalam sebuah jaringan. Berikut adalah langkah-langkah untuk menggambar graf sederhana dengan 5 simpul:
Mengidentifikasi Simpul
Mulailah dengan mengidentifikasi simpul-simpul dalam graf. Simpul biasanya diwakili oleh titik atau lingkaran dan diberi label dengan huruf atau angka. Dalam contoh ini, kita akan menggunakan simpul A, B, C, D, dan E.
Menggambar Simpul
Gambarkan simpul-simpul pada selembar kertas atau di perangkat lunak pengolah grafik. Pastikan simpul-simpul tersebut terpisah dan mudah dikenali.
Mengidentifikasi Tepi
Tepi adalah garis yang menghubungkan dua simpul. Identifikasi tepi-tepi dalam graf dan tentukan simpul mana yang terhubung oleh setiap tepi.
Menggambar Tepi
Gambarkan tepi-tepi yang menghubungkan simpul-simpul yang sesuai. Tepi dapat berupa garis lurus atau melengkung. Jika tepi berarah, tandai dengan tanda panah.
Contoh
Sebagai contoh, perhatikan graf sederhana dengan 5 simpul berikut:
- Simpul: A, B, C, D, E
- Tepi: AB, AC, BC, CD, CE
Untuk menggambar graf ini, ikuti langkah-langkah di atas:
- Gambar simpul A, B, C, D, dan E pada selembar kertas.
- Hubungkan simpul A ke B dengan garis.
- Hubungkan simpul A ke C dengan garis.
- Hubungkan simpul B ke C dengan garis.
- Hubungkan simpul C ke D dengan garis.
- Hubungkan simpul C ke E dengan garis.
Representasi Matematis Graf Sederhana
Graf sederhana dapat direpresentasikan secara matematis menggunakan matriks adjacency. Matriks adjacency adalah matriks persegi di mana elemen-elemennya mewakili hubungan antar simpul dalam graf.
Matriks Adjacency
Matriks adjacency A berukuran n x n, di mana n adalah jumlah simpul dalam graf. Elemen a ij dari matriks A menyatakan hubungan antara simpul i dan j. Jika ada edge yang menghubungkan simpul i dan j, maka a ij = 1. Jika tidak ada edge yang menghubungkan simpul i dan j, maka a ij = 0.Berikut
adalah contoh matriks adjacency untuk graf sederhana dengan 5 simpul:
| v1 | v2 | v3 | v4 | v5 | |
| v1 | 0 | 1 | 0 | 0 | 1 |
| v2 | 1 | 0 | 1 | 0 | 0 |
| v3 | 0 | 1 | 0 | 1 | 0 |
| v4 | 0 | 0 | 1 | 0 | 1 |
| v5 | 1 | 0 | 0 | 1 | 0 |
Matriks adjacency dapat digunakan untuk mewakili berbagai sifat graf, seperti derajat simpul, jarak antar simpul, dan jalur terpendek antar simpul.
Aplikasi Graf Sederhana
Graf sederhana memiliki aplikasi luas dalam kehidupan nyata, mewakili berbagai hubungan dan struktur data. Berikut beberapa contoh penggunaannya:
Bidang Sosial
- Jaringan sosial: Graf mewakili pengguna sebagai simpul dan hubungan pertemanan sebagai sisi, memungkinkan analisis komunitas dan penyebaran informasi.
- Peta jaringan: Graf digunakan untuk memodelkan hubungan antara individu dalam suatu kelompok, membantu mengidentifikasi pemimpin opini dan pengaruh sosial.
Bidang Komputer
- Struktur data: Graf digunakan untuk menyimpan dan mengelola data yang saling berhubungan, seperti daftar kedekatan dan daftar insiden.
- Algoritma: Graf digunakan dalam berbagai algoritma, seperti pencarian jalur terpendek (algoritma Dijkstra), pencocokan pola (algoritma Knuth-Morris-Pratt), dan penyortiran topologi.
Bidang Teknik
- Jaringan komputer: Graf digunakan untuk memodelkan topologi jaringan, membantu mengoptimalkan rute dan meningkatkan kinerja.
- Sistem transportasi: Graf digunakan untuk memodelkan rute transportasi, memungkinkan perencanaan rute yang efisien dan pengoptimalan lalu lintas.
Contoh Graf Sederhana dengan 5 Simpul
Graf sederhana adalah graf yang tidak memiliki tepi ganda atau simpul ganda. Berikut ini adalah contoh graf sederhana dengan 5 simpul:
Tabel Contoh Graf Sederhana dengan 5 Simpul
| Simpul | Tepi ||—|—|| A | AB, AC || B | BA, BC || C | CA, CD || D | CD, DE || E | DE |
Cara Membuat Graf Sederhana dengan 5 Simpul
Graf sederhana merupakan representasi matematis dari himpunan titik-titik (disebut simpul) yang dihubungkan oleh garis-garis (disebut sisi). Berikut adalah prosedur langkah demi langkah untuk membuat graf sederhana dengan 5 simpul:
Langkah-langkah Membuat Graf Sederhana dengan 5 Simpul
- Tentukan himpunan simpul. Dalam hal ini, kita akan menggunakan A, B, C, D, E.
- Buatlah daftar sisi yang menghubungkan simpul-simpul tersebut. Misalnya, (A, B), (A, C), (B, C), (C, D), (D, E).
- Gambarkan simpul-simpul sebagai titik-titik pada bidang. Misalnya, A dapat digambarkan sebagai titik di sudut kiri atas, B di sudut kanan atas, C di sudut kanan bawah, D di sudut kiri bawah, dan E di tengah.
- Hubungkan simpul-simpul yang memiliki sisi dengan garis-garis. Misalnya, gambar garis dari A ke B, A ke C, B ke C, C ke D, dan D ke E.
- Graf sederhana dengan 5 simpul telah selesai dibuat.
Karakteristik Graf Sederhana dengan 5 Simpul
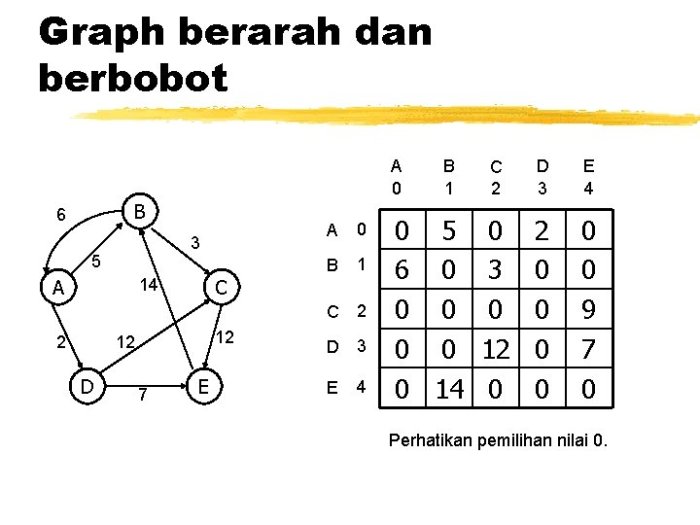
Graf sederhana dengan 5 simpul adalah struktur matematika yang mewakili hubungan antar objek. Graf tersebut memiliki beberapa karakteristik khusus yang membedakannya dari jenis graf lainnya.
Graf sederhana dengan 5 simpul terdiri dari 5 titik (simpul) yang dihubungkan oleh garis (sisi). Setiap sisi mewakili hubungan antara dua simpul. Graf tersebut tidak memiliki loop (sisi yang menghubungkan simpul ke dirinya sendiri) atau sisi ganda (sisi yang menghubungkan dua simpul yang sama lebih dari satu kali).
Sifat Unik Graf Sederhana dengan 5 Simpul
- Jumlah sisi maksimum adalah 10.
- Derajat maksimum setiap simpul adalah 4.
- Graf tersebut dapat diwarnai dengan 3 warna.
- Graf tersebut dapat dibagi menjadi 2 komponen yang terhubung.
Representasi Visual Graf Sederhana dengan 5 Simpul

Graf sederhana dengan 5 simpul dapat direpresentasikan secara visual sebagai diagram yang menghubungkan simpul-simpul dengan garis atau tepi. Representasi ini memberikan gambaran yang jelas tentang hubungan antar simpul dalam graf.
Ilustrasi Visual
Berikut adalah ilustrasi visual dari graf sederhana dengan 5 simpul:
- Simpul A terhubung ke simpul B dengan sebuah tepi.
- Simpul B terhubung ke simpul C dan D dengan dua tepi.
- Simpul C terhubung ke simpul D dan E dengan dua tepi.
- Simpul D terhubung ke simpul E dengan sebuah tepi.
- Simpul E terhubung ke simpul A dengan sebuah tepi.
Akhir Kata

Graf sederhana dengan 5 simpul merupakan contoh penting dari struktur data graf. Mereka memiliki berbagai aplikasi dalam kehidupan nyata, seperti pemodelan jaringan sosial, jaringan transportasi, dan sistem komputer. Memahami cara kerja graf sederhana sangat penting untuk memanfaatkan potensi mereka secara maksimal.
Pertanyaan dan Jawaban
Apa saja karakteristik unik dari graf sederhana dengan 5 simpul?
Graf sederhana dengan 5 simpul memiliki karakteristik khusus, seperti derajat maksimal setiap simpul adalah 4 dan jumlah tepi maksimal adalah 10.
Bagaimana cara merepresentasikan graf sederhana dengan 5 simpul secara matematis?
Graf sederhana dengan 5 simpul dapat direpresentasikan menggunakan matriks adjacency, di mana setiap elemen mewakili keberadaan tepi antara dua simpul.
Apa saja aplikasi dari graf sederhana dengan 5 simpul?
Graf sederhana dengan 5 simpul dapat digunakan untuk memodelkan jaringan sosial kecil, sistem transportasi dengan 5 pemberhentian, atau jaringan komputer dengan 5 perangkat.