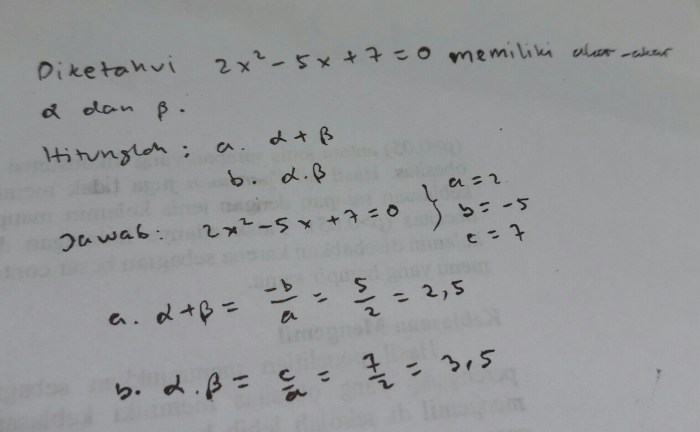Akar kuadrat merupakan konsep matematika penting yang banyak diaplikasikan dalam berbagai bidang. Memahami akar kuadrat sangat penting untuk memecahkan masalah yang melibatkan geometri, fisika, dan keuangan.
Dalam artikel ini, kita akan mengeksplorasi konsep akar kuadrat, metode untuk mencari akar kuadrat, dan contoh soal beserta jawabannya. Kita juga akan membahas beberapa tips dan trik untuk menyelesaikan soal akar kuadrat dengan lebih cepat dan akurat.
Pengertian Akar Kuadrat
Akar kuadrat dari suatu bilangan adalah bilangan yang, ketika dikuadratkan, menghasilkan bilangan aslinya. Akar kuadrat dari bilangan a dinyatakan sebagai √a, di mana a adalah bilangan yang diakar.
Rumus Akar Kuadrat
Rumus umum untuk akar kuadrat dari bilangan a adalah:
√a = ±√a
Tanda ± menunjukkan bahwa akar kuadrat dari bilangan positif memiliki dua solusi, satu positif dan satu negatif. Misalnya, akar kuadrat dari 4 adalah 2 dan -2.
Contoh Akar Kuadrat
- √4 = 2 karena 2² = 4
- √9 = 3 karena 3² = 9
- √16 = 4 karena 4² = 16
- √25 = 5 karena 5² = 25
- √100 = 10 karena 10² = 100
Cara Mencari Akar Kuadrat
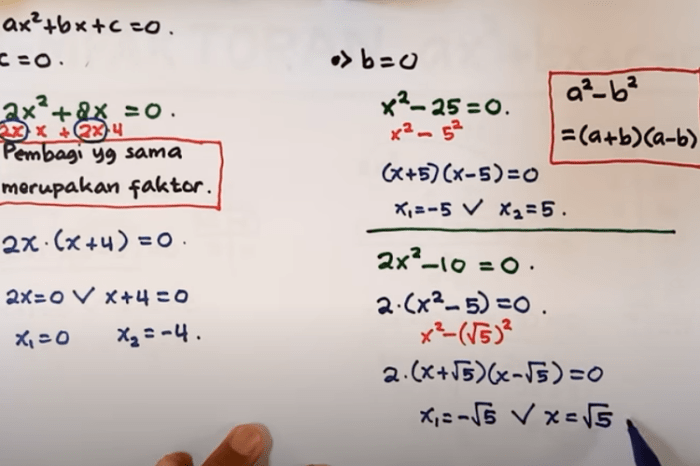
Akar kuadrat dari sebuah bilangan adalah bilangan yang jika dikuadratkan akan menghasilkan bilangan awal. Ada beberapa metode untuk mencari akar kuadrat, baik secara manual maupun menggunakan alat bantu.
Metode Pembagian Panjang
Metode pembagian panjang digunakan untuk mencari akar kuadrat bilangan bulat yang tidak sempurna. Langkah-langkahnya sebagai berikut:
- Pisahkan bilangan menjadi pasangan angka, dimulai dari titik desimal.
- Cari bilangan terbesar yang kuadratnya kurang dari atau sama dengan pasangan angka pertama.
- Kurangkan kuadrat bilangan tersebut dari pasangan angka pertama.
- Turunkan pasangan angka berikutnya dan gabungkan dengan sisa pembagian sebelumnya.
- Ulangi langkah 2-4 hingga tidak ada lagi pasangan angka.
Menggunakan Kalkulator
Kalkulator dapat digunakan untuk mencari akar kuadrat dengan mudah. Sebagian besar kalkulator memiliki tombol khusus untuk menghitung akar kuadrat, yang biasanya diberi label “√”.
Metode Newton-Raphson
Metode Newton-Raphson adalah metode iteratif yang dapat digunakan untuk mencari akar kuadrat bilangan real. Algoritmanya sebagai berikut:
$$x_n+1 = x_n
- \fracx_n^2
- a2x_n$$
di mana:
- $a$ adalah bilangan yang akar kuadratnya ingin dicari
- $x_n$ adalah perkiraan akar kuadrat saat ini
- $x_n+1$ adalah perkiraan akar kuadrat berikutnya
Aplikasi Akar Kuadrat

Akar kuadrat merupakan operasi matematika yang banyak digunakan dalam berbagai bidang. Konsep ini penting untuk menyelesaikan masalah yang melibatkan perhitungan jarak, luas, dan volume dalam geometri, dinamika dalam fisika, serta investasi dalam keuangan.
Geometri
- Menghitung panjang sisi segitiga siku-siku menggunakan Teorema Pythagoras:
Panjang sisi miring = akar kuadrat(Panjang sisi pertama2 + Panjang sisi kedua2) - Mencari diameter lingkaran dari jari-jarinya:
Diameter = 2 x akar kuadrat(Jari-jari)
Fisika
- Menghitung kecepatan benda yang jatuh bebas:
Kecepatan = akar kuadrat(2 x Gravitasi x Tinggi jatuh) - Menentukan momentum benda:
Momentum = akar kuadrat(2 x Massa x Energi kinetik)
Keuangan
- Menghitung nilai investasi setelah jangka waktu tertentu menggunakan rumus bunga majemuk:
Nilai investasi = Nilai awal x (1 + Suku bunga)Waktu - Menentukan tingkat pengembalian tahunan dari nilai investasi yang diketahui:
Tingkat pengembalian tahunan = ((Nilai akhir / Nilai awal)1 / Waktu
– 1) x 100%
Contoh Soal dan Jawaban Akar Kuadrat

Akar kuadrat adalah operasi matematika yang mencari angka yang, ketika dikalikan dengan dirinya sendiri, menghasilkan angka asli yang diberikan. Dalam istilah aljabar, akar kuadrat dari x, ditulis sebagai √x, adalah angka y yang memenuhi persamaan y² = x.
Contoh Soal
Berikut adalah tabel berisi contoh soal akar kuadrat dengan tingkat kesulitan yang bervariasi:
| Soal | Metode | Langkah-langkah | Jawaban |
|---|---|---|---|
| √16 | Faktorisasi prima | 16 = 2 × 2 × 2 × 2 | 4 |
| √81 | Menggunakan tabel perkalian | 9 × 9 = 81 | 9 |
| √121 | Pembagian berulang | 121 ÷ 11 = 11, sisa 0 | 11 |
| √256 | Pengurangan sempurna | 256 = 16 × 16 | 16 |
| √1000 | Perkiraan | 1000 berada di antara 30² dan 40², jadi √1000 ≈ 32 | ≈ 32 |
Tips dan Trik

Berikut adalah beberapa tips dan trik untuk menyelesaikan soal akar kuadrat dengan lebih cepat dan akurat:
Perkiraan
Untuk akar kuadrat yang tidak sempurna, mulailah dengan memperkirakan akarnya. Misalnya, untuk mencari akar kuadrat dari 25, perkiraan terdekat adalah 5.
Metode Pembagian
Gunakan metode pembagian untuk mencari akar kuadrat dari bilangan besar. Metode ini membagi bilangan menjadi beberapa kelompok angka dan kemudian melakukan pembagian secara bertahap.
Identitas Akar Kuadrat
Gunakan identitas akar kuadrat berikut untuk menyederhanakan soal:
- (a + b)² = a² + 2ab + b²
- (a
– b)² = a²
– 2ab + b²- √(ab) = √a
– √b
Hindari Kesalahan Umum
Hindari kesalahan umum berikut saat menyelesaikan soal akar kuadrat:
- Mencampur akar kuadrat dengan pangkat dua.
- Lupa menulis simbol akar kuadrat pada jawaban.
- Menyederhanakan akar kuadrat yang tidak dapat disederhanakan lebih lanjut.
Ringkasan Terakhir
Akar kuadrat merupakan alat matematika yang ampuh yang memiliki aplikasi luas dalam kehidupan nyata. Dengan memahami konsep dan teknik yang diuraikan dalam artikel ini, individu dapat dengan percaya diri menyelesaikan soal akar kuadrat dan menerapkan pengetahuan mereka untuk memecahkan masalah di berbagai bidang.
Bagian Pertanyaan Umum (FAQ)
Apa itu akar kuadrat?
Akar kuadrat suatu bilangan adalah bilangan yang jika dikalikan dengan dirinya sendiri menghasilkan bilangan asli tersebut.
Bagaimana cara mencari akar kuadrat?
Ada beberapa metode untuk mencari akar kuadrat, termasuk metode pembagian panjang, kalkulator, dan metode Newton-Raphson.
Di bidang apa saja akar kuadrat digunakan?
Akar kuadrat digunakan dalam berbagai bidang, seperti geometri, fisika, dan keuangan.