Aturan cosinus, sebuah teorema penting dalam trigonometri, memberikan metode yang andal untuk menentukan sisi atau sudut segitiga manapun, asalkan dua sisi dan satu sudut yang disertakan diketahui. Dengan pemahaman yang jelas tentang konsep ini dan langkah-langkah yang terlibat dalam penggunaannya, kita dapat mengatasi berbagai masalah trigonometri dengan efisiensi dan akurasi.

Dalam artikel ini, kita akan mengeksplorasi aturan cosinus secara menyeluruh, mulai dari rumus hingga contoh soal dan aplikasinya dalam kehidupan nyata. Dengan pendekatan bertahap, kita akan mengungkap misteri teorema yang sangat berguna ini dan membuka jalan untuk memecahkan masalah trigonometri yang kompleks.

Pengertian Aturan Cosinus

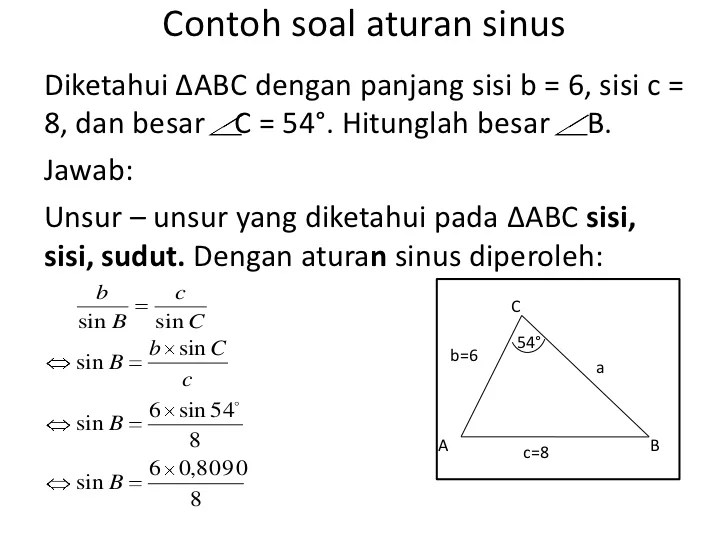
Aturan cosinus adalah teorema dalam trigonometri yang digunakan untuk menghitung panjang sisi sebuah segitiga ketika diketahui dua sisi dan sudut di antara keduanya.

Aturan ini menyatakan bahwa dalam segitiga ABC, di mana c adalah sisi berlawanan sudut C, a dan b adalah sisi-sisi yang berdekatan dengan sudut C, dan θ adalah besar sudut C, maka panjang sisi c dapat dihitung dengan rumus:

c² = a² + b²

2ab cos(θ)

Contoh Penerapan Aturan Cosinus

• Menghitung panjang sisi miring segitiga siku-siku.
• Menghitung panjang sisi sebuah segitiga tidak siku-siku.
• Menentukan posisi suatu titik dalam bidang koordinat menggunakan segitiga.

Rumus Aturan Cosinus

Dalam trigonometri, aturan cosinus adalah rumus yang menghubungkan panjang sisi segitiga dengan sudut di antara sisi tersebut. Rumus ini digunakan untuk menghitung panjang sisi atau sudut segitiga ketika dua sisi dan sudut di antara keduanya diketahui.

Rumus Aturan Cosinus

Rumus aturan cosinus menyatakan bahwa untuk segitiga dengan sisi a , b , dan c , dan sudut C di seberang sisi c , berlaku:

c² = a² + b²

2ab cos(C)

Di mana:

• c adalah panjang sisi di seberang sudut C.
• a dan b adalah panjang kedua sisi lainnya.
• C adalah sudut di seberang sisi c.

Langkah-langkah Menggunakan Aturan Cosinus

Aturan cosinus adalah teorema yang digunakan untuk mencari panjang sisi segitiga ketika diketahui panjang dua sisi dan besar salah satu sudutnya.

Langkah-langkah Menggunakan Aturan Cosinus

1. Identifikasi dua sisi yang diketahui dan sudut yang diketahui. Beri label sisi-sisi tersebut sebagai a, b, dan c, dengan c sebagai sisi yang berlawanan dengan sudut yang diketahui.
2. Substitusikan nilai-nilai yang diketahui ke dalam rumus aturan cosinus. Rumusnya adalah: c² = a² + b²
   

   2ab cos(C), di mana C adalah besar sudut yang diketahui.

3. Selesaikan persamaan untuk mencari panjang sisi c. Kuadratkan kedua sisi persamaan dan selesaikan untuk c.

Contoh Soal dan Penyelesaian

Aturan cosinus adalah teorema trigonometri yang digunakan untuk mencari sisi atau sudut segitiga manapun, jika diketahui dua sisi dan sudut yang diapit oleh kedua sisi tersebut.

Berikut adalah beberapa contoh soal aturan cosinus:

Soal 1

Sebuah segitiga memiliki dua sisi yang panjangnya 5 cm dan 7 cm. Sudut yang diapit oleh kedua sisi tersebut adalah 60 derajat. Tentukan panjang sisi ketiga segitiga tersebut.

Penyelesaian:

* Diketahui: a = 5 cm, b = 7 cm, C = 60 derajat

Gunakan rumus aturan cosinus

c² = a² + b²2ab cos C

• Substitusikan nilai yang diketahui

  c² = 5² + 7²

• 2(5)(7) cos 60

Hitung nilai c²

c² = 25 + 49

• 70(0,5) = 54

Tentukan panjang sisi ketiga

c = √54 = 7,35 cm

Soal 2

Sebuah segitiga memiliki dua sisi yang panjangnya 10 cm dan 15 cm. Sudut yang diapit oleh kedua sisi tersebut adalah 120 derajat. Tentukan besar sudut yang berhadapan dengan sisi terpanjang.

Penyelesaian:

* Diketahui: a = 10 cm, b = 15 cm, C = 120 derajat

Gunakan rumus aturan cosinus

cos C = (a² + b²c²) / 2ab

• Substitusikan nilai yang diketahui

  cos 120 = (10² + 15²

• c²) / 2(10)(15)

Hitung nilai cos 120

cos 120 = (100 + 225

• c²) / 300 =
• 0,5

Tentukan besar sudut yang berhadapan dengan sisi terpanjang

B = arccos(-0,5) = 120 derajat

Soal 3

Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 100 km. Kapal tersebut kemudian berlayar ke pelabuhan C sejauh 150 km dengan arah 60 derajat dari arah pelayaran pertama.

Tentukan jarak antara pelabuhan A dan C.

Penyelesaian:

* Diketahui: a = 100 km, b = 150 km, C = 60 derajat

Gunakan rumus aturan cosinus

c² = a² + b²2ab cos C

• Substitusikan nilai yang diketahui

  c² = 100² + 150²

• 2(100)(150) cos 60

Hitung nilai c²

c² = 10000 + 22500

• 30000(0,5) = 16250

Tentukan jarak antara pelabuhan A dan C

c = √16250 = 127,5 km

Variasi Soal Aturan Cosinus

Aturan cosinus adalah rumus yang digunakan untuk mencari panjang sisi suatu segitiga jika diketahui panjang dua sisi dan besar sudut yang diapit oleh kedua sisi tersebut.

Variasi soal aturan cosinus dapat berupa:

• Mencari panjang sisi segitiga jika diketahui dua sisi dan sudut yang tidak diapit oleh kedua sisi tersebut.
• Mencari besar sudut segitiga jika diketahui panjang ketiga sisinya.
• Mencari luas segitiga jika diketahui panjang ketiga sisinya.

Tips Menyelesaikan Variasi Soal Aturan Cosinus

Untuk menyelesaikan variasi soal aturan cosinus, terdapat beberapa tips yang dapat diterapkan:

1. Gambarlah segitiga dan beri label pada sisi dan sudut yang diketahui.
2. Pilih rumus aturan cosinus yang sesuai dengan variasi soal yang dikerjakan.
3. Substitusikan nilai yang diketahui ke dalam rumus dan selesaikan untuk variabel yang tidak diketahui.
4. Periksa kembali jawaban yang diperoleh.

Aplikasi Aturan Cosinus dalam Kehidupan Nyata

Aturan cosinus adalah teorema yang digunakan untuk mencari panjang sisi segitiga jika diketahui panjang kedua sisi lainnya dan besar salah satu sudutnya. Aturan ini banyak diterapkan dalam berbagai bidang kehidupan nyata, seperti navigasi, survei, dan teknik.

Survei Tanah

Dalam survei tanah, aturan cosinus digunakan untuk menentukan jarak antara dua titik yang tidak dapat diukur secara langsung. Misalnya, seorang surveyor mungkin perlu menentukan jarak antara dua pohon yang terhalang oleh sungai. Dengan mengukur panjang dua sisi segitiga yang dibentuk oleh pohon dan sungai, serta sudut yang terbentuk di antara kedua sisi tersebut, surveyor dapat menggunakan aturan cosinus untuk menghitung jarak yang tidak dapat diukur.

Latihan Soal Aturan Cosinus

Untuk mengasah pemahaman tentang aturan cosinus, berikut adalah beberapa latihan soal beserta jawaban atau petunjuk penyelesaiannya.

Soal 1

Diketahui segitiga ABC dengan panjang sisi AB = 6 cm, BC = 8 cm, dan sudut C = 60°. Tentukan panjang sisi AC.

Jawaban: 10 cm

Soal 2

Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B yang berjarak 100 km. Kapal tersebut berlayar dengan sudut 30° terhadap garis lurus AB. Berapa jarak kapal dari pelabuhan A setelah berlayar selama 2 jam dengan kecepatan 50 km/jam?

Petunjuk: Gunakan aturan cosinus untuk mencari panjang segmen AB dan kemudian kalikan dengan waktu tempuh untuk mencari jarak yang ditempuh.

Soal 3

Diketahui segitiga PQR dengan panjang sisi PQ = 12 cm, QR = 15 cm, dan PR = 18 cm. Hitunglah besar sudut Q.

Petunjuk: Gunakan aturan cosinus untuk mencari nilai cosinus sudut Q dan kemudian cari nilai sudut Q menggunakan invers cosinus.

Soal 4

Sebuah lapangan berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya 8 m dan 6 m. Sebuah pohon ditanam di dalam lapangan dengan jarak 5 m dari salah satu sisi siku-siku dan 4 m dari sisi miring. Hitunglah jarak pohon dari sisi siku-siku yang lain.

Petunjuk: Bagilah lapangan menjadi dua segitiga siku-siku dan gunakan aturan cosinus untuk mencari jarak yang ditanyakan.

Kesimpulan

Aturan cosinus terbukti menjadi alat yang ampuh untuk memecahkan masalah trigonometri yang melibatkan segitiga. Dengan memahami rumus, langkah-langkah, dan variasinya, kita dapat memperoleh solusi yang akurat untuk berbagai skenario. Aplikasi praktisnya dalam bidang teknik, survei, dan navigasi menyoroti nilai teorema ini dalam kehidupan nyata.

Menguasai aturan cosinus membuka gerbang ke pemahaman yang lebih dalam tentang trigonometri dan aplikasi praktisnya di berbagai bidang.

Pertanyaan Umum (FAQ)

Apa itu aturan cosinus?

Aturan cosinus adalah rumus yang digunakan untuk mencari panjang sisi atau besar sudut segitiga jika diketahui dua sisi dan sudut yang diapit oleh kedua sisi tersebut.

Bagaimana cara menggunakan aturan cosinus?

Aturan cosinus dapat digunakan dengan mengikuti langkah-langkah berikut:

1. Identifikasi dua sisi yang diketahui dan sudut yang diapit oleh kedua sisi tersebut.
2. Gunakan rumus aturan cosinus untuk mencari sisi atau sudut yang tidak diketahui.

Apa saja variasi soal aturan cosinus?

Variasi soal aturan cosinus meliputi: