Dilatasi, salah satu transformasi geometri yang fundamental, memainkan peran penting dalam memahami hubungan spasial dan aplikasi praktisnya dalam berbagai bidang. Artikel ini menyajikan panduan komprehensif tentang konsep dilatasi, dilengkapi dengan contoh soal yang disusun secara sistematis untuk membantu siswa kelas 9 menguasai topik ini.

Dilatasi adalah transformasi yang memperbesar atau memperkecil suatu bangun dengan faktor skala tertentu. Konsep ini memiliki aplikasi yang luas dalam bidang teknik, arsitektur, dan desain, sehingga pemahaman yang mendalam sangat penting untuk siswa yang ingin mendalami bidang-bidang tersebut.

Definisi Dilatasi

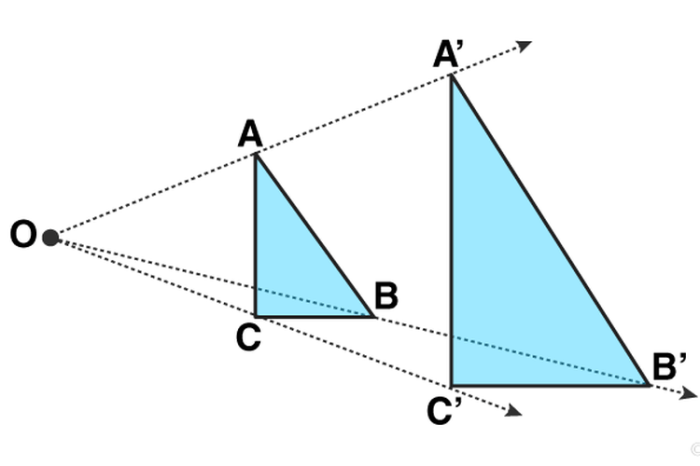
Dilatasi merupakan transformasi geometri yang memperbesar atau memperkecil suatu bangun geometri dengan faktor tertentu tanpa mengubah bentuknya. Faktor penggandaan atau pengecilan ini dikenal sebagai faktor skala.

Secara visual, dilatasi dapat dibayangkan sebagai memperbesar atau memperkecil suatu bangun dengan mempertahankan titik pusatnya tetap.

Faktor Skala

Faktor skala dalam dilatasi adalah bilangan positif yang menentukan seberapa besar atau kecil suatu bangun akan diperbesar atau diperkecil. Faktor skala lebih besar dari 1 akan memperbesar bangun, sedangkan faktor skala kurang dari 1 akan memperkecil bangun.

Titik Pusat

Titik pusat dalam dilatasi adalah titik tetap yang tidak berubah posisinya saat bangun diubah ukurannya. Semua titik lain dalam bangun akan diperbesar atau diperkecil relatif terhadap titik pusat.

Rumus Dilatasi

Dilatasi adalah transformasi geometri yang memperbesar atau memperkecil suatu bangun dengan faktor tertentu. Rumus dilatasi digunakan untuk menentukan koordinat titik setelah dilatasi.

Pusat Dilatasi dan Faktor Skala

*

• *Pusat dilatasi adalah titik tetap yang tidak berubah posisinya selama dilatasi.
• *Faktor skala adalah bilangan positif yang menentukan perbesaran atau pengecilan bangun.

Rumus Dilatasi

Rumus dilatasi untuk titik (x, y) dengan pusat dilatasi (h, k) dan faktor skala k adalah:“`x’ = k(x

h) + h

y’ = k(y

k) + k

“`di mana:* (x’, y’) adalah koordinat titik setelah dilatasi

• (x, y) adalah koordinat titik sebelum dilatasi
• (h, k) adalah koordinat pusat dilatasi
• k adalah faktor skala

Tabel Rumus Dilatasi

Berikut tabel rumus dilatasi untuk berbagai faktor skala:| Faktor Skala | Rumus ||—|—|| k = 1 | Tidak ada perubahan || k > 1 | Perbesaran || k < 1 | Pengecilan | | k = 0 | Titik runtuh ke pusat dilatasi |

Contoh Soal Dilatasi

Dilatasi adalah transformasi geometri yang memperbesar atau memperkecil suatu bangun dengan faktor tertentu.

Contoh Soal Dilatasi Titik

Dilatasi titik P(2, 3) dengan faktor skala 2 menghasilkan titik P'(x, y).

Tentukan nilai x dan y.

Contoh Soal Dilatasi Garis

Dilatasi garis 2x + 3y = 6 dengan faktor skala 1/2 menghasilkan garis baru.

Tuliskan persamaan garis baru.

Contoh Soal Dilatasi Bangun Datar

Sebuah persegi panjang dengan panjang 5 cm dan lebar 3 cm didilatasi dengan faktor skala 3.

Tentukan luas persegi panjang setelah dilatasi.

Langkah-langkah Menyelesaikan Soal Dilatasi

Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun tanpa mengubah bentuknya. Berikut adalah langkah-langkah untuk menyelesaikan soal dilatasi:

Identifikasi Pusat Dilatasi

Pusat dilatasi adalah titik yang menjadi pusat pembesaran atau pengecilan. Pusat dilatasi biasanya diberikan dalam soal.

Tentukan Faktor Skala

Faktor skala adalah angka yang menunjukkan seberapa besar suatu bangun diperbesar atau diperkecil. Faktor skala selalu positif, dan biasanya ditulis dalam bentuk k. Jika k > 1, bangun akan diperbesar. Jika k< 1, bangun akan diperkecil.

Gunakan Rumus Dilatasi

Rumus dilatasi digunakan untuk mencari koordinat titik-titik pada bangun yang didilatasi. Rumusnya adalah:

P'(x’, y’) = (k

• x, k
• y)

di mana:

• P(x, y) adalah koordinat titik pada bangun asli
• P'(x’, y’) adalah koordinat titik pada bangun yang didilatasi
• k adalah faktor skala

Contoh Ilustrasi

Misalkan kita memiliki segitiga dengan koordinat titik A(2, 3), B(4, 5), dan C(6, 3). Segitiga tersebut didilatasi dengan pusat dilatasi di titik (0, 0) dan faktor skala k = 2.

Langkah-langkah penyelesaian:

1. Pusat dilatasi: (0, 0)
2. Faktor skala: k = 2
3. Koordinat titik-titik pada segitiga yang didilatasi:
• A'(2
  – 2, 3
  – 2) = (4, 6)
• B'(4
  – 2, 5
  – 2) = (8, 10)
• C'(6
  – 2, 3
  – 2) = (12, 6)

Aplikasi Dilatasi

Dilatasi memiliki berbagai aplikasi dalam kehidupan nyata, seperti:

Pengecilan dan Pembesaran Gambar

Dilatasi digunakan untuk memperbesar atau memperkecil gambar tanpa mengubah bentuknya. Dalam fotografi, misalnya, dilatasi digunakan untuk memperbesar bagian tertentu dari gambar atau untuk memperkecil gambar untuk keperluan tertentu.

Bidang Teknik, Arsitektur, dan Desain

Dalam teknik, dilatasi digunakan untuk mendesain struktur yang harus menahan beban yang berat. Dalam arsitektur, dilatasi digunakan untuk membuat desain bangunan yang proporsional dan estetis. Dalam desain, dilatasi digunakan untuk membuat pola dan bentuk yang unik.

Penutup

Dengan menguasai konsep dan langkah-langkah penyelesaian dilatasi, siswa kelas 9 akan memiliki dasar yang kuat untuk menjelajahi transformasi geometri yang lebih kompleks. Pemahaman yang komprehensif ini akan membuka pintu ke aplikasi praktis dilatasi dalam berbagai bidang, memberdayakan mereka untuk memecahkan masalah dunia nyata secara efektif.

Pertanyaan Umum yang Sering Muncul

Apa itu faktor skala dalam dilatasi?

Faktor skala adalah bilangan yang menentukan seberapa besar suatu bangun diperbesar atau diperkecil. Faktor skala lebih besar dari 1 menghasilkan pembesaran, sedangkan faktor skala kurang dari 1 menghasilkan pengecilan.

Bagaimana cara mengidentifikasi pusat dilatasi?

Pusat dilatasi adalah titik tetap yang menjadi pusat pembesaran atau pengecilan. Dalam soal dilatasi, pusat dilatasi biasanya diberikan atau dapat ditentukan dari koordinat titik-titik yang mengalami transformasi.

Apa saja aplikasi praktis dilatasi?

Dilatasi memiliki banyak aplikasi dalam kehidupan nyata, seperti pembesaran gambar dalam fotografi, perencanaan skala dalam arsitektur, dan desain produk. Dalam teknik, dilatasi digunakan untuk membuat model skala dari struktur dan mesin yang lebih besar.