Dalam matematika, fungsi invers memainkan peran penting dalam memecahkan berbagai masalah. Fungsi ini merupakan konsep dasar aljabar yang sering muncul pada jenjang pendidikan menengah atas, khususnya kelas 10. Untuk memahami konsep ini secara mendalam, artikel ini akan mengulas pengertian, sifat, cara menentukan, aplikasi, serta contoh soal fungsi invers kelas 10 beserta pembahasannya.
Artikel ini disusun dengan gaya ilmiah yang objektif dan memberikan penjelasan yang jelas dan komprehensif. Selain itu, artikel ini juga dilengkapi dengan daftar FAQ untuk menjawab pertanyaan umum yang sering diajukan terkait topik ini.
Pengertian Fungsi Invers
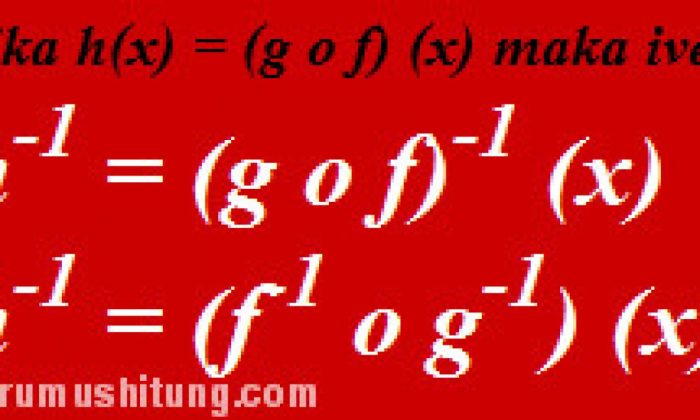
Dalam matematika, fungsi invers adalah fungsi yang membatalkan fungsi lainnya. Artinya, jika fungsi f diterapkan pada suatu bilangan x dan kemudian fungsinya diinvers, maka hasilnya adalah x.
Secara formal, fungsi invers dari fungsi f, dilambangkan dengan f -1 , adalah fungsi yang memenuhi:
f(f -1 (x)) = x untuk semua x di domain f -1
f -1 (f(x)) = x untuk semua x di domain f
Contoh Fungsi Invers
Salah satu contoh sederhana fungsi invers adalah fungsi kuadrat f(x) = x 2 . Fungsi inversnya adalah f -1 (x) = √x.
Jika f(x) = x 2 diterapkan pada bilangan 4, hasilnya adalah 16. Jika kemudian fungsinya diinvers, f -1 (16) = √16 = 4, sehingga menghasilkan bilangan asli.
Sifat-Sifat Fungsi Invers
Fungsi invers, yang dilambangkan dengan f^-1(x), memiliki sifat-sifat khusus yang membedakannya dari fungsi aslinya. Sifat-sifat ini meliputi:
Sifat-Sifat Umum Fungsi Invers
- Domain fungsi invers adalah range fungsi aslinya.
- Range fungsi invers adalah domain fungsi aslinya.
- Grafik fungsi invers adalah cerminan grafik fungsi aslinya terhadap garis y = x.
Contoh Fungsi Invers
- Fungsi f(x) = x^2 memiliki fungsi invers f^-1(x) = ±√x.
- Fungsi f(x) = sin(x) memiliki fungsi invers f^-1(x) = arcsin(x).
- Fungsi f(x) = e^x memiliki fungsi invers f^-1(x) = ln(x).
Menentukan Fungsi Invers

Fungsi invers adalah fungsi yang membalikkan operasi suatu fungsi. Dengan kata lain, fungsi invers adalah fungsi yang menghasilkan input awal ketika diberikan output fungsi tersebut.
Untuk menentukan fungsi invers suatu fungsi, kita dapat mengikuti langkah-langkah berikut:
Langkah-langkah Menentukan Fungsi Invers
- Tukar posisi variabel x dan y pada persamaan fungsi.
- Selesaikan persamaan baru untuk y.
- Ganti nama variabel y dengan f-1(x) untuk menunjukkan fungsi invers.
Berikut adalah beberapa contoh fungsi dan fungsi inversnya:
| Fungsi | Fungsi Invers |
|---|---|
| f(x) = 2x + 1 | f-1(x) = (x
|
| f(x) = x 2 (x ≥ 0) | f -1 (x) = √x |
| f(x) = sin x | f -1 (x) = arcsin x |
Aplikasi Fungsi Invers

Fungsi invers memiliki aplikasi luas dalam berbagai bidang kehidupan nyata.
Contoh Soal Terapan
Misalkan sebuah perusahaan ingin memodelkan hubungan antara jumlah produk yang dijual (y) dan harga per unit (x). Perusahaan menentukan bahwa hubungan tersebut dapat dimodelkan oleh fungsi y = 100
5x.
Jika perusahaan ingin menentukan harga per unit yang menghasilkan penjualan 60 unit, mereka dapat menggunakan fungsi invers:x = (100
y)/5
x = (100
60)/5
x = 8Oleh karena itu, perusahaan harus menetapkan harga per unit sebesar Rp8 untuk mencapai penjualan 60 unit.
Contoh Soal dan Pembahasan

Dalam materi fungsi invers, siswa akan mempelajari konsep invers fungsi dan cara menentukannya. Untuk mengasah pemahaman tersebut, berikut adalah beberapa contoh soal dan pembahasannya.
Soal 1
Tentukan invers fungsi f(x) = 2x – 3.
Pembahasan:
- Tukar variabel x dan y: y = 2x
3.
Soal 2
Tentukan invers fungsi g(x) = x 3 + 1.
Pembahasan:
- Tukar variabel x dan y: y = x3 + 1.
- Kurangi 1 dari kedua sisi: y
1 = x 3 .
1) 1/3 .
1) 1/3 .
Soal 3
Tentukan invers fungsi h(x) = (x – 2)/(x + 1).
Pembahasan:
- Tukar variabel x dan y: y = (x
2)/(x + 1).
- y)/(1
- y).
- x)/(1
- x).
Kesalahan Umum
Siswa sering membuat kesalahan saat mengerjakan soal fungsi invers. Kesalahan umum ini dapat memengaruhi akurasi dan pemahaman mereka tentang konsep fungsi invers.
Berikut adalah beberapa kesalahan umum yang perlu dihindari:
Mengganti f(x) dengan x
Saat mencari invers fungsi, penting untuk mengganti f(x) dengan y dan bukan x. Misalnya, jika f(x) = 2x + 1, maka inversnya adalah f^-1(y) = (y – 1)/2, bukan f^-1(x) = 2x + 1.
Tidak membalikkan operasi
Fungsi invers membalikkan operasi yang dilakukan oleh fungsi asli. Jika fungsi aslinya menjumlahkan 3, maka inversnya harus mengurangkan 3. Misalnya, jika f(x) = x + 3, maka f^-1(x) = x – 3.
Menghitung invers fungsi yang tidak memiliki invers
Tidak semua fungsi memiliki invers. Fungsi harus satu-satu (injektif) dan onto (surjektif) untuk memiliki invers. Misalnya, fungsi f(x) = x^2 tidak memiliki invers karena tidak satu-satu.
Tips untuk Menghindari Kesalahan
Untuk menghindari kesalahan ini, siswa harus mengikuti beberapa tips:
- Selalu ingat untuk mengganti f(x) dengan y saat mencari invers.
- Identifikasi operasi yang dilakukan oleh fungsi asli dan balikkan operasi tersebut.
- Periksa apakah fungsi tersebut satu-satu dan onto sebelum mencari invers.
Akhir Kata
Memahami fungsi invers sangat penting untuk memecahkan berbagai masalah matematika, fisika, dan bidang lainnya. Dengan memahami konsep dasar, sifat, dan cara menentukan fungsi invers, siswa dapat meningkatkan kemampuan mereka dalam menyelesaikan masalah yang melibatkan konsep ini. Artikel ini diharapkan dapat memberikan panduan yang komprehensif dan membantu siswa dalam memahami topik fungsi invers dengan lebih baik.
Jawaban yang Berguna
Apa itu fungsi invers?
Fungsi invers adalah fungsi yang membalikkan fungsi aslinya, sehingga nilai input dan output dari fungsi asli dipertukarkan.
Bagaimana cara menentukan fungsi invers?
Untuk menentukan fungsi invers, kita dapat menukar variabel input dan output, kemudian menyelesaikan persamaan yang dihasilkan untuk variabel input.
Apa saja sifat-sifat fungsi invers?
Sifat-sifat fungsi invers antara lain:
