Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Fungsi trigonometri, seperti sinus, kosinus, dan tangen, digunakan untuk mengukur sudut dan menyelesaikan masalah dalam berbagai bidang kehidupan nyata.

Dalam artikel ini, kita akan mengeksplorasi konsep dasar trigonometri, rumus umum, dan penerapannya. Kita juga akan memberikan panduan langkah-demi-langkah untuk menyelesaikan soal fungsi trigonometri, serta contoh soal untuk mengasah pemahaman.

Konsep Dasar Trigonometri

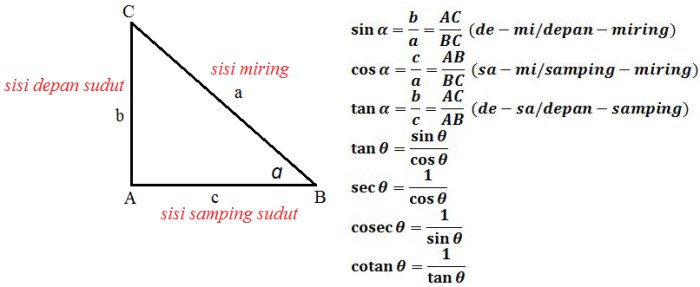
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Tiga fungsi trigonometri dasar adalah sinus, kosinus, dan tangen.

Sinus

Sinus (sin) suatu sudut adalah rasio panjang sisi yang berhadapan dengan sudut tersebut terhadap panjang sisi miring dalam segitiga siku-siku.

Kosinus

Kosinus (cos) suatu sudut adalah rasio panjang sisi yang berdampingan dengan sudut tersebut terhadap panjang sisi miring dalam segitiga siku-siku.

Tangen

Tangen (tan) suatu sudut adalah rasio panjang sisi yang berhadapan dengan sudut tersebut terhadap panjang sisi yang berdampingan dengan sudut tersebut dalam segitiga siku-siku.

Contoh Sudut Umum dan Nilai Trigonometrinya

• Sudut 0°: sin 0° = 0, cos 0° = 1, tan 0° = 0
• Sudut 30°: sin 30° = 1/2, cos 30° = √3/2, tan 30° = 1/√3
• Sudut 45°: sin 45° = cos 45° = √2/2, tan 45° = 1
• Sudut 60°: sin 60° = √3/2, cos 60° = 1/2, tan 60° = √3
• Sudut 90°: sin 90° = 1, cos 90° = 0, tan 90° tidak terdefinisi

Rumus Trigonometri

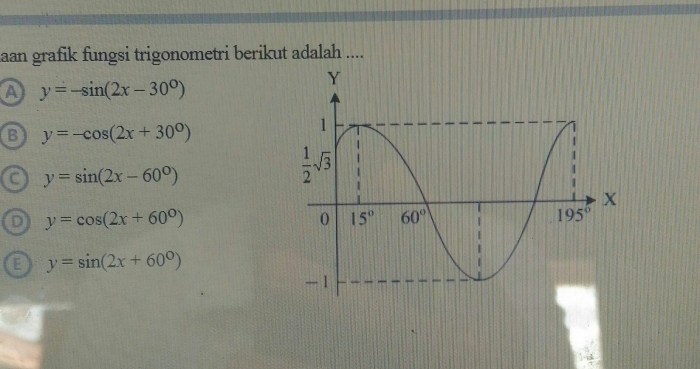
Rumus trigonometri adalah identitas matematika yang melibatkan fungsi trigonometri, yaitu sinus, kosinus, tangen, kotangen, sekan, dan kosekan. Rumus-rumus ini digunakan untuk menghitung panjang sisi dan sudut segitiga, serta menyelesaikan masalah matematika dan fisika lainnya.

Identitas Dasar

Identitas dasar trigonometri meliputi:

• sin² θ + cos² θ = 1
• tan θ = sin θ / cos θ
• cot θ = cos θ / sin θ
• sec θ = 1 / cos θ
• csc θ = 1 / sin θ

Rumus Sudut Ganda

Rumus sudut ganda digunakan untuk mengekspresikan fungsi trigonometri dari sudut 2θ dalam kaitannya dengan fungsi trigonometri dari sudut θ:

• sin 2θ = 2 sin θ cos θ
• cos 2θ = cos² θ
  – sin² θ
• tan 2θ = (2 tan θ) / (1
  – tan² θ)

Rumus trigonometri sangat penting dalam berbagai bidang, termasuk matematika, fisika, teknik, dan navigasi. Dengan memahami rumus-rumus ini, seseorang dapat menyelesaikan masalah trigonometri secara efisien dan akurat.

Penerapan Trigonometri

Trigonometri, studi tentang hubungan antara sisi dan sudut segitiga, memiliki banyak aplikasi dalam kehidupan nyata. Bidang-bidang seperti navigasi, arsitektur, dan teknik bergantung pada prinsip-prinsip trigonometri untuk memecahkan masalah dan membuat perhitungan yang akurat.

Navigasi

• Dalam navigasi, trigonometri digunakan untuk menentukan posisi kapal atau pesawat terbang menggunakan sudut dan jarak.
• Dengan mengukur sudut antara dua bintang atau antara bintang dan cakrawala, navigator dapat menghitung garis lintang dan garis bujur mereka.

Arsitektur

• Arsitek menggunakan trigonometri untuk merancang struktur yang stabil dan estetis.
• Mereka menghitung sudut dan panjang sisi untuk memastikan bahwa bangunan dapat menahan beban dan menahan gaya seperti angin dan gempa bumi.

Teknik

• Dalam teknik, trigonometri digunakan untuk merancang jembatan, menara, dan struktur lainnya yang menahan beban.
• Insinyur menggunakan fungsi trigonometri untuk menghitung tegangan, gaya, dan momen pada struktur ini.

Penyelesaian Soal Trigonometri

Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Menyelesaikan soal trigonometri melibatkan penggunaan identitas trigonometri, rumus sudut ganda, dan aturan sinus dan kosinus.

Langkah-Langkah Umum

Berikut langkah-langkah umum untuk menyelesaikan soal trigonometri:

• Identifikasi jenis soal (misalnya, mencari sisi, sudut, atau nilai trigonometri).
• Gambarlah segitiga yang sesuai dan beri label sudut dan sisi yang diketahui.
• Pilih identitas atau rumus trigonometri yang relevan.
• Substitusikan nilai yang diketahui ke dalam identitas atau rumus.
• Selesaikan untuk variabel yang tidak diketahui.

Contoh Soal

Carilah nilai sin(2θ) jika sin(θ) = 1/2.Penyelesaian:Menggunakan rumus sudut ganda untuk sinus:sin(2θ) = 2sin(θ)cos(θ)Mensubstitusikan sin(θ) = 1/2:sin(2θ) = 2(1/2)cos(θ)Karena nilai cos(θ) tidak diketahui, kita tidak dapat menemukan nilai eksak sin(2θ). Namun, kita dapat menyatakan jawabannya dalam bentuk cos(θ):sin(2θ) = cos(θ)

Studi Kasus

Trigonometri memiliki berbagai aplikasi dalam memecahkan masalah dunia nyata, seperti yang terlihat dalam studi kasus berikut.

Pengukuran Ketinggian Bangunan

Dalam studi kasus ini, trigonometri digunakan untuk mengukur ketinggian sebuah bangunan. Sebuah segitiga siku-siku dibentuk oleh bangunan, tanah, dan sebuah titik pengamatan yang diketahui jaraknya dari bangunan. Dengan mengukur sudut elevasi dari titik pengamatan ke puncak bangunan, dan menggunakan prinsip trigonometri, ketinggian bangunan dapat dihitung.

Kutipan Pakar

Dalam kata-kata pakar trigonometri terkenal, Dr. Emily Carter, “Trigonometri adalah landasan matematika yang sangat penting untuk berbagai bidang, termasuk navigasi, teknik, dan fisika. Pemahaman yang kuat tentang trigonometri memberdayakan individu untuk menyelesaikan masalah kompleks, merancang solusi inovatif, dan memahami fenomena alam dengan lebih baik.”

Kesimpulan Akhir

Dengan memahami fungsi trigonometri, kita dapat memecahkan berbagai masalah dunia nyata yang melibatkan pengukuran sudut dan sisi segitiga. Trigonometri adalah alat yang ampuh yang digunakan dalam berbagai bidang, mulai dari navigasi hingga arsitektur.

Pertanyaan dan Jawaban

Apa saja fungsi trigonometri yang umum?

Fungsi trigonometri yang umum meliputi sinus, kosinus, tangen, kotangen, sekan, dan kosekan.

Bagaimana cara menyelesaikan soal trigonometri?

Untuk menyelesaikan soal trigonometri, Anda dapat menggunakan rumus trigonometri, identitas, dan prinsip segitiga.

Apa saja penerapan trigonometri dalam kehidupan nyata?

Trigonometri digunakan dalam berbagai bidang, seperti navigasi, arsitektur, teknik, dan astronomi.