Dalam dunia fisika, getaran harmonik merupakan fenomena penting yang ditemukan dalam berbagai sistem. Getaran ini ditandai dengan gerakan periodik yang berosilasi di sekitar titik keseimbangan. Contoh umum getaran harmonik termasuk ayunan pendulum, pegas yang berosilasi, dan gelombang suara.

Memahami getaran harmonik sangat penting untuk banyak bidang, mulai dari fisika hingga teknik. Dengan mempelajari konsep dasar, persamaan gerak, dan aplikasi getaran harmonik, kita dapat memperoleh wawasan tentang berbagai fenomena alam dan teknologi.

Pengertian Getaran Harmonik

Getaran harmonik adalah gerakan periodik di mana suatu sistem berosilasi di sekitar titik kesetimbangan dengan amplitudo konstan dan frekuensi sudut yang konstan.

Dalam getaran harmonik, sistem akan kembali ke titik yang sama secara berulang dengan interval waktu yang teratur. Gerakan ini dapat digambarkan sebagai fungsi sinusoidal waktu.

Contoh Getaran Harmonik

• Ayunan bandul
• Pegas yang bergetar
• Gelombang bunyi
• Gelombang cahaya

Persamaan Gerak Getaran Harmonik

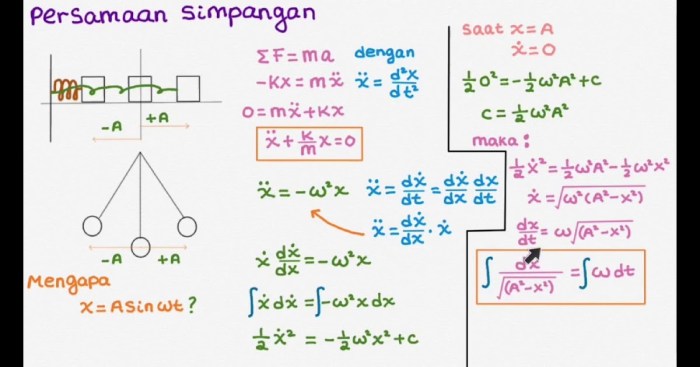
Gerakan harmonik merupakan jenis gerak periodik yang ditandai dengan amplitudo, frekuensi, dan fase tertentu. Persamaan gerak getaran harmonik menjelaskan hubungan antara besaran-besaran tersebut dengan perpindahan benda yang bergetar.

Secara umum, persamaan gerak getaran harmonik dapat dituliskan sebagai berikut:

$$x(t) = A\cos(\omega t + \phi)$$

di mana:

• x(t) adalah perpindahan benda pada waktu t
• A adalah amplitudo getaran
• ω adalah frekuensi sudut getaran
• t adalah waktu
• φ adalah fase awal getaran

Parameter-parameter yang memengaruhi persamaan gerak getaran harmonik adalah:

• Amplitudo (A): Jarak maksimum benda dari titik kesetimbangan.
• Frekuensi Sudut (ω): Kecepatan sudut benda yang bergetar, diukur dalam radian per detik.
• Frekuensi (f): Jumlah getaran yang dilakukan benda dalam satu detik, diukur dalam Hertz (Hz). (ω = 2πf)
• Fase Awal (φ): Posisi benda pada waktu t = 0, diukur dalam radian.

Grafik Gerakan Getaran Harmonik

Grafik gerakan getaran harmonik menggambarkan perubahan posisi suatu benda yang bergetar harmonik terhadap waktu. Grafik ini berbentuk sinusoida, dengan sumbu vertikal mewakili posisi benda dan sumbu horizontal mewakili waktu.

Grafik gerakan getaran harmonik memiliki beberapa parameter penting, yaitu:

• Amplitudo (A): Jarak maksimum benda dari titik kesetimbangan.
• Periode (T): Waktu yang diperlukan benda untuk menyelesaikan satu siklus getaran.
• Frekuensi (f): Jumlah siklus getaran per satuan waktu.
• Fase awal (phi): Posisi benda pada saat waktu t = 0.

Persamaan Grafik Gerakan Getaran Harmonik

Persamaan grafik gerakan getaran harmonik diberikan oleh:

x(t) = A cos(2πft + phi)

di mana:

• x(t) adalah posisi benda pada waktu t
• A adalah amplitudo
• f adalah frekuensi
• t adalah waktu
• phi adalah fase awal

Aplikasi Getaran Harmonik

Getaran harmonik memiliki aplikasi yang luas dalam berbagai bidang, termasuk fisika, teknik, dan kedokteran. Keuntungan utama menggunakan getaran harmonik dalam aplikasi ini adalah kesederhanaan, prediktabilitas, dan kemudahan kontrolnya.

Namun, ada juga keterbatasan penggunaan getaran harmonik, seperti amplitudo yang terbatas dan frekuensi resonansi yang dapat menyebabkan kegagalan sistem.

Fisika

• Pegas dan bandul: Getaran harmonik pada pegas dan bandul digunakan untuk mengukur waktu dan menentukan sifat fisik material.
• Gelombang: Getaran harmonik adalah dasar dari semua jenis gelombang, seperti gelombang suara dan cahaya.
• Resonansi: Getaran harmonik dapat digunakan untuk menciptakan resonansi, yang dapat digunakan untuk memecah batu atau menghasilkan suara yang nyaring.

Teknik

• Mesin: Getaran harmonik digunakan dalam mesin untuk menggerakkan piston dan roda gila.
• Struktur: Getaran harmonik digunakan untuk menganalisis dan merancang struktur agar tahan terhadap gempa bumi dan angin kencang.
• Alat musik: Getaran harmonik pada senar dan kolom udara menghasilkan suara dalam alat musik.

Kedokteran

• Ultrasonografi: Getaran harmonik digunakan dalam ultrasonografi untuk menghasilkan gambar organ dan jaringan internal tubuh.
• Terapi fisik: Getaran harmonik digunakan dalam terapi fisik untuk meredakan nyeri dan meningkatkan mobilitas.
• Perawatan gigi: Getaran harmonik digunakan dalam perawatan gigi untuk menghilangkan plak dan karang gigi.

Penyelesaian Soal Getaran Harmonik

Penyelesaian soal getaran harmonik melibatkan langkah-langkah sistematis untuk menentukan parameter gerak osilasi harmonik.

Langkah-langkah Penyelesaian Soal Getaran Harmonik

1. Identifikasi amplitudo (A), frekuensi sudut (ω), dan fase awal (φ) dari gerak.
2. Tulis persamaan perpindahan (x) sebagai fungsi waktu (t): x = A cos(ωt + φ).
3. Hitung kecepatan (v) dan percepatan (a) sebagai fungsi waktu menggunakan turunan persamaan perpindahan.
4. Tentukan energi potensial (U) dan energi kinetik (K) sebagai fungsi waktu.
5. Analisis grafik perpindahan, kecepatan, dan percepatan terhadap waktu untuk memahami karakteristik gerak.

Contoh Soal dan Pembahasan

Soal:Sebuah benda bergetar harmonik dengan amplitudo 10 cm dan frekuensi 5 Hz. Jika pada saat t = 0 benda berada pada posisi kesetimbangan dengan kecepatan positif, tentukan:a. Persamaan perpindahanb. Kecepatan dan percepatan pada t = 0,5 sc. Energi potensial dan energi kinetik pada t = 1 sPembahasan:a.

Persamaan perpindahan:x = A cos(ωt + φ) = 10 cos(2π(5)t + 0) = 10 cos(10πt)b. Kecepatan pada t = 0,5 s:v =

• ωA sin(ωt + φ) =
• 2π(5)(10) sin(10π(0,5)) =
• 100π cm/s

Percepatan pada t = 0,5 s:a =

• ω²A cos(ωt + φ) =
• (2π(5))²(10) cos(10π(0,5)) =
• 500π² cm/s²

c. Energi potensial pada t = 1 s:U = (1/2)kA² cos²(ωt + φ) = (1/2)(k)(10)² cos²(10π(1)) = (1/2)(k)(100) JEnergi kinetik pada t = 1 s:K = (1/2)mv² = (1/2)m(100π)² cm²/s² = (1/2)(m)(10000π²) J

Pengaruh Faktor Eksternal pada Getaran Harmonik

Getaran harmonik dipengaruhi oleh faktor eksternal yang dapat mengubah karakteristiknya. Dua faktor eksternal utama adalah gaya redaman dan gaya pegas.

Gaya Redaman

Gaya redaman berlawanan arah dengan arah getaran dan bekerja untuk mengurangi amplitudo getaran. Ini terjadi karena adanya hambatan, seperti gesekan atau hambatan udara.

• Redaman linier: Gaya redaman sebanding dengan kecepatan getaran.
• Redaman kuadrat: Gaya redaman sebanding dengan kuadrat kecepatan getaran.

Gaya redaman menyebabkan penurunan amplitudo secara bertahap, yang akhirnya menghentikan getaran.

Gaya Pegas

Gaya pegas adalah gaya elastis yang mengembalikan sistem ke posisi kesetimbangannya. Kekuatan gaya pegas sebanding dengan besar perpindahan dari posisi kesetimbangan.

• Pegas linear: Gaya pegas sebanding dengan perpindahan.
• Pegas non-linear: Gaya pegas tidak sebanding dengan perpindahan.

Gaya pegas mempengaruhi frekuensi getaran. Semakin kuat gaya pegas, semakin tinggi frekuensi getaran.

Penutup

Pemahaman tentang getaran harmonik tidak hanya terbatas pada bidang akademis tetapi juga memiliki implikasi praktis yang luas. Dengan menguasai konsep ini, kita dapat merancang dan menganalisis sistem yang melibatkan osilasi, getaran, dan gelombang. Kemampuan ini sangat penting dalam berbagai bidang, termasuk fisika, teknik, dan kedokteran, yang memungkinkan kita untuk mengembangkan teknologi baru dan memecahkan masalah dunia nyata.

Pertanyaan Umum yang Sering Muncul

Apa perbedaan antara getaran harmonik dan getaran non-harmonik?

Getaran harmonik ditandai dengan gerakan periodik sinusoidal, sedangkan getaran non-harmonik memiliki bentuk gelombang yang lebih kompleks dan tidak teratur.

Bagaimana cara menghitung frekuensi getaran harmonik?

Frekuensi getaran harmonik dapat dihitung menggunakan persamaan f = 1/T, di mana f adalah frekuensi dan T adalah periode getaran.

Apa saja faktor yang mempengaruhi amplitudo getaran harmonik?

Amplitudo getaran harmonik dipengaruhi oleh gaya yang diterapkan, massa benda yang bergetar, dan kekakuan sistem.