Hukum Kepler adalah pilar penting dalam astronomi, yang memberikan kerangka kerja untuk memahami pergerakan benda langit. Dikembangkan oleh Johannes Kepler pada abad ke-17, hukum-hukum ini merevolusi pemahaman kita tentang tata surya dan membentuk dasar bagi fisika modern.
Artikel ini menyajikan contoh soal dan penjelasan mendalam tentang Hukum Kepler, memberikan wawasan tentang penerapan praktisnya dalam astronomi dan eksplorasi ruang angkasa. Selain itu, kami akan mengeksplorasi batasan hukum-hukum ini dan mengecualikan kasus-kasus khusus yang tidak sesuai dengan prediksinya.
Hukum Kepler I
Hukum Kepler I, juga dikenal sebagai Hukum Orbit Elips, menyatakan bahwa setiap planet bergerak dalam lintasan elips mengelilingi matahari, dengan matahari berada di salah satu fokus elips.
Persamaan matematis untuk Hukum Kepler I adalah:
r = a(1
e cos θ)
di mana:* r adalah jarak planet dari matahari
- a adalah sumbu semi-mayor elips
- e adalah eksentrisitas elips
- θ adalah sudut di pusat elips
Contoh Penerapan
Contoh penerapan Hukum Kepler I dalam kehidupan sehari-hari antara lain:* Perhitungan lintasan satelit dan pesawat ruang angkasa
- Prediksi gerhana matahari dan bulan
- Navigasi antariksa
- Studi tentang evolusi tata surya
Hukum Kepler II
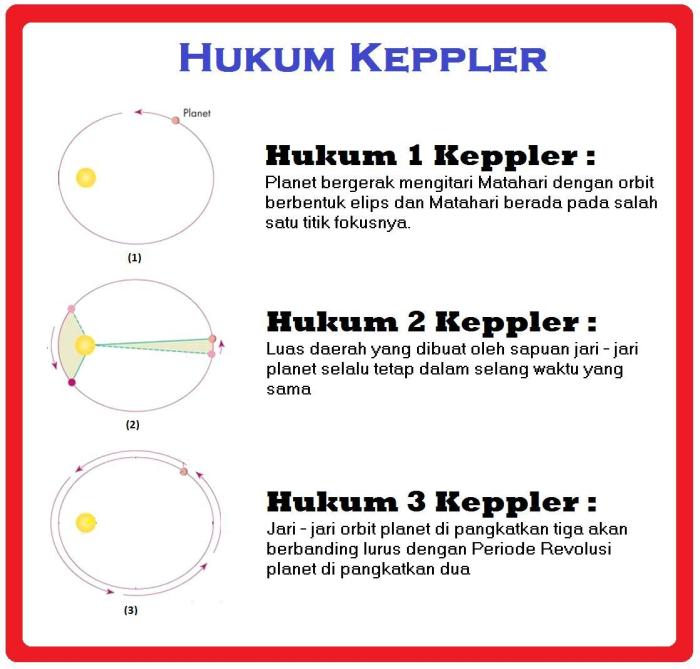
Hukum Kepler II menyatakan bahwa garis yang menghubungkan sebuah planet dengan matahari menyapu luas daerah yang sama dalam selang waktu yang sama. Artinya, kecepatan orbit planet bervariasi bergantung pada jaraknya dari matahari.
Hubungan Kecepatan Orbit dan Jarak dari Matahari
Ketika sebuah planet berada pada jarak yang lebih dekat dengan matahari, kecepatan orbitnya lebih tinggi. Sebaliknya, ketika planet berada pada jarak yang lebih jauh dari matahari, kecepatan orbitnya lebih rendah. Ini karena gaya gravitasi matahari berkurang dengan bertambahnya jarak. Oleh karena itu, planet yang lebih dekat dengan matahari mengalami gaya gravitasi yang lebih kuat dan karenanya bergerak lebih cepat dalam orbitnya.
Hukum Kepler III
Hukum Kepler III, juga dikenal sebagai Hukum Harmonik, menetapkan hubungan antara periode orbit planet dengan jarak rata-ratanya dari matahari.
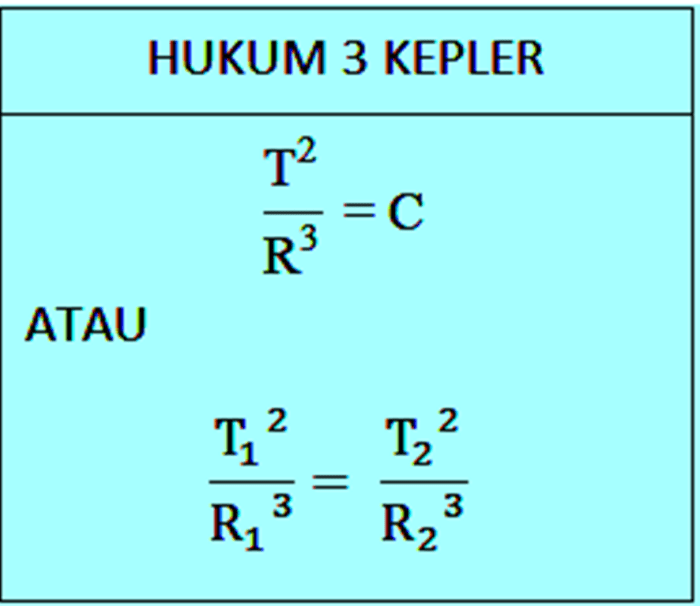
Hukum ini menyatakan bahwa kuadrat periode orbit (T²) suatu planet berbanding lurus dengan pangkat tiga jarak rata-ratanya (r³) dari matahari.
Data Periode Orbit dan Jarak Rata-rata Planet
Berikut adalah tabel yang merangkum data tentang periode orbit dan jarak rata-rata planet-planet dari matahari:
| Planet | Periode Orbit (tahun) | Jarak Rata-rata dari Matahari (AU) |
|---|---|---|
| Merkurius | 0,24 | 0,39 |
| Venus | 0,62 | 0,72 |
| Bumi | 1,00 | 1,00 |
| Mars | 1,88 | 1,52 |
| Jupiter | 11,86 | 5,20 |
| Saturnus | 29,46 | 9,54 |
| Uranus | 84,01 | 19,22 |
| Neptunus | 164,88 | 30,11 |
Grafik Hubungan Periode Orbit dan Jarak dari Matahari
Grafik berikut menunjukkan hubungan antara periode orbit dan jarak dari matahari untuk planet-planet yang tercantum dalam tabel:
[Tampilkan grafik yang menunjukkan hubungan antara periode orbit dan jarak dari matahari]
Implikasi Hukum Kepler III bagi Sistem Tata Surya
Hukum Kepler III memiliki implikasi penting bagi sistem tata surya:
- Ini menunjukkan bahwa planet-planet di tata surya bergerak dalam orbit elips, dengan matahari di salah satu fokusnya.
- Ini menjelaskan mengapa planet-planet bagian dalam memiliki periode orbit yang lebih pendek daripada planet-planet bagian luar.
- Ini membantu menentukan massa matahari dan planet-planet di tata surya.
- Ini digunakan untuk memprediksi periode orbit planet-planet baru yang ditemukan di luar tata surya.
Penerapan Hukum Kepler
Hukum Kepler merupakan dasar penting dalam astronomi, memberikan kerangka untuk memahami dan memprediksi pergerakan benda-benda langit.
Hukum-hukum ini telah diterapkan secara luas dalam berbagai bidang astronomi, termasuk menentukan orbit benda langit dan merencanakan eksplorasi ruang angkasa.
Penentuan Orbit Benda Langit
Hukum Kepler sangat penting dalam menentukan orbit benda langit. Hukum pertama Kepler menyatakan bahwa setiap planet bergerak mengelilingi matahari dalam lintasan elips, dengan matahari berada pada salah satu fokus elips.
Dengan menggunakan hukum ini, para astronom dapat menentukan bentuk dan ukuran orbit benda langit, serta memprediksi posisinya pada waktu tertentu.
Eksplorasi Ruang Angkasa
Hukum Kepler juga berperan penting dalam eksplorasi ruang angkasa. Hukum kedua Kepler menyatakan bahwa garis yang menghubungkan sebuah planet ke matahari menyapu area yang sama dalam selang waktu yang sama.
Hukum ini memungkinkan para ilmuwan menghitung kecepatan benda langit dan merencanakan lintasan pesawat ruang angkasa untuk mencapai tujuannya dengan efisien.
Batasan Hukum Kepler

Hukum Kepler merupakan representasi yang sangat baik untuk menggambarkan gerakan benda langit dalam tata surya. Namun, terdapat beberapa batasan yang perlu dipertimbangkan.
Batasan utama dari Hukum Kepler adalah pengaruh gangguan dari benda langit lain. Hukum Kepler mengasumsikan bahwa benda langit bergerak dalam ruang hampa tanpa pengaruh gaya dari benda lain. Namun, dalam kenyataannya, benda langit saling memengaruhi melalui gaya gravitasi.
Pengaruh Gangguan dari Benda Langit Lain
Gangguan dari benda langit lain dapat menyebabkan penyimpangan dari Hukum Kepler. Misalnya, pengaruh gravitasi dari planet-planet lain dapat menyebabkan perubahan eksentrisitas dan kemiringan orbit suatu planet.
Pengecualian dan Kasus Khusus
Selain gangguan dari benda langit lain, terdapat beberapa pengecualian dan kasus khusus yang tidak sesuai dengan Hukum Kepler.
- Orbit Sangat Eksentrik: Hukum Kepler bekerja dengan baik untuk orbit yang hampir melingkar. Namun, untuk orbit yang sangat eksentrik, penyimpangan dari Hukum Kepler menjadi lebih signifikan.
- Benda Langit Non-Sferis: Hukum Kepler mengasumsikan bahwa benda langit berbentuk bola. Namun, beberapa benda langit, seperti asteroid, memiliki bentuk yang tidak beraturan. Hal ini dapat menyebabkan penyimpangan dari Hukum Kepler.
- Relativitas Umum: Dalam kasus di mana kecepatan benda langit mendekati kecepatan cahaya, Hukum Kepler tidak lagi akurat. Relativitas umum harus digunakan untuk menjelaskan gerakan benda langit dalam kondisi ini.
Kesimpulan
Hukum Kepler memberikan dasar yang kuat untuk memahami pergerakan benda langit dan membentuk landasan bagi penemuan ilmiah lebih lanjut. Dengan memberikan kerangka kerja yang dapat diandalkan, hukum-hukum ini telah memainkan peran penting dalam pengembangan astronomi dan terus menginspirasi eksplorasi ruang angkasa hingga hari ini.
Pertanyaan Umum (FAQ)
Bagaimana cara menerapkan Hukum Kepler I untuk menentukan jarak planet dari Matahari?
Gunakan persamaan r = a(1 – e²) / (1 + e cosθ), di mana r adalah jarak planet dari Matahari, a adalah sumbu semi-mayor, e adalah eksentrisitas orbit, dan θ adalah sudut sejati.
Bagaimana hubungan antara kecepatan orbit dan jarak dari Matahari menurut Hukum Kepler II?
Kecepatan orbit planet berbanding terbalik dengan akar kuadrat jaraknya dari Matahari.
Bagaimana Hukum Kepler III digunakan untuk memprediksi periode orbit komet?
Dengan mengetahui jarak rata-rata komet dari Matahari, periode orbitnya dapat diperkirakan menggunakan persamaan T² ∝ r³, di mana T adalah periode orbit dan r adalah jarak rata-rata.
