Contoh soal integral substitusi trigonometri merupakan bagian penting dalam kalkulus, menyediakan teknik untuk menyelesaikan integral yang melibatkan fungsi trigonometri. Dengan memahami konsep dan jenis substitusi trigonometri, individu dapat menguasai teknik ini untuk memecahkan berbagai masalah kalkulus.

Substitusi trigonometri menawarkan banyak manfaat, seperti menyederhanakan integral yang kompleks, memungkinkan integrasi fungsi rasional, dan membantu menyelesaikan integral yang tidak dapat diselesaikan dengan metode lain.

Pemahaman Substitusi Trigonometri

Substitusi trigonometri adalah teknik yang digunakan dalam kalkulus integral untuk menyederhanakan integral yang melibatkan fungsi trigonometri. Dengan mengganti variabel integrasi dengan fungsi trigonometri, kita dapat mengubah integral menjadi bentuk yang lebih mudah diselesaikan.

Sebagai contoh, jika kita memiliki integral ∫ sin(x) dx, kita dapat mengganti variabel integrasi dengan u = cos(x). Dengan menggunakan aturan rantai, kita mendapatkan du =-sin(x) dx . Dengan demikian, integral menjadi ∫-du = -u + C = -cos(x) + C .

Manfaat Substitusi Trigonometri

• Menyederhanakan integral yang melibatkan fungsi trigonometri.
• Memungkinkan kita menggunakan teknik integrasi yang lebih sederhana.
• Dapat mengarah pada solusi yang lebih akurat dan efisien.

Jenis Substitusi Trigonometri

Dalam integral trigonometri, substitusi trigonometri digunakan untuk menyederhanakan integral dengan menggantikan ekspresi trigonometri yang kompleks dengan variabel baru.

Terdapat tiga jenis utama substitusi trigonometri:

Substitusi Sinus

• Digunakan ketika integran mengandung sin xatau cos x.
• Substitusi: u = sin xatau u = cos x
• Rumus: du = cos x dxatau du =-sin x dx
• Contoh: ∫ sin²x dx = ∫ u ²du = (1/3)u ³+ C = (1/3)sin ³x + C

Substitusi Tangent

• Digunakan ketika integran mengandung tan xatau cot x.
• Substitusi: u = tan xatau u = cot x
• Rumus: du = sec²x dx atau du =-csc ²x dx
• Contoh: ∫ tan³x dx = ∫ u ³du = (1/4)u ⁴+ C = (1/4)tan ⁴x + C

Substitusi Pitagoras

• Digunakan ketika integran mengandung sin²x , cos²x , atau tan²x .
• Substitusi: u = sin x, u = cos x, atau u = tan x
• Rumus: u²= 1 – u ²
• Contoh: ∫ sin²x dx = ∫ u ²du = (1/3)u ³+ C = (1/3)sin ³x + C

Cara Menggunakan Substitusi Trigonometri

Substitusi trigonometri adalah teknik integral yang menggunakan identitas trigonometri untuk menyederhanakan integral. Teknik ini sangat berguna untuk integral yang melibatkan fungsi trigonometri.

Langkah-langkah Menggunakan Substitusi Trigonometri

• Identifikasi fungsi trigonometri dalam integral.
• Pilih substitusi yang sesuai berdasarkan fungsi trigonometri yang diidentifikasi.
• Gunakan identitas trigonometri untuk mengekspresikan fungsi trigonometri dalam bentuk substitusi.
• Tentukan diferensial substitusi.
• Substitusikan ekspresi baru ke dalam integral dan sederhanakan.
• Integralkan fungsi yang disederhanakan.
• Substitusikan kembali substitusi asli untuk mendapatkan integral asli.

Contoh Langkah demi Langkah

Misalkan kita ingin mengintegralkan sin(x) cos(x) dx. Kita dapat menggunakan substitusi u = sin(x).

Dalam menyelesaikan contoh soal integral substitusi trigonometri, terkadang kita memerlukan pengetahuan tambahan seperti rumus trigonometri. Seperti halnya pada majalah anak yang memiliki kolom khusus, misalnya sebutkan contoh kolom khusus majalah anak , yang memuat informasi menarik dan edukatif. Begitu pula dalam integral substitusi trigonometri, kita perlu memahami substitusi yang tepat agar dapat menyelesaikan integral dengan benar.

Diferensial substitusi adalah du = cos(x) dx.

Substitusikan ke dalam integral:

∫ sin(x) cos(x) dx = ∫ u du

Contoh soal integral substitusi trigonometri melibatkan penyederhanaan ekspresi trigonometri untuk memfasilitasi integrasi. Perintah untuk membuat teks berjalan adalah teknik pemrograman yang memungkinkan teks bergerak pada layar, yang dapat digunakan untuk menampilkan contoh soal atau solusi integral substitusi trigonometri secara dinamis dan interaktif.

Integralkan:

∫ u du = u^2/2 + C

Substitusikan kembali u = sin(x):

∫ sin(x) cos(x) dx = sin^2(x)/2 + C

Tips Efektif Menggunakan Substitusi Trigonometri, Contoh soal integral substitusi trigonometri

• Pilih substitusi yang paling sesuai untuk fungsi trigonometri yang diberikan.
• Pastikan untuk mengekspresikan fungsi trigonometri dalam bentuk substitusi dengan benar.
• Hati-hati dengan tanda dan rentang substitusi.
• Ingat identitas trigonometri yang relevan untuk substitusi.

Contoh Soal Integral Substitusi Trigonometri

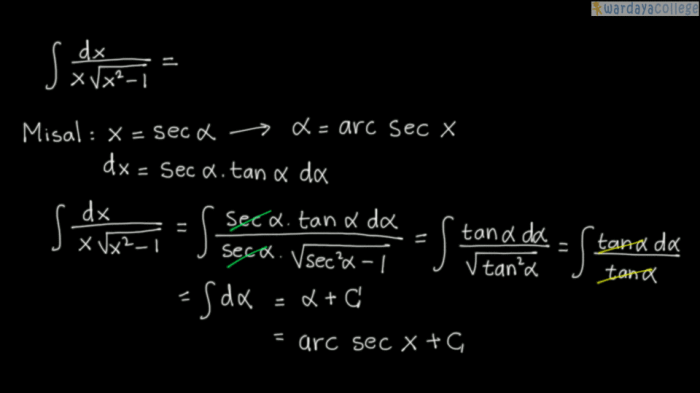
Substitusi trigonometri adalah teknik integrasi yang digunakan untuk menyelesaikan integral yang melibatkan fungsi trigonometri. Teknik ini menggantikan variabel integral dengan fungsi trigonometri, sehingga integral menjadi lebih mudah diselesaikan.

Contoh Soal 1

Hitung integral:

$$\int \sin^2 x \cos x dx$$

Solusi:

1. Substitusikan u = sin x, sehingga du = cos x dx
2. Tulis integral dalam bentuk u:

$$\int u^2 du$$

3. Selesaikan integral:

$$\fracu^33 + C$$

4. Substitusi kembali u = sin x:

$$\frac\sin^3 x3 + C$$

Contoh Soal 2

Hitung integral:

$$\int \tan x \sec^2 x dx$$

Solusi:

1. Substitusikan u = sec x, sehingga du = sec x tan x dx
2. Tulis integral dalam bentuk u:

$$\int u du$$

3. Selesaikan integral:

$$\fracu^22 + C$$

4. Substitusi kembali u = sec x:

$$\frac\sec^2 x2 + C$$

Contoh Soal 3

Hitung integral:

$$\int \frac1\sqrt1

\cos^2 x dx$$

Solusi:

1. Substitusikan u = cos x, sehingga du =
   

   sin x dx

2. Tulis integral dalam bentuk u:

$$\int \frac1\sqrt1

u^2 (-du)$$

3. Selesaikan integral:

$$\sin^-1 u + C$$

4. Substitusi kembali u = cos x:

$$\sin^-1 (\cos x) + C$$

Aplikasi Substitusi Trigonometri

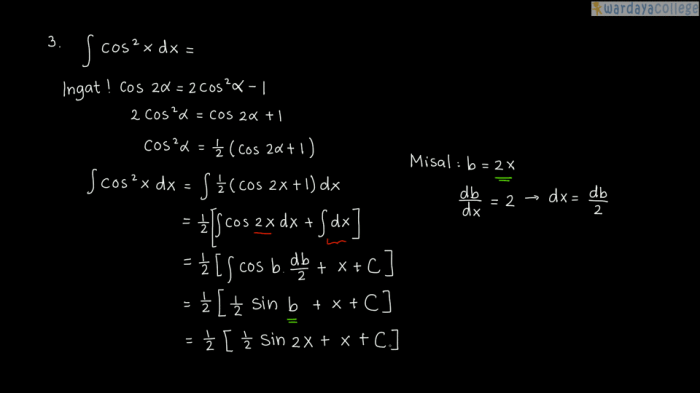
Substitusi trigonometri adalah teknik yang digunakan untuk menyelesaikan integral yang melibatkan fungsi trigonometri. Teknik ini melibatkan penggantian fungsi trigonometri dengan ekspresi aljabar yang setara. Aplikasi substitusi trigonometri sangat luas dan mencakup berbagai bidang.

Fisika

Dalam fisika, substitusi trigonometri digunakan untuk memecahkan masalah yang melibatkan gerak harmonik sederhana, seperti ayunan bandul dan getaran pegas. Dengan mensubstitusikan fungsi sinus atau kosinus untuk posisi atau kecepatan, integral dapat disederhanakan dan diselesaikan.

Teknik

Di bidang teknik, substitusi trigonometri digunakan dalam analisis rangkaian listrik. Dengan mensubstitusikan fungsi trigonometri untuk tegangan atau arus, integral dapat disederhanakan dan diselesaikan untuk menentukan respons rangkaian terhadap sinyal masukan periodik.

Astronomi

Dalam astronomi, substitusi trigonometri digunakan untuk menghitung posisi benda langit. Dengan mensubstitusikan fungsi trigonometri untuk jarak atau sudut, integral dapat disederhanakan dan diselesaikan untuk menentukan orbit planet atau bintang.

Ekonomi

Dalam ekonomi, substitusi trigonometri digunakan untuk menganalisis tren siklik, seperti fluktuasi harga atau tingkat pengangguran. Dengan mensubstitusikan fungsi sinus atau kosinus untuk variabel waktu, integral dapat disederhanakan dan diselesaikan untuk menentukan pola dan tren musiman.

Contoh soal integral substitusi trigonometri banyak dijumpai dalam berbagai bidang keilmuan. Salah satu contohnya adalah menghitung luas daerah di bawah kurva fungsi trigonometri. Di sisi lain, dalam dunia investasi, investor sering kali mempertimbangkan probabilitas kejadian tertentu, seperti berapa probabilitas kejadian jual saham bca . Probabilitas ini dapat membantu investor dalam mengambil keputusan investasi yang tepat.

Kembali pada contoh soal integral substitusi trigonometri, metode ini melibatkan penggantian variabel integral dengan fungsi trigonometri yang sesuai, sehingga integral menjadi lebih mudah diselesaikan.

Akhir Kata

Secara keseluruhan, contoh soal integral substitusi trigonometri memberikan landasan yang kuat untuk memahami teknik penting dalam kalkulus. Dengan menguasai teknik ini, individu dapat mengatasi berbagai masalah kalkulus secara efisien dan efektif, membuka jalan untuk aplikasi yang lebih luas dalam matematika dan bidang lainnya.

Detail FAQ

Apa itu substitusi trigonometri?

Substitusi trigonometri adalah teknik dalam kalkulus yang melibatkan penggantian variabel dalam integral dengan fungsi trigonometri.

Mengapa substitusi trigonometri penting?

Substitusi trigonometri penting karena menyederhanakan integral yang kompleks, memungkinkan integrasi fungsi rasional, dan membantu menyelesaikan integral yang tidak dapat diselesaikan dengan metode lain.

Apa saja jenis-jenis substitusi trigonometri?

Jenis-jenis substitusi trigonometri meliputi substitusi sudut setengah, substitusi sudut ganda, substitusi Pythagoras, dan substitusi Weierstrass.