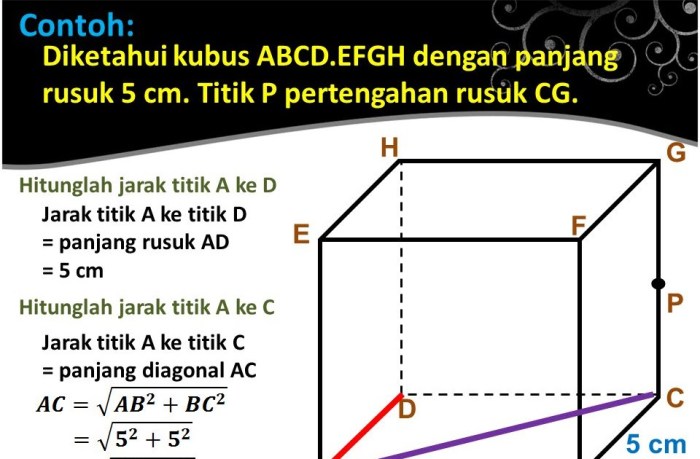
Dalam geometri analitik, jarak antara dua titik pada bidang koordinat memainkan peran penting. Konsep ini membantu kita memahami posisi dan hubungan antar titik dalam ruang dua dimensi.
Rumus jarak yang sederhana memungkinkan kita menentukan jarak antara dua titik apa pun dengan mudah. Rumus ini memiliki berbagai aplikasi praktis dalam bidang seperti navigasi, konstruksi, dan perencanaan kota.
Konsep Jarak Dua Titik
Dalam geometri, jarak antara dua titik pada bidang koordinat adalah ukuran panjang garis lurus yang menghubungkan kedua titik tersebut. Konsep ini digunakan untuk menentukan panjang sisi segitiga, jarak antara objek, dan banyak aplikasi praktis lainnya.
Rumus Jarak
Rumus untuk menghitung jarak antara dua titik (x1, y1) dan (x2, y2) adalah:
d = √((x2
- x1)² + (y2
- y1)²)
di mana:
- d adalah jarak antara kedua titik
- x1 dan y1 adalah koordinat titik pertama
- x2 dan y2 adalah koordinat titik kedua
Contoh
Misalkan kita memiliki dua titik A(2, 3) dan B(5, 7). Jarak antara kedua titik tersebut adalah:
d = √((5
- 2)² + (7
- 3)²)
= √(3² + 4²)= √(9 + 16)= √25= 5
Jadi, jarak antara titik A dan B adalah 5 satuan.
Rumus Jarak
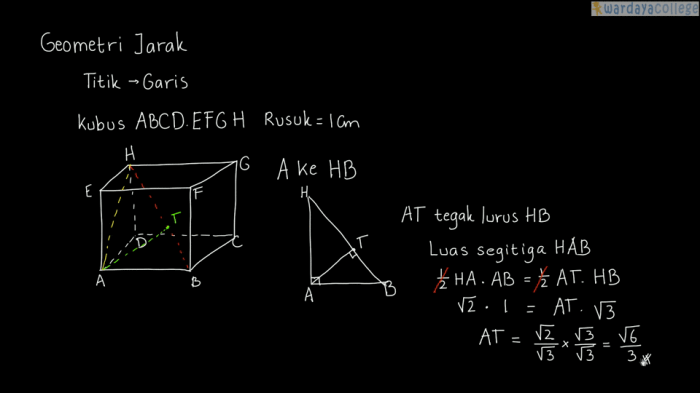
Dalam geometri, rumus jarak digunakan untuk menghitung jarak antara dua titik pada bidang koordinat. Rumus ini penting untuk menyelesaikan berbagai masalah, seperti menentukan panjang garis, luas segitiga, dan volume bangun ruang.
Penggunaan Rumus Jarak
Rumus jarak digunakan dengan cara sebagai berikut:
- Tentukan koordinat kedua titik pada bidang koordinat.
- Kurangkan koordinat titik kedua dari koordinat titik pertama untuk setiap sumbu.
- Kuadratkan selisih yang diperoleh pada setiap sumbu.
- Jumlahkan kuadrat selisih tersebut.
- Hitung akar kuadrat dari jumlah yang diperoleh.
Hasil perhitungan tersebut merupakan jarak antara kedua titik.
Contoh Soal

Berikut adalah beberapa contoh soal jarak antara dua titik beserta koordinat, rumus yang digunakan, dan jawabannya:
Tabel Contoh Soal Jarak Antara Dua Titik
| Koordinat Titik 1 | Koordinat Titik 2 | Rumus | Jawaban |
|---|---|---|---|
| (2, 3) | (5, 7) | d = √[(x2
|
5 |
| (-3, 1) | (1,
|
d = √[(x2
|
8 |
| (0, 0) | (4, 3) | d = √[(x2
|
5 |
Langkah-Langkah Menghitung Jarak
Menghitung jarak antara dua titik pada bidang koordinat adalah proses sederhana yang dapat dilakukan dengan mengikuti langkah-langkah berikut:
Menemukan Perbedaan Koordinat
- Tentukan koordinat kedua titik, yaitu (x1, y1) dan (x2, y2).
- Hitung selisih antara koordinat x: dx = x2
– x1. - Hitung selisih antara koordinat y: dy = y2
– y1.
Menghitung Kuadrat Selisih
- Kuadratkan selisih koordinat x: dx^2 = dx
– dx. - Kuadratkan selisih koordinat y: dy^2 = dy
– dy.
Menjumlahkan Kuadrat Selisih
Jumlahkan kuadrat selisih koordinat x dan y: d^2 = dx^2 + dy^2.
Mencari Akar Kuadrat
Terakhir, hitung akar kuadrat dari jumlah kuadrat selisih untuk mendapatkan jarak antara dua titik: d = √(d^2).
Aplikasi Jarak dalam Kehidupan Nyata

Konsep jarak memegang peranan penting dalam berbagai aspek kehidupan sehari-hari. Jarak digunakan untuk navigasi, konstruksi, perencanaan kota, dan banyak bidang lainnya.
Navigasi
Dalam navigasi, jarak digunakan untuk menentukan rute perjalanan, memperkirakan waktu tempuh, dan melacak kemajuan. Sistem GPS (Global Positioning System) menggunakan prinsip jarak untuk menentukan lokasi dan arah.
Konstruksi
Dalam konstruksi, jarak sangat penting untuk mengukur dan mengatur lokasi bangunan, struktur, dan infrastruktur lainnya. Jarak digunakan untuk memastikan bahwa struktur dibangun sesuai dengan rencana dan aman.
Perencanaan Kota
Dalam perencanaan kota, jarak digunakan untuk merencanakan tata letak kota, termasuk penempatan jalan, taman, dan fasilitas umum. Jarak membantu memastikan bahwa kota dapat diakses dan layak huni.
Ringkasan Akhir

Memahami konsep jarak antara dua titik sangat penting untuk berbagai aplikasi dalam kehidupan nyata. Dengan menggunakan rumus jarak, kita dapat memecahkan berbagai masalah geometri dan teknik, membantu kita menavigasi lingkungan kita secara akurat dan merencanakan struktur dengan tepat.
Bagian Pertanyaan Umum (FAQ)
Apa itu jarak antara dua titik?
Jarak antara dua titik pada bidang koordinat adalah panjang segmen garis yang menghubungkan kedua titik tersebut.
Bagaimana cara menghitung jarak antara dua titik?
Gunakan rumus jarak: jarak = √[(x2 – x1)² + (y2 – y1)²], di mana (x1, y1) dan (x2, y2) adalah koordinat kedua titik.
Apa saja aplikasi jarak dalam kehidupan nyata?
Aplikasi jarak meliputi navigasi (menghitung jarak antara dua lokasi), konstruksi (merencanakan tata letak bangunan), dan perencanaan kota (menentukan jarak antara fasilitas publik).