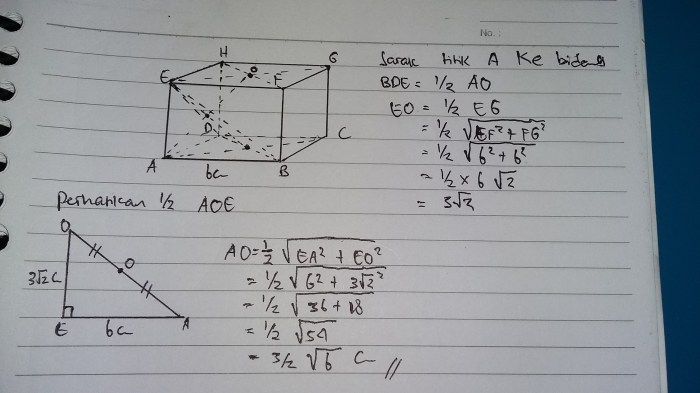
Dalam geometri, jarak titik ke bidang pada kubus merupakan konsep penting yang sering digunakan dalam berbagai aplikasi. Contoh soal jarak titik ke bidang pada kubus dapat membantu kita memahami konsep ini dengan lebih jelas.

Jarak titik ke bidang pada kubus adalah jarak antara sebuah titik di luar kubus dengan bidang yang terdapat di dalam kubus. Bidang ini bisa berupa salah satu sisi kubus atau bidang diagonal yang terbentuk oleh dua sisi kubus yang berdekatan.

Definisi Jarak Titik ke Bidang

Dalam geometri, jarak titik ke bidang pada kubus mengacu pada jarak antara titik tertentu dan bidang yang dibentuk oleh permukaan salah satu sisi kubus.

Untuk memperjelas konsep ini, bayangkan sebuah kubus dengan titik P berada di luar kubus. Jarak dari titik P ke bidang yang dibentuk oleh salah satu sisi kubus adalah jarak tegak lurus antara titik P dan bidang tersebut.

Rumus Jarak Titik ke Bidang

Rumus untuk menghitung jarak titik P(x ₁, y ₁, z ₁) ke bidang Ax + By + Cz + D = 0 adalah:

|Ax ₁+ By ₁+ Cz ₁+ D|/√(A ²+ B ²+ C ²)

di mana A, B, C adalah koefisien bidang, dan D adalah konstanta.

Contoh Soal

Misalkan sebuah kubus dengan panjang sisi 10 cm. Jika titik P berada di (12, 5, 7), hitung jarak dari titik P ke bidang yang dibentuk oleh sisi atas kubus.

Persamaan bidang atas kubus adalah z = 10.

Substitusikan nilai titik P dan persamaan bidang ke dalam rumus jarak:

|A(12) + B(5) + C(7) + D|/√(A ²+ B ²+ C ²)

Contoh soal jarak titik ke bidang pada kubus melibatkan perhitungan jarak antara titik dan bidang dalam ruang tiga dimensi. Untuk menyelesaikan soal semacam ini, diperlukan pemahaman konsep geometri analitik. Di sisi lain, “procedure text how to make a cup of coffee” menjelaskan langkah-langkah untuk menyeduh kopi dengan benar.

Meskipun berbeda topik, keduanya sama-sama menuntut pemahaman konsep yang jelas dan kemampuan berpikir analitis. Dalam contoh soal jarak titik ke bidang pada kubus, kita perlu memahami konsep jarak dan proyeksi, sedangkan pada procedure text how to make a cup of coffee, kita perlu memahami urutan langkah-langkah dan pengaruh bahan-bahan yang digunakan.

|120 + 50 + 70 + D|/√(1 + 1 + 1)

|240 + D|/√3

Karena bidang atas kubus terletak pada z = 10, maka D = -10.

Jadi, jarak dari titik P ke bidang atas kubus adalah:

|240 – 10|/√3 = 230/√3 cm

Rumus Jarak Titik ke Bidang

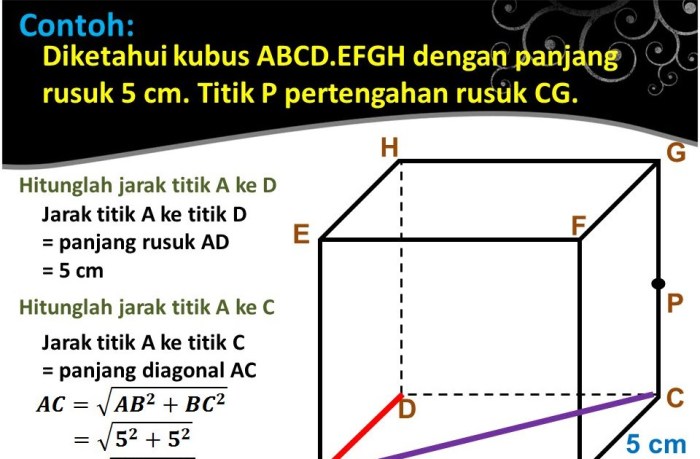
Dalam geometri, jarak titik ke bidang merupakan besaran yang mengukur seberapa jauh titik tersebut dari bidang. Pada kubus, terdapat enam bidang yang saling tegak lurus, dan rumus jarak titik ke bidang berbeda-beda tergantung pada bidang yang dimaksud.

Rumus Umum

Rumus umum untuk menghitung jarak titik Pke bidang dengan persamaan umum Ax+ By+ Cz+ D= 0 adalah:

d= | Ax₁+ By₁+ Cz₁+ D| / √( A²+ B²+ C²)

di mana:

• dadalah jarak titik Pke bidang
• x₁, y₁, z₁adalah koordinat titik P
• A, B, Cadalah koefisien dari persamaan bidang
• Dadalah konstanta dari persamaan bidang

Prosedur Menghitung Jarak Titik ke Bidang

Menghitung jarak titik ke bidang pada kubus memerlukan beberapa langkah sistematis. Prosedur berikut ini akan memandu Anda melalui proses tersebut:

Identifikasi Bidang dan Titik

Langkah pertama adalah mengidentifikasi bidang dan titik yang jaraknya ingin dihitung. Bidang pada kubus adalah permukaan datar yang dibatasi oleh empat sisi, sedangkan titik adalah lokasi tertentu dalam ruang tiga dimensi.

Tentukan Vektor Normal Bidang

Selanjutnya, tentukan vektor normal bidang. Vektor normal adalah vektor yang tegak lurus terhadap bidang. Untuk kubus, vektor normal dapat ditemukan dengan menghitung vektor silang dari dua vektor yang sejajar dengan sisi-sisi bidang.

Hitung Proyeksi Titik ke Bidang

Setelah vektor normal ditentukan, proyeksikan titik ke bidang. Proyeksi adalah titik pada bidang yang memiliki jarak terdekat dengan titik yang diberikan. Proyeksi dapat dihitung dengan mengalikan titik dengan vektor normal dan kemudian menormalkan hasilnya.

Dalam contoh soal jarak titik ke bidang pada kubus, kita dapat mengaplikasikan prinsip matematika dasar untuk menghitung jarak tersebut. Selain itu, pemahaman tentang rumus faktor pengenceran spektrofotometri juga dapat diterapkan dalam perhitungan konsentrasi zat dalam larutan. Dengan menggunakan prinsip spektrofotometri, kita dapat menentukan konsentrasi suatu zat dengan mengukur serapan cahaya pada panjang gelombang tertentu.

Dengan demikian, contoh soal jarak titik ke bidang pada kubus dan rumus faktor pengenceran spektrofotometri menjadi saling terkait dalam konteks penerapan prinsip matematika dan fisika dalam penyelesaian masalah.

Hitung Jarak, Contoh soal jarak titik ke bidang pada kubus

Terakhir, hitung jarak antara titik dan proyeksinya. Jarak ini sama dengan panjang vektor yang menghubungkan titik dan proyeksinya. Jarak dapat dihitung dengan menggunakan rumus jarak:

d = √[(x2

• x1)² + (y2
• y1)² + (z2
• z1)²]

di mana (x1, y1, z1) adalah koordinat titik dan (x2, y2, z2) adalah koordinat proyeksinya.

Contoh Soal dan Pembahasan Jarak Titik ke Bidang pada Kubus: Contoh Soal Jarak Titik Ke Bidang Pada Kubus

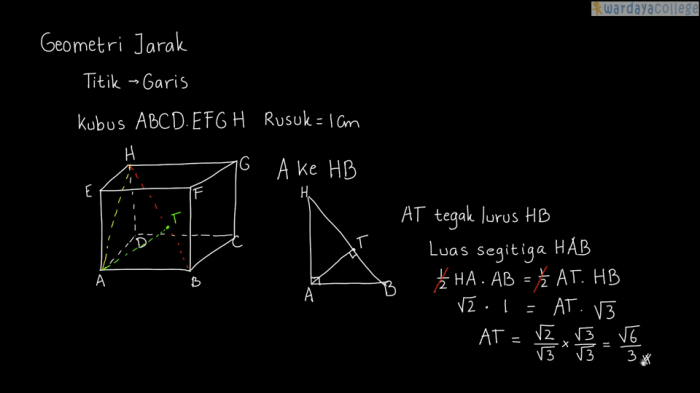
Jarak titik ke bidang pada kubus dapat dihitung menggunakan rumus:

d = |ax + by + cz + d| / √(a² + b² + c²)

di mana:

• (a, b, c) adalah vektor normal bidang
• d adalah konstanta bidang
• (x, y, z) adalah koordinat titik

Contoh Soal

Misalkan kita memiliki kubus dengan panjang rusuk 4 cm. Titik A berada di titik (2, 2, 2) dan bidang B memiliki persamaan x + y + z = 6. Hitung jarak dari titik A ke bidang B.

Penyelesaian

• Vektor normal bidang B adalah (1, 1, 1).
• Konstanta bidang B adalah
• 3. Ganti nilai vektor normal, konstanta bidang, dan koordinat titik A ke dalam rumus jarak:

“`d = |(1)(2) + (1)(2) + (1)(2) + 6| / √(1² + 1² + 1²)“`

4. Hitung nilai jarak

Dalam menentukan jarak titik ke bidang pada kubus, diperlukan pemahaman tentang koordinat titik dan persamaan bidang. Salah satu tugas penting dalam bidang telekomunikasi adalah peran telepon operator yang memiliki tugas dan tanggung jawab untuk mengelola dan menghubungkan panggilan telepon. Pemahaman tentang jarak titik ke bidang pada kubus sangat krusial dalam merancang sistem telekomunikasi yang efisien, karena jarak tersebut menentukan waktu tempuh sinyal antara perangkat komunikasi.

“`d = 10 / √3“`

Jadi, jarak dari titik A ke bidang B adalah 10 / √3 cm.

Aplikasi Jarak Titik ke Bidang

Rumus jarak titik ke bidang banyak digunakan dalam berbagai bidang kehidupan nyata, termasuk:

Arsitektur dan Desain Interior

Menghitung jarak antara titik tertentu dan bidang dinding atau langit-langit untuk penempatan perabotan, pencahayaan, atau elemen dekoratif.

Teknik Sipil

• Menentukan jarak antara permukaan jalan dan jembatan untuk memastikan jarak bebas yang aman.
• Menghitung jarak antara pondasi bangunan dan permukaan tanah untuk stabilitas struktural.

Fisika

Menghitung jarak antara titik tertentu dan bidang cermin atau lensa untuk menentukan sifat optik seperti pemantulan dan pembiasan cahaya.

Kedokteran

Menghitung jarak antara organ tubuh dan bidang tertentu untuk diagnosis dan perencanaan pengobatan, seperti jarak antara tumor dan kulit untuk terapi radiasi.

Komputer Grafis

Menghitung jarak antara titik dan bidang dalam model 3D untuk rendering yang akurat dan efek visual.

Kesimpulan

Memahami konsep jarak titik ke bidang pada kubus sangat penting karena memiliki berbagai aplikasi dalam kehidupan nyata, seperti dalam bidang arsitektur, desain interior, dan teknik mesin. Dengan memahami konsep ini, kita dapat memecahkan masalah yang melibatkan jarak antara titik dan bidang pada kubus secara efisien dan akurat.

Informasi FAQ

Apa yang dimaksud dengan jarak titik ke bidang pada kubus?

Jarak titik ke bidang pada kubus adalah jarak antara sebuah titik di luar kubus dengan bidang yang terdapat di dalam kubus.

Bagaimana cara menghitung jarak titik ke bidang pada kubus?

Dapat menggunakan rumus umum: jarak = |(a.b) – c| / |a|, di mana a adalah vektor normal bidang, b adalah vektor posisi titik, dan c adalah konstanta bidang.