Dalam fisika dan teknik, vektor memainkan peran penting dalam menggambarkan besaran yang memiliki baik besaran maupun arah. Komponen vektor adalah bagian-bagian penyusun vektor yang mewakili besar dan arahnya pada sumbu koordinat tertentu. Pemahaman tentang komponen vektor sangat penting untuk menyelesaikan berbagai masalah fisika dan teknik.

Artikel ini memberikan gambaran komprehensif tentang komponen vektor, termasuk definisi, jenis, operasi, dan aplikasinya. Selain itu, artikel ini menyajikan berbagai contoh soal yang umum digunakan untuk menguji pemahaman tentang topik ini, dilengkapi dengan tips dan trik untuk menyelesaikannya secara efektif.

Komponen Vektor

Dalam matematika, vektor adalah besaran yang memiliki besar dan arah. Vektor dapat direpresentasikan sebagai titik dalam ruang yang memiliki koordinat tertentu. Komponen vektor adalah koordinat-koordinat tersebut.

Contoh Vektor dan Komponennya

Misalkan kita memiliki vektor -*v yang dimulai dari titik (2, 3) dan berakhir di titik (5, 7). Komponen vektor -*v adalah:

• Komponen x: 5
  – 2 = 3
• Komponen y: 7
  – 3 = 4

Tabel Komponen Vektor yang Umum Digunakan

Nama Komponen	Notasi
Komponen x	vx
Komponen y	vy
Komponen z	vz

Operasi pada Komponen Vektor

Operasi pada komponen vektor melibatkan penjumlahan, pengurangan, dan perkalian dengan skalar. Operasi ini penting untuk manipulasi dan analisis vektor.

Penjumlahan dan Pengurangan

Penjumlahan dan pengurangan vektor dilakukan dengan menambahkan atau mengurangi komponen yang sesuai. Jika kita memiliki dua vektor a = (a ₁ , a ₂ , a ₃ ) dan b = (b ₁ , b ₂ , b ₃ ), maka:

• a + b = (a₁ + b₁, a₂ + b₂, a₃ + b₃)
• a
  – b = (a₁
  – b₁, a₂
  – b₂, a₃
  – b₃)

Perkalian dengan Skalar

Perkalian vektor dengan skalar k dilakukan dengan mengalikan setiap komponen vektor dengan k . Jika kita memiliki vektor a = (a ₁ , a ₂ , a ₃ ), maka:

• ka = (ka₁, ka₂, ka₃)

Flowchart Operasi Vektor

Flowchart berikut menunjukkan langkah-langkah untuk melakukan operasi penjumlahan, pengurangan, dan perkalian skalar pada komponen vektor:

1. Tentukan vektor a dan b atau skalar k.
2. Lakukan operasi yang sesuai pada komponen vektor (penjumlahan, pengurangan, atau perkalian).
3. Hasilnya adalah vektor baru atau vektor yang dimodifikasi.

Aplikasi Komponen Vektor

Komponen vektor memiliki banyak aplikasi dalam berbagai bidang, termasuk fisika, teknik, dan kedokteran. Komponen vektor memungkinkan kita untuk menguraikan besaran vektor menjadi komponen-komponennya yang lebih sederhana, yang membuatnya lebih mudah untuk memahami dan menganalisis besaran tersebut.

Aplikasi dalam Fisika

Dalam fisika, komponen vektor digunakan untuk menguraikan besaran-besaran vektor seperti kecepatan, perpindahan, dan gaya. Misalnya, kecepatan suatu benda dapat diuraikan menjadi komponen-komponennya pada sumbu x, y, dan z. Hal ini memungkinkan kita untuk memahami arah dan besaran kecepatan benda dalam tiga dimensi.

Aplikasi dalam Industri

• Teknik: Komponen vektor digunakan dalam teknik untuk menganalisis gaya dan tekanan pada struktur, merancang mesin, dan mengoptimalkan proses manufaktur.
• Kedokteran: Komponen vektor digunakan dalam kedokteran untuk menganalisis gerakan pasien, merencanakan operasi, dan mengembangkan perangkat medis.

Aplikasi dalam Pengolahan Citra

Dalam pengolahan citra, komponen vektor digunakan untuk menganalisis dan memanipulasi gambar. Misalnya, komponen vektor dapat digunakan untuk mendeteksi tepi, menghilangkan noise, dan mengenali objek dalam suatu gambar.

Contoh Soal Komponen Vektor

Dalam fisika dan matematika, komponen vektor memainkan peran penting dalam menyelesaikan masalah yang melibatkan besaran vektor. Soal komponen vektor umumnya menguji kemampuan siswa untuk menguraikan vektor menjadi komponen-komponennya, melakukan operasi pada komponen-komponen tersebut, dan kemudian menyusun kembali vektor yang dihasilkan.

Jenis Soal Komponen Vektor

Beberapa jenis soal komponen vektor yang umum meliputi:

• Mengidentifikasi komponen-komponen vektor dalam arah sumbu koordinat.
• Menghitung besar dan arah vektor dari komponen-komponennya.
• Menjumlahkan, mengurangkan, dan mengalikan vektor berdasarkan komponen-komponennya.
• Menentukan proyeksi vektor pada sumbu koordinat.
• Mencari sudut antara dua vektor menggunakan komponen-komponennya.

Contoh Soal

1. Sebuah vektor memiliki komponen (3, 4). Tentukan besar dan arah vektor tersebut.
2. Dua vektor, A = (2,1) dan B = (3, 5), dijumlahkan. Tentukan vektor yang dihasilkan.
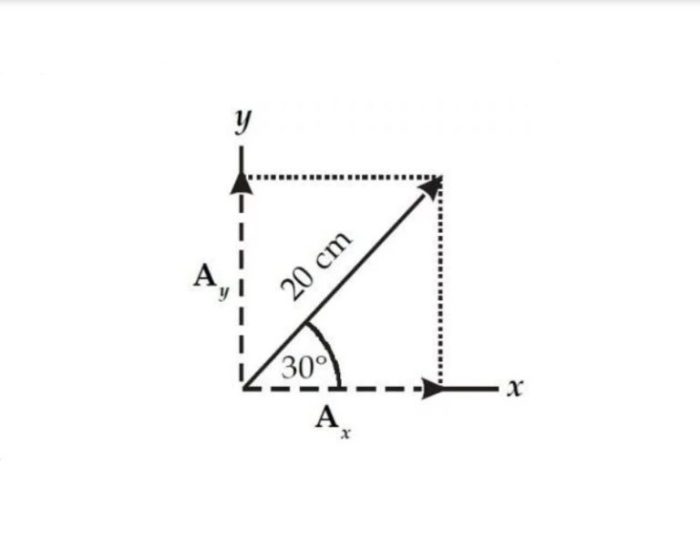
3. Sebuah vektor memiliki besar 10 dan membentuk sudut 30° dengan sumbu x positif. Tentukan komponen-komponen vektor tersebut.
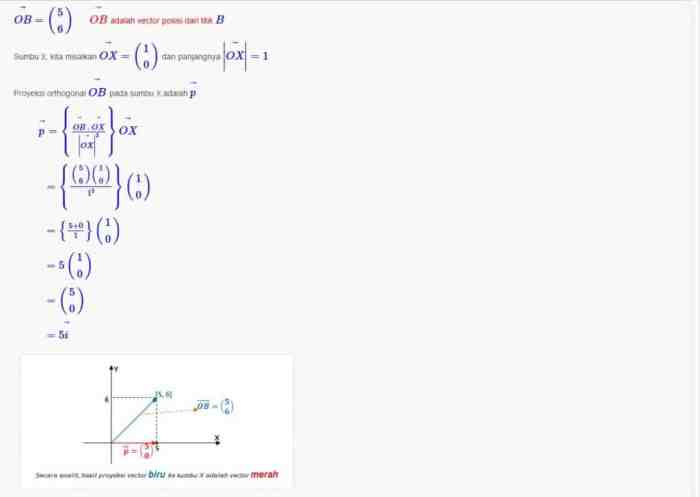
4. Sebuah vektor diproyeksikan pada sumbu y menghasilkan panjang proyeksi 5. Jika besar vektor adalah 13, tentukan sudut antara vektor dan sumbu y.

Tips dan Trik

Berikut adalah beberapa tips dan trik untuk menyelesaikan soal komponen vektor:

• Visualisasikan vektor menggunakan diagram untuk memudahkan pemahaman.
• Gunakan aturan segitiga dan Pythagoras untuk menentukan besar dan arah vektor.
• Terapkan rumus operasi vektor (penjumlahan, pengurangan, perkalian) pada komponen-komponennya.
• Gunakan fungsi trigonometri untuk menentukan proyeksi dan sudut vektor.

Penutupan

Komponen vektor adalah alat yang ampuh untuk menganalisis dan menyelesaikan masalah dalam berbagai bidang. Pemahaman yang kuat tentang komponen vektor memungkinkan individu untuk menguasai konsep fisika dan teknik yang kompleks dan menerapkannya dalam berbagai aplikasi dunia nyata. Artikel ini memberikan dasar yang komprehensif untuk topik ini, melengkapi pembaca dengan pengetahuan dan keterampilan yang diperlukan untuk unggul dalam bidang yang membutuhkan pemahaman tentang komponen vektor.

Pertanyaan dan Jawaban

Apa perbedaan antara vektor dan komponen vektor?

Vektor adalah besaran yang memiliki baik besaran maupun arah, sedangkan komponen vektor adalah besaran skalar yang mewakili besar vektor pada sumbu koordinat tertentu.

Bagaimana cara menemukan komponen vektor?

Komponen vektor dapat ditemukan dengan memproyeksikan vektor ke sumbu koordinat yang diinginkan dan mengukur panjang proyeksi.

Apa saja jenis-jenis operasi vektor yang umum?

Operasi vektor yang umum meliputi penjumlahan, pengurangan, perkalian skalar, dan perkalian vektor.

Bagaimana cara menyelesaikan soal komponen vektor?

Untuk menyelesaikan soal komponen vektor, pecahkan vektor menjadi komponennya, lakukan operasi pada komponen tersebut, lalu gabungkan hasilnya untuk mendapatkan vektor resultan.