Dalam matematika, koordinat Kartesius memainkan peran penting dalam menentukan lokasi titik pada bidang datar. Sistem ini menggunakan pasangan bilangan untuk merepresentasikan posisi titik, yang membuka berbagai aplikasi dalam kehidupan sehari-hari.
Panduan ini akan mengulas konsep koordinat Kartesius, mengidentifikasi kuadran pada bidang Kartesius, mengeksplorasi operasi dasar pada koordinat, dan menyajikan contoh soal beserta pembahasannya untuk pemahaman yang lebih mendalam.
Pengertian Koordinat Kartesius
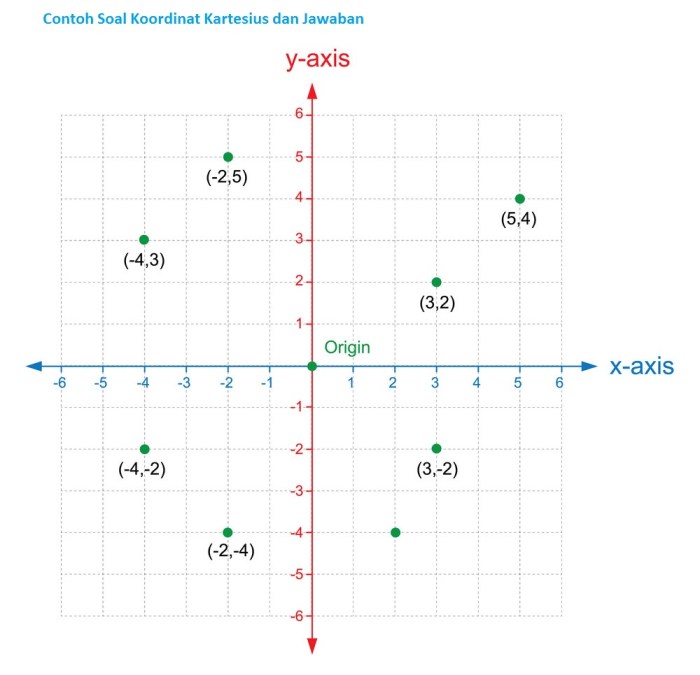
Koordinat Kartesius adalah sistem koordinat yang digunakan untuk menentukan lokasi titik pada bidang datar. Sistem ini diciptakan oleh matematikawan Prancis René Descartes pada abad ke-17.
Pada bidang Kartesius, setiap titik ditentukan oleh dua bilangan, yaitu absis dan ordinat. Absis (x) adalah jarak horizontal dari titik ke sumbu vertikal, sedangkan ordinat (y) adalah jarak vertikal dari titik ke sumbu horizontal.
Pasangan Bilangan
- Titik pada bidang Kartesius dinyatakan sebagai pasangan bilangan (x, y).
- Misalnya, titik (3, 5) menunjukkan titik yang terletak 3 satuan ke kanan dari sumbu vertikal dan 5 satuan ke atas dari sumbu horizontal.
Lokasi Titik
- Lokasi titik pada bidang Kartesius dapat ditentukan dengan menggunakan pasangan bilangannya.
- Untuk menentukan lokasi titik (3, 5), hitung 3 satuan ke kanan dari sumbu vertikal dan 5 satuan ke atas dari sumbu horizontal.
- Titik yang terletak pada perpotongan sumbu vertikal dan sumbu horizontal adalah titik asal (0, 0).
Kuadran pada Bidang Kartesius
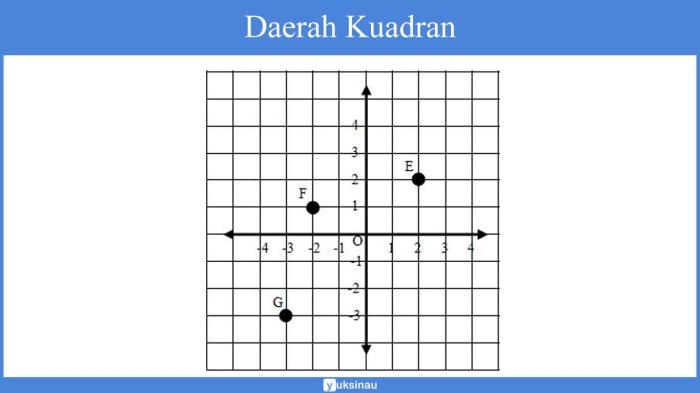
Bidang Kartesius dibagi menjadi empat kuadran, yang masing-masing memiliki tanda koordinat (x,y) yang berbeda.
Identifikasi Kuadran
Berikut adalah identifikasi empat kuadran pada bidang Kartesius beserta batasannya:
- Kuadran I: x > 0 dan y > 0
- Kuadran II: x < 0 dan y > 0
- Kuadran III: x < 0 dan y < 0
- Kuadran IV: x > 0 dan y < 0
Contoh Titik di Setiap Kuadran
Berikut adalah contoh titik yang terletak di setiap kuadran:
- Kuadran I: (2, 3)
- Kuadran II: (-2, 3)
- Kuadran III: (-2,
-3) - Kuadran IV: (2,
-3)
Operasi pada Koordinat Kartesius

Dalam koordinat Kartesius, operasi penjumlahan dan pengurangan dapat dilakukan pada koordinat titik-titiknya. Operasi ini menghasilkan titik baru yang merupakan hasil operasi tersebut.
Penjumlahan Koordinat
Untuk menjumlahkan dua titik (x1, y1) dan (x2, y2), koordinat x dan y dijumlahkan secara terpisah. Hasilnya adalah titik baru (x3, y3) dengan koordinat:
x3 = x1 + x2y3 = y1 + y2
Sebagai contoh, jika kita menjumlahkan titik (3, 5) dan (2, 4), kita akan mendapatkan titik baru (5, 9).
Pengurangan Koordinat
Untuk mengurangkan titik (x1, y1) dengan titik (x2, y2), koordinat x dan y dikurangkan secara terpisah. Hasilnya adalah titik baru (x3, y3) dengan koordinat:
x3 = x1
x2
y3 = y1
y2
Sebagai contoh, jika kita mengurangkan titik (5, 9) dengan titik (2, 4), kita akan mendapatkan titik baru (3, 5).
Aplikasi Koordinat Kartesius dalam Kehidupan Sehari-hari
Koordinat Kartesius memainkan peran penting dalam berbagai aspek kehidupan kita. Ini adalah sistem koordinat yang menggunakan dua garis bilangan tegak lurus, yang disebut sumbu x dan y, untuk menentukan lokasi suatu titik dalam bidang dua dimensi.
Membuat Peta
Koordinat Kartesius banyak digunakan dalam pembuatan peta. Setiap lokasi di peta dapat ditentukan oleh koordinat x dan y-nya. Koordinat x menunjukkan jarak horizontal dari titik asal, sedangkan koordinat y menunjukkan jarak vertikal.
Sebagai contoh, pertimbangkan sebuah peta kota. Titik asal dapat dipilih sebagai persimpangan jalan utama. Lokasi sebuah rumah dapat ditentukan dengan memberikan koordinat x dan y-nya relatif terhadap titik asal ini.
Menentukan Arah
Koordinat Kartesius juga digunakan dalam menentukan arah. Misalnya, dalam navigasi, koordinat Kartesius digunakan untuk menentukan posisi kapal atau pesawat. Koordinat ini dapat digunakan untuk menghitung arah dan jarak ke tujuan.
Selain itu, koordinat Kartesius juga digunakan dalam berbagai bidang lain, seperti arsitektur, teknik, dan kedokteran. Dalam arsitektur, koordinat Kartesius digunakan untuk mendesain bangunan dan menentukan lokasi ruangan. Dalam teknik, koordinat Kartesius digunakan untuk merancang mesin dan struktur. Dalam kedokteran, koordinat Kartesius digunakan untuk menentukan lokasi organ dan tumor dalam tubuh.
Contoh Soal dan Pembahasan Koordinat Kartesius Kelas 8

Koordinat Kartesius adalah sistem untuk menentukan lokasi titik pada bidang datar menggunakan dua bilangan, yang disebut koordinat x dan y. Berikut beberapa contoh soal koordinat Kartesius kelas 8 beserta langkah-langkah penyelesaian dan jawabannya:
Soal 1
Tentukan koordinat titik yang terletak 3 satuan ke kanan dan 2 satuan ke atas dari titik (2, 5).
Langkah-langkah penyelesaian:
- Gerak ke kanan 3 satuan: x = 2 + 3 = 5
- Gerak ke atas 2 satuan: y = 5 + 2 = 7
Jawaban: (5, 7)
Soal 2
Sebuah persegi panjang memiliki panjang 6 satuan dan lebar 4 satuan. Tentukan koordinat titik sudut-sudut persegi panjang tersebut jika salah satu titik sudutnya adalah (2, 3).
Langkah-langkah penyelesaian:
- Sudut kanan atas: (2 + 6, 3 + 4) = (8, 7)
- Sudut kiri bawah: (2, 3
– 4) = (2,
-1) - Sudut kanan bawah: (2 + 6, 3
– 4) = (8,
-1) - Sudut kiri atas: (2, 3 + 4) = (2, 7)
Jawaban: (2, 3), (8, 7), (2, -1), (8, -1)
Soal 3
Tentukan jarak antara titik A(-2, 3) dan B(4, 1).
Langkah-langkah penyelesaian:
- Selisih koordinat x: 4
(-2) = 6
- Selisih koordinat y: 1
- 3 =
- 2
- Kuadratkan selisih koordinat x dan y: 6² = 36 dan (-2)² = 4
- Jumlahkan hasil kuadrat: 36 + 4 = 40
- Ambil akar kuadrat dari hasil penjumlahan: √40 = 2√10
Jawaban: 2√10 satuan
Kesimpulan
Memahami koordinat Kartesius tidak hanya penting untuk kemajuan dalam matematika, tetapi juga memiliki aplikasi luas dalam bidang seperti navigasi, pemetaan, dan ilmu komputer. Dengan menguasai konsep ini, siswa dapat membangun dasar yang kuat untuk pemecahan masalah dan eksplorasi matematika yang lebih lanjut.
Jawaban untuk Pertanyaan Umum
Apa saja langkah-langkah untuk menentukan kuadran suatu titik?
Periksa tanda kedua koordinat titik. Jika keduanya positif, titik tersebut berada di kuadran I; jika koordinat x positif dan koordinat y negatif, titik tersebut berada di kuadran IV; jika koordinat x negatif dan koordinat y positif, titik tersebut berada di kuadran II; jika kedua koordinat negatif, titik tersebut berada di kuadran III.
Bagaimana cara menjumlahkan dua titik pada bidang Kartesius?
Tambahkan koordinat x dari kedua titik untuk mendapatkan koordinat x dari titik baru, dan tambahkan koordinat y dari kedua titik untuk mendapatkan koordinat y dari titik baru.
Dalam kehidupan nyata, apa saja contoh penerapan koordinat Kartesius?
Koordinat Kartesius digunakan dalam sistem GPS, pemetaan, dan perencanaan kota untuk menentukan lokasi dan merencanakan rute.
