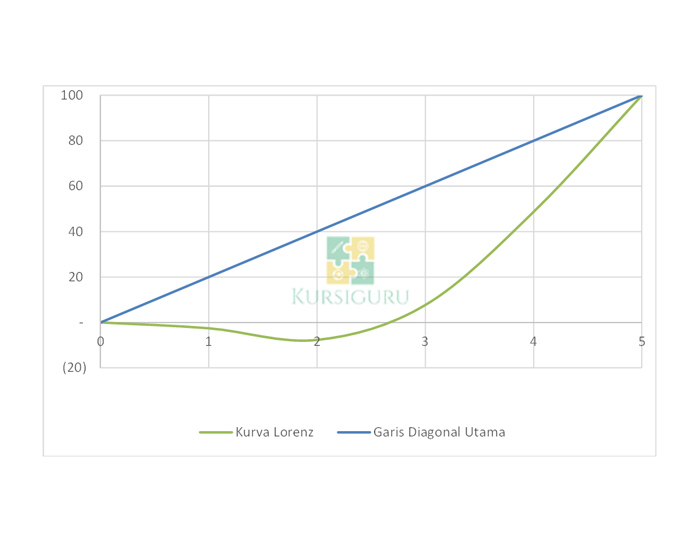
Kurva Lorenz merupakan alat penting untuk mengukur kesenjangan pendapatan dalam suatu masyarakat. Kurva ini menunjukkan distribusi pendapatan kumulatif suatu populasi, sehingga memberikan gambaran visual tentang seberapa merata pendapatan didistribusikan.
Penggunaan Kurva Lorenz sangat luas, mulai dari analisis kesenjangan ekonomi hingga evaluasi kebijakan publik yang bertujuan mengurangi ketidaksetaraan.
Konsep Kurva Lorenz
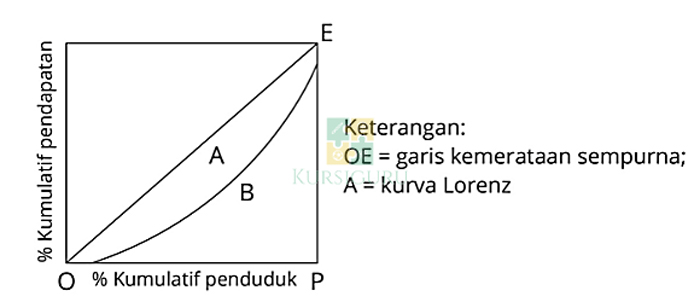
Kurva Lorenz adalah alat grafis yang digunakan untuk mengukur kesenjangan pendapatan dalam suatu populasi. Kurva ini menunjukkan distribusi pendapatan kumulatif, di mana persentase populasi terbawah diplot pada sumbu horizontal, dan persentase pendapatan kumulatif diplot pada sumbu vertikal.
Kurva Lorenz yang lebih curam menunjukkan kesenjangan pendapatan yang lebih tinggi, karena menunjukkan bahwa sebagian besar pendapatan terkonsentrasi di tangan sebagian kecil populasi. Sebaliknya, kurva Lorenz yang lebih datar menunjukkan kesenjangan pendapatan yang lebih rendah, karena menunjukkan bahwa pendapatan didistribusikan lebih merata di seluruh populasi.
Contoh Praktis
- Dalam praktiknya, Kurva Lorenz dapat digunakan untuk membandingkan kesenjangan pendapatan antara negara-negara yang berbeda.
- Kurva Lorenz juga dapat digunakan untuk memantau tren kesenjangan pendapatan dari waktu ke waktu dalam suatu negara.
- Selain itu, Kurva Lorenz dapat digunakan untuk menilai efektivitas kebijakan pemerintah yang bertujuan untuk mengurangi kesenjangan pendapatan.
Contoh Soal Kurva Lorenz
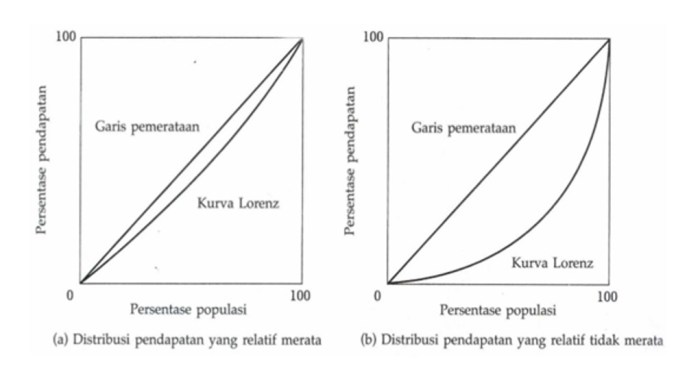
Berikut adalah beberapa contoh soal Kurva Lorenz, beserta data dan langkah-langkah penyelesaiannya:
Contoh Soal 1
Data distribusi pendapatan dalam suatu negara adalah sebagai berikut:
- 10% terbawah: Rp 10.000.000
- 20% kedua: Rp 20.000.000
- 30% ketiga: Rp 30.000.000
- 40% keempat: Rp 40.000.000
- 10% teratas: Rp 50.000.000
Tentukan koefisien Gini dari distribusi pendapatan tersebut dan gambar Kurva Lorenznya.
Langkah-langkah Penyelesaian:
- Hitung persentase kumulatif pendapatan untuk setiap kelompok:
- 10% terbawah: 10%
- 20% kedua: 30%
- 30% ketiga: 60%
- 40% keempat: 100%
- 10% teratas: 100%
- Hitung persentase kumulatif penduduk untuk setiap kelompok:
- 10% terbawah: 10%
- 20% kedua: 30%
- 30% ketiga: 60%
- 40% keempat: 100%
- 10% teratas: 100%
- Plot persentase kumulatif pendapatan terhadap persentase kumulatif penduduk untuk mendapatkan Kurva Lorenz.
- Hitung koefisien Gini menggunakan rumus:
- Di mana luas di bawah garis diagonal adalah 0,5 dan luas di bawah Kurva Lorenz dapat dihitung menggunakan integral atau pendekatan numerik.
Gini = 2 x (Luas di bawah garis diagonal
Luas di bawah Kurva Lorenz) / Luas di bawah garis diagonal
Contoh Soal 2
Dua negara, A dan B, memiliki distribusi pendapatan yang berbeda. Negara A memiliki koefisien Gini sebesar 0,4, sedangkan negara B memiliki koefisien Gini sebesar 0,6. Jelaskan perbedaan tingkat kesenjangan pendapatan antara kedua negara berdasarkan koefisien Gini tersebut.
Langkah-langkah Penyelesaian:
- Koefisien Gini yang lebih tinggi menunjukkan kesenjangan pendapatan yang lebih besar.
- Oleh karena itu, negara B memiliki kesenjangan pendapatan yang lebih besar dibandingkan dengan negara A.
- Hal ini berarti bahwa distribusi pendapatan di negara B lebih tidak merata, dengan sebagian kecil penduduk memiliki pendapatan yang jauh lebih tinggi daripada sebagian besar penduduk lainnya.
Cara Menggambar Kurva Lorenz
Kurva Lorenz adalah representasi grafis dari distribusi pendapatan atau kekayaan dalam suatu populasi. Menggambar Kurva Lorenz memerlukan langkah-langkah berikut:
Langkah-langkah Menggambar Kurva Lorenz
- Urutkan data: Urutkan data pendapatan atau kekayaan dari yang terendah hingga tertinggi.
- Hitung persentase kumulatif: Hitung persentase kumulatif pendapatan atau kekayaan untuk setiap titik data.
- Hitung persentase kumulatif populasi: Hitung persentase kumulatif populasi untuk setiap titik data.
- Plot titik: Plot titik pada grafik dengan persentase kumulatif populasi pada sumbu x dan persentase kumulatif pendapatan atau kekayaan pada sumbu y.
- Hubungkan titik: Hubungkan titik-titik tersebut dengan garis untuk membentuk Kurva Lorenz.
Ilustrasi
Berikut adalah ilustrasi cara menggambar Kurva Lorenz:
- Urutkan data: [10, 20, 30, 40, 50]
- Hitung persentase kumulatif pendapatan: [2%, 6%, 12%, 20%, 30%]
- Hitung persentase kumulatif populasi: [20%, 40%, 60%, 80%, 100%]
- Plot titik: (20%, 2%), (40%, 6%), (60%, 12%), (80%, 20%), (100%, 30%)
- Hubungkan titik: Hubungkan titik-titik tersebut untuk membentuk Kurva Lorenz.
Interpretasi Kurva Lorenz
Kurva Lorenz adalah alat grafis yang digunakan untuk menggambarkan distribusi pendapatan dalam suatu masyarakat. Ini membantu memahami tingkat kesenjangan pendapatan dengan membandingkan persentase pendapatan kumulatif dengan persentase populasi kumulatif.
Kurva Lorenz yang mendekati garis diagonal sempurna menunjukkan distribusi pendapatan yang merata. Sebaliknya, kurva yang jauh dari garis diagonal menunjukkan kesenjangan pendapatan yang tinggi, di mana sebagian kecil populasi menguasai sebagian besar pendapatan.
Koefisien Gini
Koefisien Gini adalah ukuran statistik yang digunakan untuk mengevaluasi kesenjangan pendapatan berdasarkan Kurva Lorenz. Ini dihitung sebagai rasio antara luas area di bawah garis diagonal sempurna dan luas total di bawah Kurva Lorenz.
Koefisien Gini berkisar dari 0 hingga 1. Nilai 0 menunjukkan distribusi pendapatan yang sempurna, sedangkan nilai 1 menunjukkan kesenjangan pendapatan yang sempurna. Semakin tinggi koefisien Gini, semakin tinggi kesenjangan pendapatan.
Aplikasi Kurva Lorenz

Kurva Lorenz memiliki aplikasi luas dalam berbagai bidang, termasuk ekonomi, kebijakan publik, dan studi pembangunan. Kurva ini digunakan untuk menganalisis kesenjangan pendapatan dan kekayaan dalam suatu masyarakat, dan untuk mengevaluasi efektivitas kebijakan yang dirancang untuk mengurangi kesenjangan.
Aplikasi dalam Ekonomi
- Menganalisis distribusi pendapatan dan kekayaan dalam suatu negara atau wilayah.
- Membandingkan kesenjangan pendapatan antar negara atau wilayah.
- Mengevaluasi dampak kebijakan ekonomi, seperti pajak progresif dan jaring pengaman sosial, pada kesenjangan.
Aplikasi dalam Kebijakan Publik
- Memandu pengambilan keputusan kebijakan mengenai program sosial dan ekonomi.
- Menetapkan tujuan kebijakan untuk mengurangi kesenjangan dan meningkatkan pemerataan.
- Mengevaluasi efektivitas program kebijakan dalam mengurangi kesenjangan.
Aplikasi dalam Studi Pembangunan
- Menganalisis kesenjangan pendapatan dan kekayaan di negara berkembang.
- Membandingkan kesenjangan pembangunan antar negara.
- Mengevaluasi dampak program pembangunan pada kesenjangan.
Ringkasan Penutup
Memahami cara menggambar dan menafsirkan Kurva Lorenz sangat penting untuk menganalisis kesenjangan pendapatan dan mengembangkan kebijakan yang efektif untuk mempromosikan distribusi pendapatan yang lebih adil.
Sudut Pertanyaan Umum (FAQ)
Apa itu koefisien Gini?
Koefisien Gini adalah ukuran numerik kesenjangan pendapatan yang berkisar antara 0 hingga 1. Nilai 0 menunjukkan distribusi pendapatan yang sempurna, sedangkan nilai 1 menunjukkan kesenjangan pendapatan yang sempurna.
Bagaimana cara menggambar Kurva Lorenz?
Untuk menggambar Kurva Lorenz, pertama-tama urutkan populasi dari pendapatan terendah hingga tertinggi. Kemudian, hitung persentase kumulatif pendapatan dan populasi. Terakhir, plot persentase kumulatif pendapatan pada sumbu y dan persentase kumulatif populasi pada sumbu x.
Apa saja aplikasi Kurva Lorenz?
Kurva Lorenz memiliki berbagai aplikasi, termasuk mengidentifikasi daerah dengan kesenjangan pendapatan yang tinggi, mengevaluasi efektivitas program pengentasan kemiskinan, dan menganalisis tren kesenjangan pendapatan dari waktu ke waktu.