Dalam geometri, lingkaran dalam segitiga memegang peran penting sebagai bentuk geometri yang bersinggungan dengan tiga sisi segitiga. Lingkaran ini memberikan wawasan yang berharga tentang sifat-sifat segitiga dan memiliki berbagai aplikasi dalam pemecahan masalah.
Dalam artikel ini, kita akan membahas konsep dasar lingkaran dalam segitiga, rumus untuk menghitung jari-jarinya, sifat-sifatnya yang unik, dan penerapannya dalam geometri dan pemecahan masalah. Selain itu, kami akan memberikan contoh soal untuk memperjelas konsep ini dan menunjukkan penerapan praktisnya.
Pengertian Lingkaran dalam Segitiga
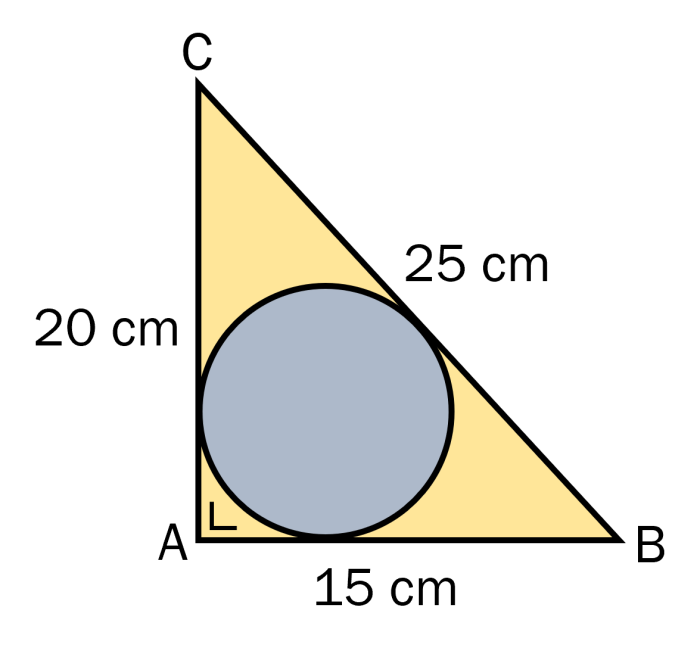
Dalam geometri, lingkaran dalam segitiga adalah lingkaran terbesar yang dapat digambar di dalam segitiga dan bersinggungan dengan ketiga sisi segitiga tersebut.
Ilustrasi
Berikut adalah ilustrasi lingkaran dalam segitiga:
Pusat lingkaran dalam segitiga terletak pada titik perpotongan garis-garis bagi dari sudut-sudut segitiga.
Rumus Lingkaran dalam Segitiga

Lingkaran dalam segitiga adalah lingkaran yang bersinggungan dengan ketiga sisi segitiga. Jari-jari lingkaran dalam segitiga dapat dihitung menggunakan rumus berikut:$$r = \fracAs$$di mana:* $$r$$ adalah jari-jari lingkaran dalam
- $$A$$ adalah luas segitiga
- $$s$$ adalah setengah keliling segitiga
Contoh Soal
Hitunglah jari-jari lingkaran dalam segitiga dengan panjang sisi 6 cm, 8 cm, dan 10 cm. Solusi:
1. Hitung setengah keliling segitiga
$$s = \frac6 + 8 + 102 = 12$$
2. Hitung luas segitiga menggunakan rumus Heron
$$A = \sqrts(s-a)(s-b)(s-c) = \sqrt12(12-6)(12-8)(12-10) = 24$$
3. Hitung jari-jari lingkaran dalam
$$r = \fracAs = \frac2412 = 2$$Jadi, jari-jari lingkaran dalam segitiga tersebut adalah 2 cm.
Sifat-sifat Lingkaran dalam Segitiga
Lingkaran dalam segitiga adalah lingkaran terbesar yang dapat digambar di dalam segitiga dan menyinggung ketiga sisi segitiga tersebut. Titik pusat lingkaran dalam disebut incenter.
Titik Pusat Lingkaran Dalam
Incenter segitiga adalah titik potong dari tiga garis bagi dalam segitiga tersebut. Garis bagi dalam adalah garis yang membagi sisi segitiga menjadi dua bagian yang sama panjang.
Titik Singgung
Titik singgung lingkaran dalam dengan sisi segitiga disebut titik singgung. Terdapat tiga titik singgung pada lingkaran dalam segitiga, yaitu satu titik singgung pada setiap sisi segitiga.
Hubungan dengan Sifat Segitiga
- Jari-jari Lingkaran Dalam: Jari-jari lingkaran dalam berbanding lurus dengan luas segitiga dan berbanding terbalik dengan setengah keliling segitiga.
- Panjang Sisi Segitiga: Panjang sisi segitiga berbanding lurus dengan tangen setengah sudut yang berhadapan dengan sisi tersebut dan jari-jari lingkaran dalam.
- Luas Segitiga: Luas segitiga berbanding lurus dengan setengah keliling segitiga dan jari-jari lingkaran dalam.
Penerapan Lingkaran dalam Segitiga

Lingkaran dalam segitiga memiliki penerapan yang luas dalam geometri dan pemecahan masalah. Lingkaran ini membantu menentukan sifat-sifat segitiga dan memberikan wawasan tentang hubungan antar sisi dan sudutnya.
Contoh Soal
Misalkan kita memiliki segitiga ABC dengan panjang sisi AB = 8 cm, BC = 10 cm, dan CA = 12 cm. Hitunglah jari-jari lingkaran dalam segitiga tersebut.
- Mencari Semiperimeter Segitiga:
s = (AB + BC + CA) / 2 = (8 + 10 + 12) / 2 = 15 cm
- Mencari Jari-jari Lingkaran Dalam:
r = s / (s – AB) / (s – BC) / (s – CA) = 15 / (15 – 8) / (15 – 10) / (15 – 12) = 3 cm
Teorema Lingkaran dalam Segitiga
Lingkaran dalam segitiga adalah lingkaran terbesar yang dapat digambar di dalam segitiga, dan menyinggung ketiga sisi segitiga. Lingkaran dalam segitiga memiliki sifat-sifat khusus yang dijelaskan dalam teorema-teorema berikut:
Teorema Apollonius
Teorema Apollonius menyatakan bahwa jika lingkaran dalam segitiga menyinggung sisi-sisi segitiga pada titik-titik A, B, dan C, maka:
- Panjang jari-jari lingkaran dalam (r) adalah:
r = (s – a)(s – b)(s – c) / s
di mana s adalah setengah keliling segitiga dan a, b, c adalah panjang sisi-sisi segitiga.
- Jari-jari lingkaran dalam berbanding terbalik dengan jumlah sisi-sisi segitiga:
- r : (a + b + c) = 1 : 4R
- Luas lingkaran dalam berbanding lurus dengan luas segitiga:
- Luas lingkaran : Luas segitiga = 1 : 4
Penutupan

Memahami konsep lingkaran dalam segitiga sangat penting untuk mengembangkan keterampilan berpikir spasial dan geometrik. Rumus, sifat, dan penerapannya memberikan dasar yang kuat untuk memecahkan masalah kompleks dan mengungkap hubungan tersembunyi dalam bentuk geometri. Dengan menguasai konsep ini, individu dapat mengembangkan apresiasi yang lebih dalam terhadap keindahan dan kegunaan matematika.
Pertanyaan Umum yang Sering Muncul
Apa itu lingkaran dalam segitiga?
Lingkaran dalam segitiga adalah lingkaran terbesar yang dapat digambar di dalam segitiga, bersinggungan dengan ketiga sisi segitiga.
Bagaimana cara menghitung jari-jari lingkaran dalam segitiga?
Jari-jari lingkaran dalam segitiga dapat dihitung menggunakan rumus: r = (s – a)(s – b)(s – c)/s, di mana s adalah setengah keliling segitiga dan a, b, c adalah panjang sisi-sisinya.
Apa saja sifat-sifat lingkaran dalam segitiga?
Lingkaran dalam segitiga memiliki sifat-sifat unik, seperti titik pusatnya yang selalu terletak di titik perpotongan garis bagi dalam segitiga dan titik singgungnya yang selalu terletak di titik tengah sisi-sisi segitiga.
Bagaimana lingkaran dalam segitiga digunakan dalam geometri?
Lingkaran dalam segitiga digunakan untuk membuktikan teorema dan sifat-sifat segitiga, seperti Teorema Apollonius dan Teorema Heron.
Apa saja contoh penerapan lingkaran dalam segitiga dalam kehidupan nyata?
Lingkaran dalam segitiga memiliki penerapan dalam berbagai bidang, seperti desain arsitektur, teknik sipil, dan robotika.