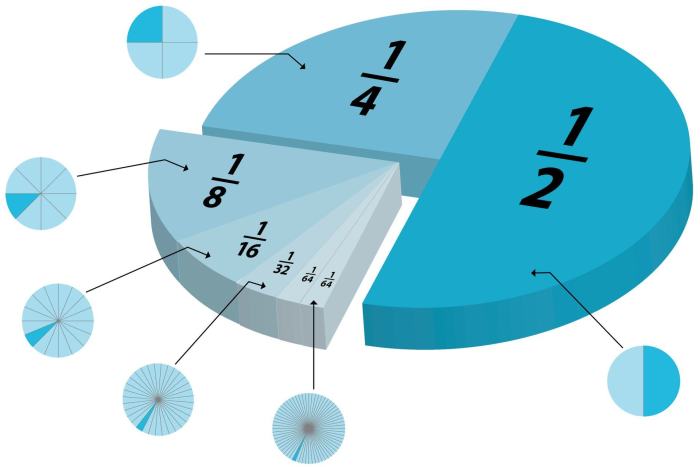
Pecahan merupakan konsep penting dalam matematika yang merepresentasikan bagian dari keseluruhan. Memahami pecahan sangat penting untuk berbagai aplikasi dalam kehidupan sehari-hari, seperti memasak, keuangan, dan pembagian tugas.
Dalam panduan ini, kita akan menjelajahi dasar-dasar pecahan, termasuk konsep, operasi, dan penyederhanaan. Kita juga akan menyediakan daftar contoh soal pecahan dan jawabannya untuk membantu Anda menguasai topik ini.
Operasi Dasar Pecahan
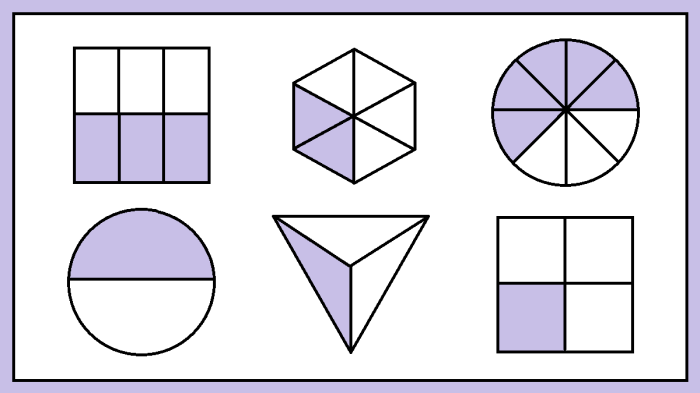
Pecahan adalah bilangan yang menyatakan bagian dari suatu keseluruhan. Operasi dasar pecahan meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan dan Pengurangan Pecahan
Untuk menjumlahkan atau mengurangkan pecahan, penyebutnya harus sama. Jika penyebutnya berbeda, maka pecahan harus diubah menjadi pecahan ekuivalen dengan penyebut yang sama.
Setelah penyebut sama, jumlahkan atau kurangkan pembilangnya dan pertahankan penyebutnya.
Contoh:
Menjumlahkan 1/2 dan 1/4:
- Ubah 1/4 menjadi pecahan ekuivalen dengan penyebut 8: 1/4 = 2/8
- Jumlahkan pembilangnya: 1/2 + 2/8 = 4/8 + 2/8 = 6/8
- Pertahankan penyebutnya: 6/8
Mengurangkan 3/5 dari 1:
- Ubah 1 menjadi pecahan: 1 = 5/5
- Kurangkan pembilangnya: 5/5
– 3/5 = 2/5 - Pertahankan penyebutnya: 2/5
Perkalian dan Pembagian Pecahan
Untuk mengalikan pecahan, kalikan pembilang dengan pembilang dan penyebut dengan penyebut.
Untuk membagi pecahan, balik pecahan pembagi dan kalikan dengan pecahan yang dibagi.
Contoh:
Mengalikan 2/3 dengan 1/2:
- Kalikan pembilang dengan pembilang: 2 x 1 = 2
- Kalikan penyebut dengan penyebut: 3 x 2 = 6
- Hasilnya: 2/6
Membagi 1/4 dengan 1/2:
- Balik pecahan pembagi: 1/2 menjadi 2/1
- Kalikan dengan pecahan yang dibagi: 1/4 x 2/1 = 2/4
- Hasilnya: 2/4
Perbandingan Pecahan
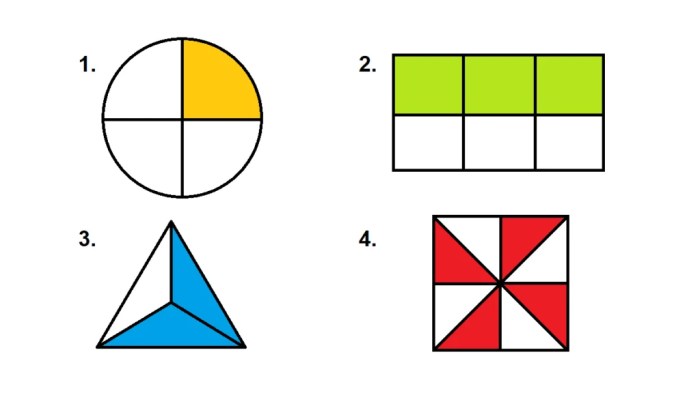
Membandingkan pecahan merupakan keterampilan dasar dalam matematika yang memungkinkan kita menentukan besar kecilnya pecahan dan menentukan hubungan di antara mereka. Ada beberapa metode yang dapat digunakan untuk membandingkan pecahan, baik pecahan senilai maupun pecahan tidak senilai.
Pecahan Senilai
Pecahan senilai adalah pecahan yang memiliki nilai yang sama, meskipun penyebut dan pembilangnya berbeda. Untuk membandingkan pecahan senilai, kita dapat menggunakan metode berikut:
- Menyamakan Penyebut: Ubah kedua pecahan menjadi pecahan senilai dengan penyebut yang sama. Pecahan dengan penyebut terbesar adalah yang lebih besar.
- Membandingkan Pembilang: Jika penyebutnya sama, pecahan dengan pembilang terbesar adalah yang lebih besar.
Pecahan Tidak Senilai
Pecahan tidak senilai adalah pecahan yang memiliki nilai yang berbeda. Untuk membandingkan pecahan tidak senilai, kita dapat menggunakan metode berikut:
- Mengubah ke Desimal: Ubah kedua pecahan menjadi desimal dan bandingkan hasilnya. Pecahan dengan desimal terbesar adalah yang lebih besar.
- Mengubah ke Persen: Ubah kedua pecahan menjadi persen dan bandingkan hasilnya. Pecahan dengan persen terbesar adalah yang lebih besar.
Tabel Perbandingan Pecahan
| Pecahan | Desimal | Persen |
|---|---|---|
| 1/2 | 0,5 | 50% |
| 3/4 | 0,75 | 75% |
| 5/8 | 0,625 | 62,5% |
Dengan menggunakan metode-metode di atas, kita dapat membandingkan pecahan dengan mudah dan menentukan hubungan di antara mereka.
Aplikasi Pecahan dalam Kehidupan Sehari-hari

Pecahan memainkan peran penting dalam berbagai aspek kehidupan kita sehari-hari. Dari memasak hingga mengelola keuangan, pecahan membantu kita mengukur, membagi, dan membandingkan kuantitas.
Dalam Memasak
Saat memasak, kita sering perlu mengukur bahan dalam pecahan. Misalnya, resep mungkin meminta 1/2 cangkir tepung atau 1/4 sendok teh garam. Pemahaman tentang pecahan sangat penting untuk memastikan proporsi bahan yang tepat, sehingga menghasilkan hidangan yang sukses.
Dalam Pembagian Tugas
Pecahan juga digunakan untuk membagi tugas secara adil di antara beberapa orang. Misalnya, jika ada tiga orang yang perlu membersihkan rumah, kita dapat membagi tugas dengan memberikan 1/3 dari tugas kepada masing-masing orang. Ini memastikan bahwa beban kerja didistribusikan secara merata.
Dalam Keuangan
Dalam keuangan, pecahan digunakan untuk mewakili bunga, pajak, dan persentase lainnya. Misalnya, tingkat bunga pinjaman mungkin dinyatakan sebagai 5/100 atau 0,05. Pemahaman tentang pecahan sangat penting untuk menghitung pembayaran pinjaman, pengembalian investasi, dan perhitungan keuangan lainnya.
Contoh Soal Pecahan dan Jawaban
Pemahaman pecahan sangat penting dalam matematika. Pecahan digunakan untuk merepresentasikan bagian dari keseluruhan atau perbandingan antara dua bilangan. Berikut adalah beberapa contoh soal pecahan beserta jawabannya:
Contoh Soal Sederhana
1. Sederhanakan pecahan 6/12.
/12 = (6 ÷ 6) / (12 ÷ 6) = 1/2
Contoh Soal Penjumlahan dan Pengurangan Pecahan
2. Jumlahkan 1/2 dan 1/4.
/2 + 1/4 = (2/4) + (1/4) = 3/4
3. Kurangkan 3/5 dari 1.
- 1
- 3/5 = (5/5)
- (3/5) = 2/5
Contoh Soal Perkalian dan Pembagian Pecahan
4. Kalikan 2/3 dengan 1/2.
/3 × 1/2 = (2 × 1) / (3 × 2) = 1/3
5. Bagi 3/4 dengan 1/2.
/4 ÷ 1/2 = (3/4) × (2/1) = 3/2
Contoh Soal Konversi Pecahan ke Desimal
6. Konversikan pecahan 3/5 ke desimal.
/5 = 0,6
Contoh Soal Konversi Desimal ke Pecahan
7. Konversikan desimal 0,25 ke pecahan.
,25 = 25/100 = 1/4
Akhir Kata

Memahami pecahan sangat penting untuk berbagai aspek kehidupan. Dengan menguasai konsep dan operasi dasar pecahan, Anda akan dapat memecahkan masalah matematika yang kompleks, memahami informasi kuantitatif, dan membuat keputusan yang tepat dalam situasi kehidupan nyata.
Pertanyaan dan Jawaban
Apa saja jenis-jenis pecahan?
Pecahan dapat diklasifikasikan menjadi pecahan biasa, pecahan campuran, dan pecahan desimal.
Bagaimana cara membandingkan pecahan?
Pecahan dapat dibandingkan dengan mencari pecahan senilai atau menggunakan garis bilangan.
Mengapa penting untuk menyederhanakan pecahan?
Menyederhanakan pecahan ke bentuk yang paling sederhana membantu membandingkan dan melakukan operasi pecahan dengan lebih mudah.