Persamaan kuadrat sempurna merupakan konsep mendasar dalam aljabar yang memiliki berbagai aplikasi dalam kehidupan nyata. Artikel ini memberikan gambaran komprehensif tentang persamaan kuadrat sempurna, metode pemfaktorannya, dan contoh soal yang akan mengasah keterampilan Anda.

Persamaan kuadrat sempurna adalah persamaan yang dapat difaktorkan menjadi dua faktor binomial dengan bentuk (x + a)(x + b), di mana a dan b adalah konstanta. Karakteristik unik ini memungkinkan penyelesaian persamaan kuadrat dengan mudah.

Pengertian Persamaan Kuadrat Sempurna

Persamaan kuadrat sempurna adalah persamaan kuadrat yang dapat difaktorkan menjadi bentuk (ax + b)². Persamaan ini memiliki bentuk umum ax² + bx + c = 0, di mana a, b, dan c adalah konstanta real.

Jika persamaan kuadrat memiliki bentuk (ax + b)², maka nilai b² – 4ac = 0. Persamaan ini disebut diskriminan dan menentukan jumlah akar real dari persamaan kuadrat.

Contoh Persamaan Kuadrat Sempurna

• x² + 6x + 9 = 0
• (x
  – 5)² = 0
• 4x²
  – 12x + 9 = 0

Cara Memfaktorkan Persamaan Kuadrat Sempurna

Persamaan kuadrat sempurna adalah persamaan kuadrat yang dapat difaktorkan menjadi dua faktor binomial yang identik. Proses memfaktorkan persamaan kuadrat sempurna melibatkan mengidentifikasi suku yang sesuai dan mengikuti langkah-langkah berikut:

Langkah-langkah Memfaktorkan Persamaan Kuadrat Sempurna

• Tentukan suku konstan (c).
• Cari akar kuadrat dari suku konstan dan bagi dengan 2. Hasilnya adalah setengah dari koefisien suku tengah (b).
• Tuliskan dua suku binomial menggunakan setengah dari koefisien suku tengah sebagai koefisien suku pertama, dan suku konstan sebagai suku terakhir.
• Kuadratkan suku pertama dari setiap suku binomial untuk mendapatkan suku pertama persamaan kuadrat asli.
• Tambahkan kedua suku binomial yang telah dibentuk untuk mendapatkan persamaan kuadrat asli.

Tips Memudahkan Pemfaktoran

• Pastikan persamaan kuadrat berada dalam bentuk standar (ax² + bx + c = 0).
• Cari suku konstan yang merupakan kuadrat sempurna.
• Jika suku konstan bukan kuadrat sempurna, persamaan tersebut tidak dapat difaktorkan menjadi dua faktor binomial yang identik.

Contoh Pemfaktoran Persamaan Kuadrat Sempurna

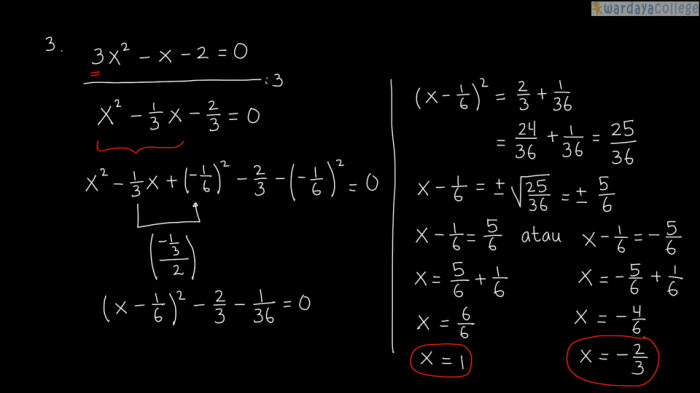
Persamaan kuadrat sempurna adalah persamaan kuadrat yang dapat difaktorkan menjadi dua faktor binomial yang sama. Berikut adalah contoh pemfaktoran persamaan kuadrat sempurna:

Contoh Persamaan Kuadrat Sempurna dan Faktor-Faktornya

Persamaan Kuadrat Sempurna	Faktor-Faktor
x2 4	(x 2)(x + 2)
4x 2 1	(2x 1)(2x + 1)
9y 2 16	(3y 4)(3y + 4)

Langkah-langkah Pemfaktoran Persamaan Kuadrat Sempurna

Untuk memfaktorkan persamaan kuadrat sempurna, ikuti langkah-langkah berikut:

1. Tulis persamaan kuadrat dalam bentuk standar (ax² + bx + c = 0).
2. Keluarkan faktor persekutuan terbesar (FPB) dari semua suku.
3. Tulis suku tengah sebagai penjumlahan atau pengurangan dari dua suku yang hasil kalinya sama dengan hasil kali koefisien suku pertama dan suku terakhir.
4. Gunakan sifat distributif untuk memfaktorkan suku-suku.

Penerapan Persamaan Kuadrat Sempurna dalam Kehidupan Nyata

Persamaan kuadrat sempurna memiliki berbagai aplikasi praktis dalam kehidupan nyata, terutama di bidang fisika, matematika, dan teknik.

Dalam fisika, persamaan kuadrat sempurna digunakan untuk menggambarkan gerakan proyektil, lintasan parabola, dan osilasi harmonik.

Penerapan dalam Fisika

• Gerakan Proyektil: Persamaan kuadrat sempurna digunakan untuk menghitung lintasan proyektil yang dilempar dengan kecepatan dan sudut tertentu.
• Lintasan Parabola: Persamaan kuadrat sempurna dapat digunakan untuk memodelkan lintasan parabola, seperti jalur air mancur atau roket.
• Osilasi Harmonik: Persamaan kuadrat sempurna digunakan untuk menggambarkan osilasi harmonik, seperti gerakan pegas atau bandul.

Dalam matematika, persamaan kuadrat sempurna digunakan untuk menyelesaikan masalah geometri, aljabar, dan kalkulus.

Penerapan dalam Matematika

• Menghitung Luas dan Volume: Persamaan kuadrat sempurna dapat digunakan untuk menghitung luas dan volume bangun ruang, seperti persegi, persegi panjang, dan bola.
• Memfaktorkan Polinomial: Persamaan kuadrat sempurna dapat digunakan untuk memfaktorkan polinomial kuadrat.
• Mencari Ekstremum: Persamaan kuadrat sempurna dapat digunakan untuk mencari titik maksimum atau minimum fungsi kuadrat.

Dalam teknik, persamaan kuadrat sempurna digunakan untuk menganalisis dan merancang sistem listrik, mekanik, dan struktur.

Penerapan dalam Teknik

• Analisis Sirkuit Listrik: Persamaan kuadrat sempurna digunakan untuk menganalisis rangkaian listrik, seperti filter dan penguat.
• Desain Mekanik: Persamaan kuadrat sempurna digunakan untuk merancang struktur mekanis, seperti jembatan dan gedung.
• Analisis Getaran: Persamaan kuadrat sempurna digunakan untuk menganalisis getaran dalam sistem mekanis, seperti mesin dan kendaraan.

Akhir Kata

Memahami persamaan kuadrat sempurna sangat penting untuk menguasai konsep aljabar yang lebih kompleks. Dengan menerapkan langkah-langkah pemfaktoran yang diuraikan dalam artikel ini, Anda akan dapat menyelesaikan berbagai masalah yang melibatkan persamaan kuadrat sempurna. Dari fisika hingga matematika dan teknik, persamaan kuadrat sempurna memiliki peran penting dalam berbagai bidang, menjadikannya topik yang sangat berharga untuk dipelajari.

Pertanyaan Umum yang Sering Muncul

Apa itu persamaan kuadrat sempurna?

Persamaan kuadrat sempurna adalah persamaan kuadrat yang dapat difaktorkan menjadi dua faktor binomial dengan bentuk (x + a)(x + b).

Bagaimana cara memfaktorkan persamaan kuadrat sempurna?

Untuk memfaktorkan persamaan kuadrat sempurna, carilah suku kuadrat yang merupakan kuadrat dari suatu binomial dan suku konstan yang merupakan kuadrat dari suku kedua binomial tersebut.

Apa saja aplikasi persamaan kuadrat sempurna dalam kehidupan nyata?

Persamaan kuadrat sempurna memiliki aplikasi dalam berbagai bidang, seperti fisika (gerak proyektil), matematika (persamaan Diophantine), dan teknik (desain jembatan).