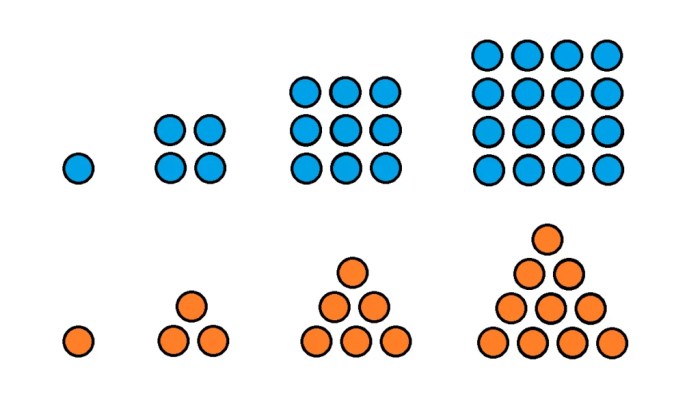Pola bilangan merupakan urutan angka yang mengikuti aturan tertentu. Memahami pola bilangan sangat penting karena membantu kita memprediksi nilai suku berikutnya dalam urutan dan memecahkan masalah yang melibatkan deret angka.
Dalam artikel ini, kita akan membahas konsep dasar pola bilangan, jenis-jenis pola bilangan yang umum, cara menemukan dan menyelesaikan pola bilangan, serta aplikasinya dalam kehidupan nyata.
Pengertian Pola Bilangan
Pola bilangan adalah suatu deret bilangan yang memiliki keteraturan tertentu dalam urutannya. Keteraturan ini dapat berupa penambahan, pengurangan, perkalian, atau pembagian dengan bilangan konstan. Pola bilangan sering ditemukan dalam matematika dan kehidupan sehari-hari.
Contoh Pola Bilangan Sederhana
Salah satu contoh pola bilangan sederhana adalah deret aritmatika. Dalam deret aritmatika, setiap bilangan berikutnya diperoleh dengan menambahkan bilangan konstan yang disebut beda (d) pada bilangan sebelumnya. Misalnya, deret aritmatika dengan suku pertama (a) = 2 dan beda (d) = 3 adalah sebagai berikut:
, 5, 8, 11, 14, …
Jenis-Jenis Pola Bilangan
Pola bilangan adalah urutan bilangan yang mengikuti aturan tertentu. Pola ini banyak ditemukan dalam berbagai bidang, seperti matematika, sains, dan seni. Terdapat beberapa jenis pola bilangan umum, antara lain:
Pola Aritmatika
Pola aritmatika adalah pola bilangan yang selisih antara dua bilangan berurutan selalu sama. Misalnya, pola 2, 4, 6, 8, … memiliki selisih 2.
Pola Geometri
Pola geometri adalah pola bilangan yang hasil bagi antara dua bilangan berurutan selalu sama. Misalnya, pola 2, 4, 8, 16, … memiliki hasil bagi 2.
Pola Fibonacci
Pola Fibonacci adalah pola bilangan di mana setiap bilangan adalah jumlah dari dua bilangan sebelumnya. Pola ini dimulai dengan 0 dan 1, sehingga urutannya menjadi 0, 1, 1, 2, 3, 5, 8, …
Cara Menemukan Pola Bilangan
Mengidentifikasi pola bilangan sangat penting dalam matematika dan pemecahan masalah. Berikut adalah langkah-langkah dan teknik untuk menemukan pola bilangan:
Mencari Selisih Antar Suku
Bandingkan suku-suku yang berurutan untuk menemukan selisih konstan. Misalnya, dalam barisan 2, 5, 8, 11, …, selisih antar suku adalah 3.
Mencari Rasio Antar Suku
Bandingkan suku-suku yang berurutan untuk menemukan rasio konstan. Misalnya, dalam barisan 2, 4, 8, 16, …, rasio antar suku adalah 2.
Cara Menyelesaikan Pola Bilangan
Pola bilangan adalah suatu urutan bilangan yang mengikuti aturan tertentu. Aturan ini dapat berupa penambahan, pengurangan, perkalian, atau pembagian dengan suatu angka konstan.
Untuk menyelesaikan pola bilangan, kita perlu mengidentifikasi aturan yang digunakan dan kemudian menggunakan aturan tersebut untuk menemukan suku berikutnya dalam urutan.
Tabel Cara Menyelesaikan Pola Bilangan Aritmatika
| Jenis Pola | Aturan | Contoh |
|---|---|---|
| Aritmatika | Menambahkan atau mengurangi angka konstan | 2, 4, 6, 8, … |
| Geometris | Mengalikan atau membagi angka konstan | 2, 4, 8, 16, … |
Contoh Soal dan Solusi Langkah demi Langkah
Soal:Tentukan suku ke-10 dari barisan aritmatika 2, 4, 6, 8, …Solusi:1.
-
-*Identifikasi aturan
Pola ini mengikuti aturan penambahan 2.
- 2.
- 3.
- 4.
- 1)
- d, di mana a adalah suku pertama, n adalah nomor suku, dan d adalah beda.
- 5.
- 1)
- 2 = 2 + 9
- 2 = 20
-*Tentukan beda
Beda adalah angka yang ditambahkan pada setiap suku untuk mendapatkan suku berikutnya. Dalam hal ini, bedanya adalah 2.
-*Tentukan suku pertama
Suku pertama diberikan sebagai 2.
-*Tentukan suku ke-n
Rumus untuk suku ke-n barisan aritmatika adalah Un = a + (n
-*Substitusikan nilai
Substitusikan a = 2, n = 10, dan d = 2 ke dalam rumus. Un = 2 + (10
Jadi, suku ke-10 dari barisan aritmatika tersebut adalah 20.
Aplikasi Pola Bilangan
Pola bilangan merupakan urutan bilangan yang mengikuti aturan tertentu. Pola ini memiliki aplikasi yang luas dalam kehidupan nyata, antara lain:
Matematika
- Menyelesaikan deret aritmatika dan geometri
- Memprediksi nilai berikutnya dalam suatu urutan
- Mencari rumus suku ke-n suatu barisan
Sains
- Memprediksi pertumbuhan populasi
- Menganalisis getaran dan gelombang
- Membuat model fenomena alam
Kehidupan Sehari-hari
- Menyusun anggaran keuangan
- Membuat jadwal kerja
- Merencanakan perjalanan
Terakhir

Memahami pola bilangan adalah keterampilan penting yang dapat diterapkan dalam berbagai bidang, mulai dari matematika dan sains hingga kehidupan sehari-hari. Dengan mengenali dan menyelesaikan pola bilangan, kita dapat memperoleh wawasan tentang struktur urutan angka dan membuat prediksi yang tepat.
Sudut Pertanyaan Umum (FAQ)
Apa perbedaan antara pola aritmatika dan geometri?
Pola aritmatika memiliki selisih antar suku yang tetap, sedangkan pola geometri memiliki rasio antar suku yang tetap.
Bagaimana cara menyelesaikan pola bilangan Fibonacci?
Pola Fibonacci mengikuti rumus Fn = Fn-1 + Fn-2, di mana Fn adalah suku ke-n, Fn-1 adalah suku sebelumnya, dan Fn-2 adalah suku dua sebelumnya.
Di mana saja pola bilangan digunakan dalam kehidupan nyata?
Pola bilangan digunakan dalam berbagai aplikasi, seperti memprediksi pertumbuhan populasi, menghitung bunga majemuk, dan merancang struktur bangunan.