Akar rasional, konsep fundamental dalam matematika, memainkan peran penting dalam berbagai aplikasi kehidupan nyata. Artikel ini menyajikan panduan komprehensif tentang akar rasional, dimulai dengan definisi dan contoh, kemudian berlanjut ke teknik penentuan dan penyelesaian soal.

Akar rasional didefinisikan sebagai bilangan rasional yang merupakan akar dari persamaan polinomial dengan koefisien rasional. Konsep ini berbeda dengan akar irasional, yang tidak dapat dinyatakan sebagai pecahan sederhana.

Pengertian Akar Rasional

Akar rasional adalah akar yang dapat dinyatakan sebagai rasio dua bilangan bulat. Dengan kata lain, akar rasional adalah akar yang dapat ditulis dalam bentuk $\surd a/b$ , di mana $a$ dan $b$ adalah bilangan bulat dan $b$ tidak sama dengan nol.

Contoh Akar Rasional dan Non-Rasional

Beberapa contoh akar rasional adalah:

• $\surd 9$ = 3
• $\surd 16/4$ = 2
• $\surd 25/5$ = 5

Sedangkan beberapa contoh akar non-rasional adalah:

• $\surd 2$
• $\surd 3$
• $\surd 5$

Cara Menentukan Akar Rasional

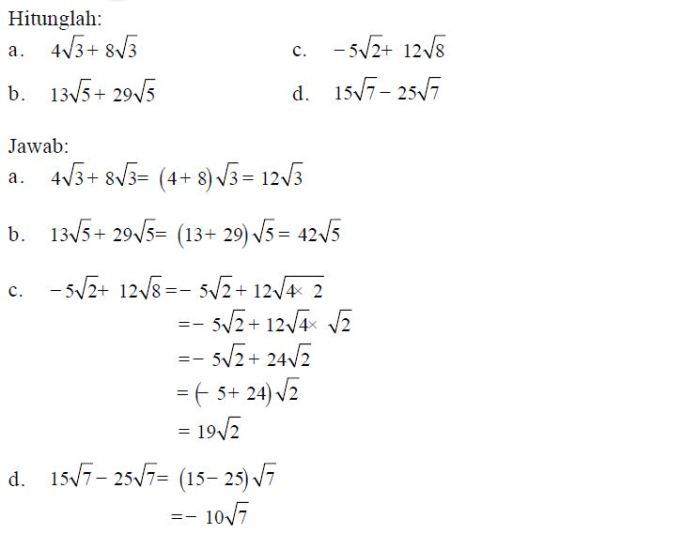
Akar rasional adalah akar dari polinomial dengan koefisien rasional yang dapat dinyatakan dalam bentuk p/q, di mana p dan q adalah bilangan bulat dengan q tidak sama dengan 0. Untuk menentukan akar rasional, dapat digunakan Teorema Rasional Root.

Langkah-langkah Menentukan Akar Rasional

1. Tuliskan polinomial dalam bentuk f(x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x + a₀.
2. Tentukan faktor-faktor dari a₀ dan a_n.
3. Bagilah faktor-faktor a₀ dengan faktor-faktor a_n.
4. Hasil bagi yang diperoleh merupakan calon akar rasional.
5. Substitusikan calon akar rasional ke dalam f(x) untuk memeriksa apakah nilainya sama dengan 0.

Contoh Penentuan Akar Rasional

Tentukan akar rasional dari polinomial f(x) = x ³ – 2x ² – 5x + 6.

1. Faktor-faktor a₀ = 6: 1, 2, 3, 6
2. Faktor-faktor a_n = 1: 1
3. Calon akar rasional: 1, 2, 3, 6
4. Substitusi 1 ke f(x): f(1) = 1³
   • 2(1)²
   • 5(1) + 6 = 0

Jadi, akar rasional dari f(x) adalah 1.

Contoh Soal Akar Rasional

Akar rasional adalah akar dari suatu bilangan yang dapat dinyatakan sebagai pecahan p/q , di mana p dan q adalah bilangan bulat dan q tidak sama dengan nol.

Contoh Soal

Berikut adalah beberapa contoh soal akar rasional yang beragam:

Soal	Penyelesaian	Jawaban	Tingkat Kesulitan
Sederhanakan $\sqrt{12}$	$\sqrt{12}=\; \backslash msqrt>4\cdot 3=\; 2\backslash msqrt>3$	$2\backslash msqrt>3$	Mudah
Rasionalkan penyebut dari $\frac{1}{\sqrt{5}}$	$\frac{1}{\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}}=\; \backslash frac\backslash sqrt>55$	$\backslash frac\backslash sqrt>55$	Sedang
Sederhanakan $\sqrt{\frac{16}{25}}$	$\sqrt{\frac{16}{25}}=\; \backslash frac\backslash msqrt>16\sqrt{25}=\; \backslash frac45$	$\backslash frac45$	Sulit

Prosedur Penyelesaian Soal Akar Rasional

Menyelesaikan soal akar rasional melibatkan penyederhanaan ekspresi yang mengandung akar ke dalam bentuk yang lebih sederhana dan rasional. Berikut adalah prosedur umum untuk menyelesaikan soal akar rasional:

Penyederhanaan Ekspresi

• Identifikasi semua akar dalam ekspresi.
• Rasionalisasi penyebut dengan mengalikan dan membagi dengan bentuk konjugat penyebut.
• Sederhanakan ekspresi dengan mengalikan suku-suku yang serupa dan melakukan operasi aritmatika.

Contoh Soal

Sederhanakan ekspresi berikut:

$$\frac1\sqrt2 + 1$$

Langkah-langkah Penyelesaian

1. Bentuk konjugat dari penyebut adalah $\sqrt2
   

   1$.

2. Rasionalisasi penyebut dengan mengalikan dan membagi dengan bentuk konjugat:

$$\frac1\sqrt2 + 1 \cdot \frac\sqrt2

• 1\sqrt2
• 1$$
3. Sederhanakan ekspresi:

$$\frac\sqrt2

• 12
• 1$$
4. Hasil akhir:

$$\sqrt2

1$$

Aplikasi Akar Rasional

Akar rasional memiliki banyak aplikasi dalam kehidupan sehari-hari, matematika, dan bidang lainnya.

Matematika

• Menyederhanakan persamaan dan ekspresi
• Menghitung luas dan volume bentuk geometris
• Memecahkan persamaan kuadrat

Fisika

• Menghitung kecepatan benda yang bergerak dengan percepatan konstan
• Menghitung panjang gelombang cahaya
• Menghitung energi potensial suatu benda

Bidang Lainnya

• Ekonomi: Menghitung tingkat pertumbuhan ekonomi
• Biologi: Menghitung laju pertumbuhan populasi

li>Teknik: Menghitung kekuatan dan tegangan material

Rangkuman dan Tips

Rakarasional adalah bilangan yang dapat diekspresikan sebagai pecahan dengan penyebut yang rasional. Untuk menguasai penyelesaian soal akar rasional, penting untuk memahami konsep dasarnya dan menerapkan teknik yang tepat.

Rangkuman Poin-Poin Penting

• Rakarasional adalah bilangan yang dapat diekspresikan sebagai pecahan dengan penyebut rasional.
• Akar rasional dapat disederhanakan dengan memfaktorkan penyebut dan merasionalisasi pembilangnya.
• Untuk menyelesaikan soal akar rasional, penting untuk memahami sifat-sifat akar dan cara memanipulasinya.

Tips untuk Menguasai Soal Akar Rasional

• Pahami sifat-sifat akar, seperti √(ab) = √a√b dan (√a + √b)² = a + 2√ab + b.
• Latih soal secara teratur untuk meningkatkan keterampilan dan kepercayaan diri.
• Gunakan kalkulator hanya untuk memeriksa jawaban, bukan sebagai alat bantu utama.
• Berkonsultasilah dengan guru atau tutor jika mengalami kesulitan.

Ringkasan Penutup

Menguasai konsep akar rasional sangat penting untuk keberhasilan dalam matematika dan aplikasi terkait. Dengan memahami dasar-dasarnya dan mempraktikkan teknik penyelesaian, individu dapat mengatasi berbagai soal akar rasional dengan percaya diri.

Tanya Jawab (Q&A)

Apa perbedaan antara akar rasional dan akar irasional?

Akar rasional adalah bilangan rasional yang merupakan akar dari persamaan polinomial dengan koefisien rasional, sedangkan akar irasional tidak dapat dinyatakan sebagai pecahan sederhana.

Bagaimana cara menentukan akar rasional?

Akar rasional dapat ditentukan dengan menggunakan teorema rasional, yang menyatakan bahwa setiap akar rasional dari persamaan polinomial dengan koefisien bilangan bulat adalah pembagi dari konstanta persamaan tersebut.

Apa saja aplikasi akar rasional?

Akar rasional memiliki aplikasi luas dalam matematika, fisika, dan bidang lainnya, termasuk pemecahan persamaan, perhitungan panjang dan volume, serta analisis fungsi.