Contoh soal simpangan rata rata data tunggal – Dalam statistik, simpangan rata-rata data tunggal menjadi salah satu ukuran penyebaran data yang penting. Konsep ini mengukur seberapa jauh nilai data menyimpang dari nilai rata-rata, memberikan wawasan tentang variabilitas data.

Artikel ini akan membahas secara mendalam tentang contoh soal simpangan rata-rata data tunggal, meliputi pengertian, rumus perhitungan, jenis-jenis, dan prosedur pengerjaan. Dengan memahami konsep ini, Anda dapat menganalisis data statistik secara lebih komprehensif dan membuat keputusan yang lebih tepat.

Pengertian Simpangan Rata-rata Data Tunggal

Simpangan rata-rata data tunggal adalah ukuran seberapa jauh setiap data dalam suatu kumpulan data menyimpang dari nilai rata-rata. Nilai ini digunakan untuk mengukur variabilitas atau penyebaran data.

Dalam statistik, contoh soal simpangan rata-rata data tunggal membantu kita memahami konsep variabilitas. Salah satu aspek penting dalam pembuatan dokumen andal rkl dan rpl dibuat adalah memastikan akurasi data . Untuk itu, contoh soal simpangan rata-rata data tunggal dapat diterapkan dalam menguji reliabilitas data, sehingga dokumen yang dihasilkan dapat diandalkan untuk pengambilan keputusan yang tepat.

Rumus Perhitungan Simpangan Rata-rata Data Tunggal

Rumus untuk menghitung simpangan rata-rata data tunggal adalah sebagai berikut:“`Simpangan rata-rata = (Nilai data

Nilai rata-rata) / Jumlah data

“`Dalam rumus tersebut, nilai data adalah nilai setiap data dalam kumpulan data, nilai rata-rata adalah rata-rata dari semua nilai data, dan jumlah data adalah jumlah total data dalam kumpulan data.

Cara Menghitung Simpangan Rata-rata Data Tunggal

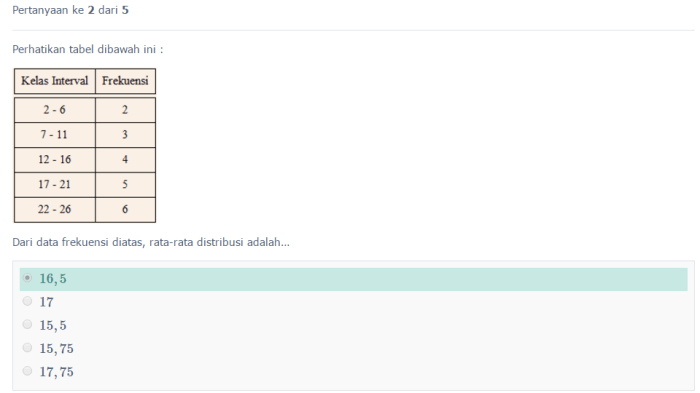
Simpangan rata-rata data tunggal mengukur seberapa jauh nilai data dari rata-ratanya. Berikut langkah-langkah menghitungnya:

Mencari Rata-rata

Hitung rata-rata data dengan menjumlahkan semua nilai dan membaginya dengan jumlah data. Misal, data: 5, 7, 9, 11, 13. Rata-rata = (5 + 7 + 9 + 11 + 13) / 5 = 9.

Menghitung Simpangan dari Rata-rata

Untuk setiap nilai data, kurangi rata-rata untuk mendapatkan simpangan dari rata-rata. Misal, simpangan data 5 dari rata-rata 9 adalah 5 – 9 = -4.

Mengkuadratkan Simpangan

Kuadratkan setiap simpangan dari rata-rata untuk menghilangkan nilai negatif. Misal, simpangan -4 dikuadratkan menjadi 16.

Menjumlahkan Kuadrat Simpangan

Jumlahkan semua kuadrat simpangan. Misal, kuadrat simpangan data 5, 7, 9, 11, 13 adalah 16 + 4 + 0 + 4 + 16 = 40.

Mencari Varian

Bagilah jumlah kuadrat simpangan dengan jumlah data dikurangi 1 (n-1). Ini disebut variansi. Misal, variansi = 40 / (5-1) = 10.

Mencari Simpangan Rata-rata

Ambil akar kuadrat dari variansi untuk mendapatkan simpangan rata-rata. Misal, simpangan rata-rata = √10 ≈ 3,16.

Contoh Soal

Hitung simpangan rata-rata dari data berikut: 4, 6, 8, 10, 12.

Rata-rata = (4 + 6 + 8 + 10 + 12) / 5 = 8.

Simpangan: 4-8 = -4, 6-8 = -2, 8-8 = 0, 10-8 = 2, 12-8 = 4.

Kuadrat Simpangan: 16, 4, 0, 4, 16.

Jumlah Kuadrat Simpangan: 40.

Varian: 40 / (5-1) = 10.

Simpangan Rata-rata: √10 ≈ 3,16.

Jenis-jenis Simpangan Rata-rata Data Tunggal

Simpangan rata-rata data tunggal adalah ukuran yang digunakan untuk mengukur seberapa tersebar data dari rata-rata atau nilai tengahnya. Terdapat beberapa jenis simpangan rata-rata data tunggal, masing-masing dengan tujuan dan penggunaannya yang berbeda.

Simpangan Rata-rata Mutlak (Mean Absolute Deviation), Contoh soal simpangan rata rata data tunggal

Simpangan rata-rata mutlak adalah rata-rata dari perbedaan absolut antara setiap nilai data dengan rata-rata. Ini mengukur penyebaran data tanpa mempertimbangkan tanda perbedaan. Simpangan rata-rata mutlak lebih robust terhadap nilai ekstrem dibandingkan simpangan baku.

Simpangan Rata-rata Kuadrat (Root Mean Square Deviation)

Simpangan rata-rata kuadrat adalah akar kuadrat dari rata-rata kuadrat perbedaan antara setiap nilai data dengan rata-rata. Ini memberikan bobot yang lebih besar pada nilai ekstrem dibandingkan simpangan rata-rata mutlak. Simpangan rata-rata kuadrat sering digunakan dalam aplikasi statistik, seperti analisis regresi.

Contoh soal simpangan rata-rata data tunggal melibatkan perhitungan jarak antara setiap titik data dan nilai rata-rata. Teknik ini juga diterapkan dalam menentukan kutub magnet dengan cara induksi , di mana arah induksi medan magnet digunakan untuk mengidentifikasi kutub utara dan selatan magnet.

Dengan memahami simpangan rata-rata, peneliti dapat menentukan akurasi pengukuran mereka dan mengevaluasi keandalan hasil yang diperoleh.

Simpangan Baku (Standard Deviation)

Simpangan baku adalah akar kuadrat dari varians, yang merupakan rata-rata kuadrat perbedaan antara setiap nilai data dengan rata-rata. Simpangan baku adalah ukuran penyebaran data yang umum digunakan dan memberikan informasi tentang seberapa tersebar data dari rata-rata. Simpangan baku sensitif terhadap nilai ekstrem.

Simpangan Kuartil (Quartile Deviation)

Simpangan kuartil adalah setengah dari perbedaan antara kuartil ketiga dan kuartil pertama. Ini memberikan ukuran penyebaran data yang tidak terpengaruh oleh nilai ekstrem. Simpangan kuartil sering digunakan dalam analisis data eksplorasi.

Pemilihan Jenis Simpangan Rata-rata

Pemilihan jenis simpangan rata-rata yang tepat tergantung pada tujuan analisis dan sifat data. Simpangan rata-rata mutlak cocok untuk data dengan nilai ekstrem, sedangkan simpangan rata-rata kuadrat lebih cocok untuk data yang mengikuti distribusi normal. Simpangan baku adalah ukuran penyebaran yang umum digunakan, tetapi sensitif terhadap nilai ekstrem.

Dalam contoh soal simpangan rata-rata data tunggal, menghitung jarak data dari rata-rata memberikan pemahaman tentang penyebaran data. Analogi serupa dapat diterapkan pada pertanyaan apakah pembaruan perangkat lunak memakan RAM ( apakah pembaruan perangkat lunak memakan ram ). Pembaruan perangkat lunak dapat menambah beban pada memori sistem, sehingga meningkatkan simpangan dari penggunaan RAM rata-rata.

Oleh karena itu, pemahaman tentang simpangan rata-rata dalam contoh soal dapat membantu mengidentifikasi dampak potensial pembaruan perangkat lunak pada konsumsi RAM.

Simpangan kuartil tidak terpengaruh oleh nilai ekstrem dan berguna untuk analisis data eksplorasi.

Contoh Soal Simpangan Rata-rata Data Tunggal: Contoh Soal Simpangan Rata Rata Data Tunggal

Simpangan rata-rata adalah ukuran penyebaran data yang menunjukkan seberapa jauh data individu menyimpang dari nilai rata-ratanya. Berikut adalah beberapa contoh soal simpangan rata-rata data tunggal:

Data Nilai Ujian

Sebuah kelas terdiri dari 10 siswa dengan nilai ujian sebagai berikut:

• 75
• 80
• 85
• 90
• 95
• 80
• 75
• 90
• 85
• 80

Nilai rata-rata (mean) kelas tersebut adalah 82, 5. Simpangan rata-rata dapat dihitung menggunakan rumus:

Simpangan Rata-rata = √(∑(xi

• x̄)² / (n
• 1))

Dengan xi adalah nilai data, x̄ adalah mean, dan n adalah jumlah data.

Dengan menggunakan rumus tersebut, simpangan rata-rata untuk data nilai ujian tersebut adalah 6,93.

Data Tinggi Badan

Sebuah survei terhadap 20 orang menghasilkan data tinggi badan sebagai berikut (dalam cm):

• 165
• 170
• 175
• 180
• 185
• 170
• 165
• 180
• 175
• 180
• 165
• 170
• 175
• 180
• 185
• 170
• 165
• 180
• 175
• 180

Nilai rata-rata tinggi badan adalah 175 cm. Simpangan rata-rata dapat dihitung menjadi 5,29 cm.

Prosedur Pengerjaan Contoh Soal

Pengerjaan contoh soal simpangan rata-rata data tunggal melibatkan beberapa langkah sistematis untuk menentukan nilai simpangan rata-rata.

Langkah-Langkah Pengerjaan

1. Menentukan Mean (Rata-rata)

   Menghitung rata-rata dari kumpulan data untuk mendapatkan nilai referensi.

2. Menghitung Selisih Tiap Data dari Mean

   Mengurangkan tiap data dari nilai mean yang telah ditentukan.

3. Mengkuadratkan Selisih

   Mengkuadratkan hasil selisih tiap data dari mean.

4. Menjumlahkan Kuadrat Selisih

   Menjumlahkan semua nilai kuadrat selisih yang telah dihitung.

5. Menghitung Varians

   Membagi jumlah kuadrat selisih dengan jumlah data untuk mendapatkan varians.

6. Menghitung Simpangan Rata-rata

   Mengambil akar kuadrat dari varians untuk memperoleh nilai simpangan rata-rata.

Tips Menyelesaikan Contoh Soal Simpangan Rata-rata Data Tunggal

Menyelesaikan contoh soal simpangan rata-rata data tunggal dapat menjadi tugas yang menantang. Namun, dengan strategi dan pendekatan yang tepat, Anda dapat memecahkan masalah ini dengan mudah.

Langkah-langkah Umum

1. Pahami konsep simpangan rata-rata dan rumusnya.
2. Identifikasi data yang diberikan dalam soal.
3. Gunakan rumus simpangan rata-rata untuk menghitung simpangan setiap data dari rata-rata.
4. Jumlahkan kuadrat simpangan.
5. Bagikan jumlah kuadrat simpangan dengan jumlah data.
6. Ambil akar kuadrat dari hasil pada langkah sebelumnya untuk mendapatkan simpangan rata-rata.

Tips Tambahan

• Perhatikan unit pengukuran data yang diberikan.
• Jika data memiliki banyak nilai, gunakan kalkulator atau spreadsheet untuk menghitung simpangan rata-rata.
• Latih soal sebanyak mungkin untuk meningkatkan keterampilan Anda.
• Jika memungkinkan, gunakan contoh soal yang mirip dengan soal ujian yang akan Anda hadapi.

Aplikasi Simpangan Rata-rata Data Tunggal

Simpangan rata-rata data tunggal merupakan ukuran statistik yang digunakan untuk mengukur seberapa jauh data menyebar dari nilai rata-rata. Ini memiliki berbagai aplikasi di berbagai bidang, antara lain:

Bidang Statistika dan Probabilitas

• Menguji hipotesis dan membuat prediksi
• Mengevaluasi model distribusi data
• Membandingkan dua atau lebih kumpulan data

Bidang Keuangan dan Bisnis

• Menganalisis risiko dan pengembalian investasi
• Memprediksi fluktuasi harga saham
• Mengevaluasi kinerja keuangan perusahaan

Bidang Ilmu Pengetahuan Alam

• Menganalisis variasi data pengukuran eksperimental
• Memprediksi hasil eksperimen berdasarkan data sebelumnya
• Membandingkan metode eksperimental yang berbeda

Bidang Ilmu Sosial

• Menganalisis variasi dalam data survei
• Memprediksi perilaku individu dan kelompok
• Mengevaluasi efektivitas program sosial

Bidang Teknik dan Manufaktur

• Menganalisis variasi dalam proses manufaktur
• Memprediksi kegagalan komponen
• Mengevaluasi kinerja sistem teknik

Akhir Kata

Contoh soal simpangan rata-rata data tunggal memberikan pemahaman yang jelas tentang konsep ini dan aplikasinya dalam berbagai bidang. Dengan memahami rumus, jenis, dan prosedur pengerjaannya, Anda dapat menganalisis data secara efektif dan memperoleh kesimpulan yang valid. Simpangan rata-rata data tunggal menjadi alat yang berharga dalam penelitian statistik, memungkinkan kita untuk mengukur penyebaran data dan membuat keputusan yang lebih tepat berdasarkan informasi yang diperoleh.

Panduan FAQ

Apa itu simpangan rata-rata data tunggal?

Simpangan rata-rata data tunggal adalah ukuran penyebaran data yang menunjukkan seberapa jauh nilai data menyimpang dari nilai rata-rata.

Bagaimana rumus perhitungan simpangan rata-rata data tunggal?

Rumus perhitungan simpangan rata-rata data tunggal adalah akar kuadrat dari varian, yaitu akar kuadrat dari jumlah kuadrat selisih nilai data dan nilai rata-rata dibagi dengan jumlah data dikurangi 1.

Apa saja jenis-jenis simpangan rata-rata data tunggal?

Jenis-jenis simpangan rata-rata data tunggal antara lain simpangan rata-rata sampel dan simpangan rata-rata populasi.