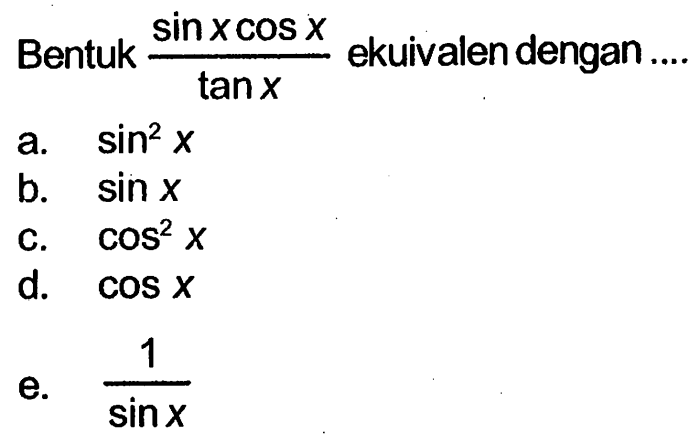Dalam dunia trigonometri, cosinus 610 derajat merupakan konsep yang menarik dan penting. Sudut yang tidak biasa ini memiliki nilai cosinus yang unik dan berhubungan dengan sudut lain yang memiliki nilai cosinus yang sama. Penjelajahan ekuivalen trigonometri cosinus 610 derajat akan mengungkap sifat-sifat sudut ini dan aplikasinya dalam berbagai bidang.
Konsep cosinus dan perhitungannya untuk sudut 610 derajat akan dibahas secara mendalam. Selanjutnya, kita akan mengidentifikasi sudut-sudut lain yang memiliki nilai cosinus yang sama dan menyusun tabel ekuivalen trigonometri untuk cosinus 610 derajat. Aplikasi cosinus 610 derajat dalam geometri akan diilustrasikan dengan contoh nyata, dan signifikansi matematisnya akan dieksplorasi melalui hubungannya dengan bilangan kompleks dan identitas trigonometri.
Cosinus 610 Derajat
Cosinus adalah fungsi trigonometri yang mengukur perbandingan sisi berdekatan dengan sisi miring dalam segitiga siku-siku. Untuk sudut 610 derajat, kita dapat menggunakan rumus berikut:
cos 610° = cos (610° – 360°) = cos 250°
Langkah-langkah Perhitungan
- Kurangi 360 derajat dari 610 derajat untuk mendapatkan sudut antara 0 dan 360 derajat, yaitu 250 derajat.
- Gunakan tabel trigonometri atau kalkulator untuk mencari nilai cosinus 250 derajat, yang kira-kira
0,9063.
Ekuivalen Trigonometri

Cosinus 610 derajat dapat diekspresikan sebagai ekuivalen trigonometrinya menggunakan sifat periodisitas dan simetri fungsi cosinus.
Karena fungsi cosinus memiliki periode 360 derajat, sudut 610 derajat dapat direduksi menjadi sudut ekuivalen dalam interval [0, 360) derajat.
Sudut Ekuivalen
- Kurangi 360 derajat dari 610 derajat: 610°
– 360° = 250° - Karena cosinus adalah fungsi genap, cosinus 250 derajat sama dengan cosinus (-250 derajat): cos 250° = cos (-250°)
Tabel Ekuivalen Trigonometri
| Sudut | Ekuivalen Cosinus |
|---|---|
| 610° | cos 250° |
| -250° | cos 250° |
Aplikasi dalam Geometri

Cosinus 610 derajat, meskipun bukan sudut standar dalam geometri, dapat digunakan untuk menghitung panjang sisi dan sudut segitiga dalam kasus-kasus tertentu.
Menggunakan Cosinus 610 Derajat untuk Menentukan Panjang Sisi
Dalam segitiga sembarang, panjang sisi c yang berhadapan dengan sudut C dapat dihitung menggunakan rumus:
c 2 = a 2 + b 2
2 ab cos C
di mana a dan b adalah panjang dua sisi lainnya dan C adalah sudut di hadapan sisi c .
Menggunakan Cosinus 610 Derajat untuk Menentukan Sudut
Cosinus 610 derajat juga dapat digunakan untuk menentukan sudut segitiga. Dalam segitiga sembarang, sudut C yang berhadapan dengan sisi c dapat dihitung menggunakan rumus:
cos C = ( a 2 + b 2
c 2 ) / 2 ab
di mana a , b , dan c adalah panjang sisi segitiga.
Contoh Penggunaan Cosinus 610 Derajat dalam Geometri
Misalkan kita memiliki segitiga dengan sisi a = 5 cm, b = 7 cm, dan sudut C = 610 derajat. Kita dapat menggunakan rumus di atas untuk menghitung panjang sisi c :
c 2 = 5 2 + 7 2
2(5)(7)cos610°
c 2 = 25 + 49
70(-0,951)
c 2 = 25 + 49 + 66,57 c 2 = 140,57 c ≈ 11,85 cm
Oleh karena itu, panjang sisi c kira-kira 11,85 cm.
Signifikansi dalam Matematika
Cosinus 610 derajat memiliki signifikansi penting dalam matematika, terutama dalam konteks bilangan kompleks dan identitas trigonometri.
Hubungan dengan Bilangan Kompleks
Dalam bidang bilangan kompleks, cosinus 610 derajat dapat diekspresikan sebagai:
Ini karena 610 derajat setara dengan 2π radian, yang merupakan satu putaran penuh pada lingkaran satuan. Cosinus dari 2π radian selalu -1, karena mewakili titik pada sumbu horizontal negatif.
Identitas Trigonometri
Cosinus 610 derajat juga terkait dengan identitas trigonometri lainnya, seperti:
- cos(610°) = cos(180° + 430°)
- cos(610°) =
-cos(250°) - cos(610°) = 1/2(cos(305°) + cos(815°))
Identitas ini dapat digunakan untuk menyelesaikan persamaan trigonometri dan membuktikan teorema lainnya.
Penerapan dalam Teorema
Cosinus 610 derajat juga muncul dalam teorema tertentu, seperti:
- Teorema Cosinus Umum: c² = a² + b²
– 2ab cos(C) - Teorema Sinus: a/sin(A) = b/sin(B) = c/sin(C)
Dalam teorema ini, cosinus 610 derajat dapat digunakan untuk menghitung panjang sisi atau sudut segitiga.
Terakhir

Ekuivalen trigonometri cosinus 610 derajat memberikan wawasan tentang sifat sudut yang tidak biasa ini. Sudut-sudut yang memiliki nilai cosinus yang sama saling terkait, menciptakan hubungan simetri dalam sistem koordinat trigonometri. Signifikansi matematis cosinus 610 derajat melampaui trigonometri, terhubung dengan konsep matematika yang lebih luas dan menyediakan alat yang ampuh untuk memecahkan masalah geometri dan memahami sifat bilangan kompleks.
Pertanyaan Umum (FAQ)
Apa hubungan antara cosinus 610 derajat dan cosinus 250 derajat?
Cosinus 610 derajat sama dengan cosinus 250 derajat karena kedua sudut tersebut merupakan sudut coterminal.
Apakah cosinus 610 derajat positif atau negatif?
Cosinus 610 derajat adalah positif karena berada pada kuadran pertama.
Dalam aplikasi apa cosinus 610 derajat digunakan?
Cosinus 610 derajat dapat digunakan dalam aplikasi geometri, seperti menghitung panjang sisi atau sudut segitiga.