Dalam matematika, deret aritmatika merupakan urutan bilangan yang memiliki selisih konstan antar suku-sukunya. Pemahaman mengenai deret aritmatika sangat penting dalam berbagai aplikasi kehidupan nyata, mulai dari perhitungan keuangan hingga analisis data.

Pada kesempatan ini, kita akan membahas deret aritmatika lebih mendalam, menggunakan contoh deret 4, 19, 34 sebagai acuan. Melalui analisis deret ini, kita akan mengungkap sifat-sifat, rumus, dan penerapan deret aritmatika dalam berbagai bidang.

Pengertian Deret Aritmatika

Deret aritmatika adalah suatu barisan bilangan yang memiliki beda tetap antar suku-sukunya.

Dengan kata lain, setiap suku dalam deret aritmatika diperoleh dengan menambahkan atau mengurangkan suatu bilangan tetap (beda) dari suku sebelumnya.

Contoh Deret Aritmatika

• 4, 7, 10, 13, 16, … (beda = 3)
• 10, 15, 20, 25, 30, … (beda = 5)
• 5, 2,
  -1,
  -4,
  -7, … (beda =
  -3)

Rumus Deret Aritmatika

Deret aritmatika adalah suatu barisan bilangan yang memiliki beda yang sama antar setiap suku.

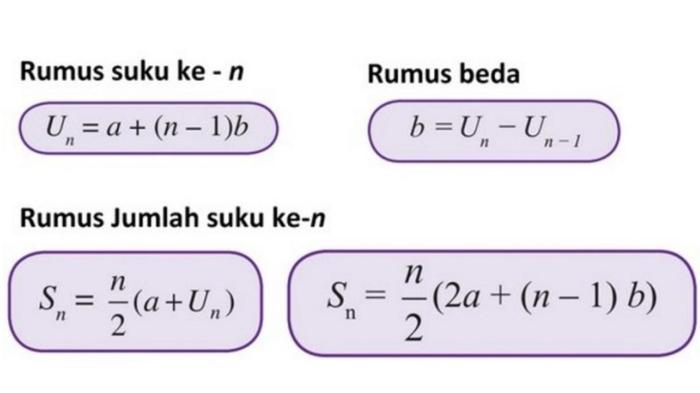
Rumus suku ke-n deret aritmatika adalah:

$$U_n = a + (n

1)b$$

di mana:

• $U_n$ adalah suku ke-n
• $a$ adalah suku pertama
• $b$ adalah beda
• $n$ adalah nomor suku

Mengidentifikasi Deret Aritmatika

Deret aritmatika adalah suatu barisan bilangan yang memiliki beda tetap antara setiap suku berurutan. Untuk mengidentifikasi deret aritmatika, terdapat beberapa cara yang dapat digunakan:

Ciri-ciri Khas Deret Aritmatika

• Perbedaan antara dua suku berurutan adalah konstan.
• Rasio antara dua suku berurutan adalah sama.
• Deret dapat direpresentasikan dalam bentuk persamaan suku ke-n, yaitu Un = a + (n-1)b, di mana a adalah suku pertama, b adalah beda, dan n adalah nomor urut suku.

Mencari Beda dan Suku Pertama

Dalam deret aritmatika, suku pertama dan beda merupakan dua parameter penting yang menentukan sifat deret. Berikut langkah-langkah untuk mencari beda dan suku pertama deret aritmatika:

Tabel Penjelasan Proses Pencarian

Langkah	Penjelasan
1. Mencari Beda	Kurangi suku kedua dengan suku pertama: b = u2 u 1
2. Mencari Suku Pertama	Gunakan suku pertama dan beda untuk menghitung suku pertama: u1 = un (n-1)b

Menentukan Suku ke-n

Dalam deret aritmatika, suku ke-n dapat ditentukan menggunakan rumus berikut:

Rumus Suku ke-n

Un = a + (n – 1) – b

Keterangan:

• Un: Suku ke-n
• a: Suku pertama
• n: Nomor urut suku
• b: Beda

Contoh Penggunaan

Misalkan kita memiliki deret aritmatika 4, 19, 34. Suku pertama (a) adalah 4, dan bedanya (b) adalah 15. Untuk menentukan suku ke-10 (n = 10), kita gunakan rumus:

U10 = 4 + (10 – 1) – 15 = 4 + 9 – 15 = 139

Sifat-Sifat Deret Aritmatika

Deret aritmatika memiliki sifat-sifat tertentu yang membedakannya dari jenis deret lainnya. Sifat-sifat ini mencakup jumlah suku, jumlah suku genap, dan jumlah suku ganjil.

Jumlah Suku

• Jumlah n suku pertama deret aritmatika dengan suku pertama a dan beda b diberikan oleh rumus:

• S n = n /2( a + a n )

Jumlah Suku Genap

• Jumlah n suku genap pertama deret aritmatika dengan suku pertama a dan beda b diberikan oleh rumus:

• S g = n /4( a + a n + 2 b n /2)

Jumlah Suku Ganjil

• Jumlah n suku ganjil pertama deret aritmatika dengan suku pertama a dan beda b diberikan oleh rumus:

• S g = n /4( a + a n – 2 b n /2)

Aplikasi Deret Aritmatika

Deret aritmatika memiliki banyak aplikasi dalam kehidupan nyata. Mereka digunakan dalam berbagai bidang, termasuk keuangan, fisika, dan teknik.

Aplikasi dalam Keuangan

• Menghitung bunga majemuk: Deret aritmatika digunakan untuk menghitung bunga yang diperoleh dari investasi dari waktu ke waktu.
• Merencanakan pembayaran pinjaman: Deret aritmatika dapat digunakan untuk membuat jadwal pembayaran pinjaman, yang menunjukkan jumlah pembayaran dan saldo pinjaman yang tersisa setiap bulan.

Aplikasi dalam Fisika

• Gerak benda beraturan: Deret aritmatika dapat digunakan untuk menghitung jarak yang ditempuh oleh benda yang bergerak dengan kecepatan konstan.
• Getaran harmonik: Deret aritmatika digunakan untuk memodelkan gerakan benda yang bergetar, seperti pegas atau bandul.

Aplikasi dalam Teknik

• Merancang struktur: Deret aritmatika digunakan untuk menghitung beban yang dapat ditahan oleh struktur, seperti jembatan atau bangunan.
• Menganalisis data: Deret aritmatika dapat digunakan untuk menganalisis data dan mengidentifikasi tren atau pola.

Penutup

Kesimpulannya, deret aritmatika merupakan konsep penting dalam matematika yang memiliki banyak aplikasi praktis. Dengan memahami sifat-sifat dan rumus yang terkait, kita dapat memecahkan berbagai masalah dan membuat prediksi yang akurat dalam berbagai bidang kehidupan.

Pertanyaan Umum yang Sering Muncul

Apa yang dimaksud dengan beda dalam deret aritmatika?

Beda adalah selisih konstan antar suku-suku dalam deret aritmatika.

Bagaimana cara mencari suku ke-n dalam deret aritmatika?

Suku ke-n (Un) dalam deret aritmatika dapat dicari menggunakan rumus Un = a + (n – 1) – b, di mana a adalah suku pertama dan b adalah beda.

Apa saja sifat-sifat deret aritmatika?

Deret aritmatika memiliki sifat-sifat seperti jumlah suku genap, jumlah suku ganjil, dan jumlah n suku pertama.