Segitiga, sosok geometri yang umum ditemukan di sekitar kita, memiliki peran penting dalam berbagai bidang. Segitiga ABC, khususnya, menjadi dasar bagi pemahaman konsep segitiga yang lebih kompleks. Dengan sifat, rumus, dan aplikasinya yang unik, segitiga ABC menjadi topik yang menarik untuk dipelajari.

Dalam uraian ini, kita akan menyelidiki sifat-sifat penting segitiga ABC, mengeksplorasi rumus yang terkait, dan mengungkap aplikasi praktisnya. Pengetahuan ini akan memberikan pemahaman yang lebih mendalam tentang geometri dan aplikasinya di dunia nyata.

Deskripsi Segitiga ABC

Segitiga ABC adalah segitiga sembarang dengan tiga sisi dan tiga sudut.

Sifat-sifat segitiga ABC adalah sebagai berikut:

• Sisi-sisinya:
• AB, BC, dan AC
• Sudut-sudutnya:
• ∠A, ∠B, dan ∠C
• Jenis segitiga:
• Tergantung pada panjang sisinya dan besar sudutnya, segitiga ABC dapat diklasifikasikan sebagai segitiga siku-siku, segitiga sama sisi, atau segitiga sembarang.

Ilustrasi Segitiga ABC

Berikut adalah ilustrasi segitiga ABC yang berlabel:

[Ilustrasi segitiga ABC dengan label untuk sisi dan sudutnya]

Rumus Terkait Segitiga ABC

Segitiga ABC memiliki tiga sisi dan tiga sudut. Rumus berikut dapat digunakan untuk menghitung keliling dan luas segitiga ABC.

Keliling Segitiga ABC

• K = a + b + c
• di mana K adalah keliling, dan a, b, dan c adalah panjang ketiga sisi segitiga.

Luas Segitiga ABC

• L = (1/2)
  – a
  – h
• di mana L adalah luas, a adalah panjang alas, dan h adalah tinggi segitiga.

Tabel Rumus

Rumus	Keterangan
K = a + b + c	Keliling
L = (1/2) a h	Luas

Teorema dan Sifat Segitiga ABC

Teorema Pythagoras

tentang Teorema Pythagoras

• Detail 1
• Detail 2

Sifat Sudut Dalam dan Luar Segitiga ABC

tentang sifat sudut dalam dan luar segitiga ABC

• Sifat 1
• Sifat 2

Perhitungan Segitiga ABC

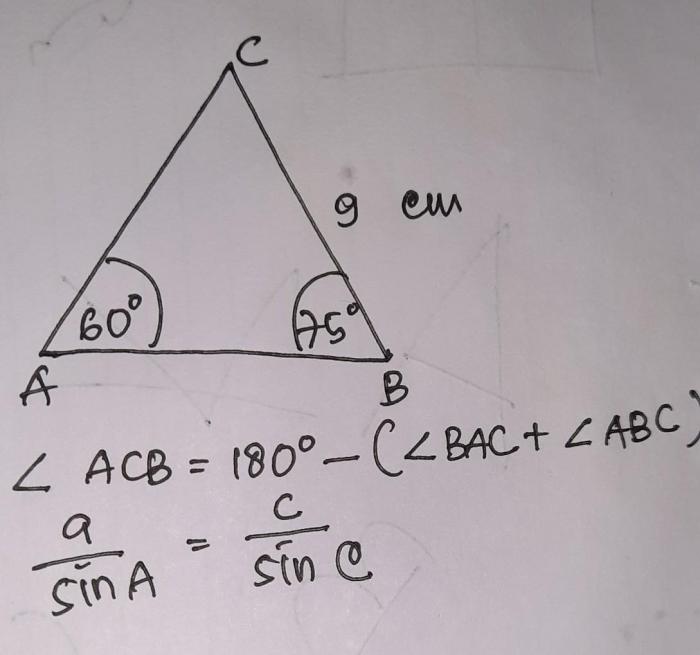
Segitiga ABC adalah segitiga yang memiliki tiga sisi, yaitu AB, BC, dan AC. Keliling segitiga adalah jumlah panjang ketiga sisinya, sedangkan luasnya adalah setengah dari hasil perkalian panjang alas dan tinggi.

Keliling Segitiga ABC

Untuk menghitung keliling segitiga ABC, kita perlu mengetahui panjang ketiga sisinya. Rumus keliling segitiga adalah:

k = AB + BC + AC

di mana:

• k adalah keliling segitiga
• AB adalah panjang sisi AB
• BC adalah panjang sisi BC
• AC adalah panjang sisi AC

Luas Segitiga ABC

Untuk menghitung luas segitiga ABC, kita perlu mengetahui panjang alas dan tingginya. Alas segitiga adalah salah satu sisi segitiga, sedangkan tinggi segitiga adalah jarak dari alas ke titik puncak segitiga. Rumus luas segitiga adalah:

L = 1/2

• alas
• tinggi

di mana:

• L adalah luas segitiga
• alas adalah panjang alas segitiga
• tinggi adalah tinggi segitiga

Contoh Perhitungan

Misalkan kita memiliki segitiga ABC dengan panjang sisi AB = 5 cm, BC = 7 cm, dan AC = 8 cm. Maka keliling dan luas segitiga ABC dapat dihitung sebagai berikut:

Keliling

k = AB + BC + ACk = 5 cm + 7 cm + 8 cmk = 20 cm

Luas

Misalkan alas segitiga adalah sisi AB dan tinggi segitiga adalah jarak dari sisi AB ke titik puncak C. Tinggi segitiga dapat dihitung menggunakan teorema Pythagoras:

tinggi = √(AC²

AB²)

tinggi = √(8²

5²)

tinggi = √(64

25)

tinggi = √39tinggi ≈ 6,24 cm

Maka luas segitiga ABC adalah:

L = 1/2

• alas
• tinggi

L = 1/2

• 5 cm
• 6,24 cm

L = 15,6 cm²

Aplikasi Segitiga ABC

Segitiga ABC adalah salah satu bentuk geometri paling dasar dan serbaguna. Bentuk ini memiliki berbagai aplikasi di berbagai bidang, termasuk geometri, fisika, dan kehidupan sehari-hari.

Geometri

• Menghitung luas dan keliling
• Menentukan sifat segitiga (siku-siku, sama sisi, dll.)
• Membangun bentuk geometri yang lebih kompleks

Fisika

• Menghitung gaya dan tekanan
• Memodelkan gerak benda
• Menganalisis kesetimbangan dan stabilitas

Kehidupan Sehari-hari

• Arsitektur: Mendesain atap, dinding, dan struktur lainnya
• Teknik: Mendesain jembatan, bangunan, dan mesin
• Seni: Membuat lukisan, patung, dan desain grafis

Contoh spesifik penggunaan segitiga ABC dalam praktik meliputi:

• Perhitungan luas tanah untuk perencanaan pembangunan
• Perhitungan gaya pada rangka jembatan
• Desain atap berbentuk segitiga untuk bangunan

Sifat Khusus Segitiga ABC

Segitiga ABC dapat diklasifikasikan menjadi beberapa jenis khusus berdasarkan sifat-sifat uniknya. Jenis-jenis segitiga khusus tersebut meliputi:

Segitiga Siku-Siku

Segitiga siku-siku memiliki satu sudut siku-siku (90 derajat). Sifat-sifat khusus segitiga siku-siku meliputi:

• Sisi terpanjang (hipotenusa) berada di hadapan sudut siku-siku.
• Kuadrat panjang sisi terpanjang sama dengan jumlah kuadrat panjang kedua sisi lainnya (Teorema Pythagoras).

Segitiga Sama Kaki

Segitiga sama kaki memiliki dua sisi yang sama panjang. Sifat-sifat khusus segitiga sama kaki meliputi:

• Sudut yang berhadapan dengan sisi yang sama panjang adalah sama besar.
• Tinggi dari titik sudut ke sisi dasar membagi sisi dasar menjadi dua bagian yang sama panjang.

Segitiga Sama Sisi

Segitiga sama sisi memiliki tiga sisi yang sama panjang. Sifat-sifat khusus segitiga sama sisi meliputi:

• Semua sudut sama besar (60 derajat).
• Tinggi dari titik sudut mana pun membagi sisi yang berhadapan menjadi dua bagian yang sama panjang.

Pembuktian Rumus dan Sifat Segitiga ABC

Dalam geometri, terdapat beberapa rumus dan sifat penting yang terkait dengan segitiga ABC. Pembuktian rumus dan sifat-sifat ini sangat penting untuk memahami sifat segitiga dan menerapkannya dalam berbagai aplikasi.

Pembuktian Rumus Keliling Segitiga

Keliling segitiga ABC adalah jumlah panjang ketiga sisinya, yang dinyatakan dengan rumus K = a + b + c. Pembuktian rumus ini dapat dilakukan dengan menggunakan aksioma jarak terpendek. Aksioma ini menyatakan bahwa jarak terpendek antara dua titik adalah garis lurus.

Oleh karena itu, keliling segitiga adalah jumlah panjang garis lurus yang menghubungkan ketiga titik sudut segitiga.

Pembuktian Rumus Luas Segitiga

Luas segitiga ABC adalah setengah dari hasil kali alas dan tinggi segitiga, yang dinyatakan dengan rumus L = (1/2) – a – t. Pembuktian rumus ini dapat dilakukan dengan menggunakan konsep segitiga yang mirip. Dua segitiga dikatakan mirip jika sudut-sudutnya sama.

Dalam hal ini, segitiga ABC dapat dibagi menjadi dua segitiga yang mirip dengan alas dan tinggi yang sama.

Pembahasan Metode Pembuktian Sifat Segitiga

Pembuktian sifat-sifat segitiga biasanya dilakukan dengan menggunakan beberapa metode, antara lain:

• Aksioma dan Teorema: Sifat-sifat segitiga dapat dibuktikan dengan menggunakan aksioma dan teorema yang telah ditetapkan sebelumnya.
• Konstruksi Geometris: Sifat-sifat segitiga dapat dibuktikan dengan melakukan konstruksi geometris, seperti menggambar garis bantu atau membuat segitiga baru.
• Persamaan dan Pertidaksamaan: Sifat-sifat segitiga dapat dibuktikan dengan menggunakan persamaan dan pertidaksamaan, seperti persamaan sudut atau pertidaksamaan panjang sisi.

Ringkasan Penutup

Memahami sifat, rumus, dan aplikasi segitiga ABC sangat penting untuk penguasaan konsep geometri yang komprehensif. Segitiga ini memberikan dasar untuk eksplorasi bentuk geometris yang lebih kompleks dan memiliki peran penting dalam berbagai bidang seperti fisika, teknik, dan seni. Dengan menguasai topik ini, kita dapat menghargai keindahan dan kekuatan matematika dalam menggambarkan dunia di sekitar kita.

Pertanyaan yang Sering Diajukan

Apa itu segitiga ABC?

Segitiga ABC adalah segitiga yang memiliki tiga sisi dan tiga sudut, dengan titik sudut yang diberi label A, B, dan C.

Apa rumus untuk menghitung keliling segitiga ABC?

Keliling = a + b + c, di mana a, b, dan c adalah panjang sisi segitiga.

Apa aplikasi segitiga ABC dalam kehidupan sehari-hari?

Segitiga ABC digunakan dalam arsitektur, desain, navigasi, dan banyak lagi.