Distribusi normal, juga dikenal sebagai distribusi Gaussian, merupakan distribusi probabilitas yang memainkan peran penting dalam berbagai bidang ilmu pengetahuan dan kehidupan nyata. Karakteristiknya yang khas dan kemudahan dalam penyelesaian soal menjadikannya alat yang ampuh untuk analisis data dan pengambilan keputusan.

Dalam uraian ini, kita akan mendefinisikan distribusi normal, mengeksplorasi karakteristiknya, dan memberikan contoh soal untuk memperdalam pemahaman. Selain itu, kita juga akan membahas langkah-langkah untuk menyelesaikan soal distribusi normal dan penerapannya yang luas dalam berbagai bidang.

Pengertian Distribusi Normal

Distribusi normal, juga dikenal sebagai distribusi Gaussian atau distribusi lonceng, adalah distribusi probabilitas berkelanjutan yang menggambarkan data yang terdistribusi secara simetris di sekitar nilai rata-rata.

Distribusi ini dicirikan oleh kurva berbentuk lonceng yang khas, dengan titik puncak pada rata-rata dan ekor yang meruncing ke arah tak terhingga di kedua sisi.

Karakteristik Khas Distribusi Normal

• Simetri: Distribusi normal simetris di sekitar nilai rata-ratanya.
• Bentuk Lonceng: Kurva berbentuk lonceng dengan titik puncak pada rata-rata dan ekor yang meruncing ke arah tak terhingga di kedua sisi.
• Titik Infleksi: Distribusi normal memiliki dua titik infleksi pada jarak yang sama dari rata-rata, di mana kurva berubah dari cekung ke cembung.
• Area di Bawah Kurva: Luas di bawah kurva distribusi normal sama dengan 1.
• Kemiringan: Distribusi normal lebih curam di dekat rata-rata dan lebih datar di ekor.

Contoh Soal Distribusi Normal

Distribusi normal adalah distribusi probabilitas yang sangat penting dalam statistik. Ini digunakan untuk memodelkan banyak fenomena alam dan sosial.

Contoh Soal

Berikut adalah beberapa contoh soal yang melibatkan distribusi normal:

• Tinggi rata-rata siswa di sebuah sekolah adalah 170 cm dengan simpangan baku 5 cm. Berapakah probabilitas siswa yang dipilih secara acak memiliki tinggi antara 165 cm dan 175 cm?
• Nilai ujian matematika suatu kelas berdistribusi normal dengan rata-rata 75 dan simpangan baku 10. Berapakah persentase siswa yang mendapat nilai di atas 90?
• Waktu tunggu di sebuah bank berdistribusi normal dengan rata-rata 10 menit dan simpangan baku 2 menit. Berapakah probabilitas seseorang harus menunggu lebih dari 15 menit?

Cara Menyelesaikan Soal Distribusi Normal

Distribusi normal adalah distribusi probabilitas yang banyak digunakan dalam statistik. Untuk menyelesaikan soal distribusi normal, terdapat beberapa langkah yang dapat diikuti:

1. Identifikasi parameter distribusi normal, yaitu mean (μ) dan standar deviasi (σ).
2. Standarisasi variabel acak X menggunakan rumus Z = (X
   

   μ) / σ.

3. Cari probabilitas atau nilai kritis menggunakan tabel distribusi normal atau kalkulator statistik.
4. Interpretasikan hasil yang diperoleh dalam konteks soal.

Contoh Penggunaan Rumus dan Tabel Distribusi Normal

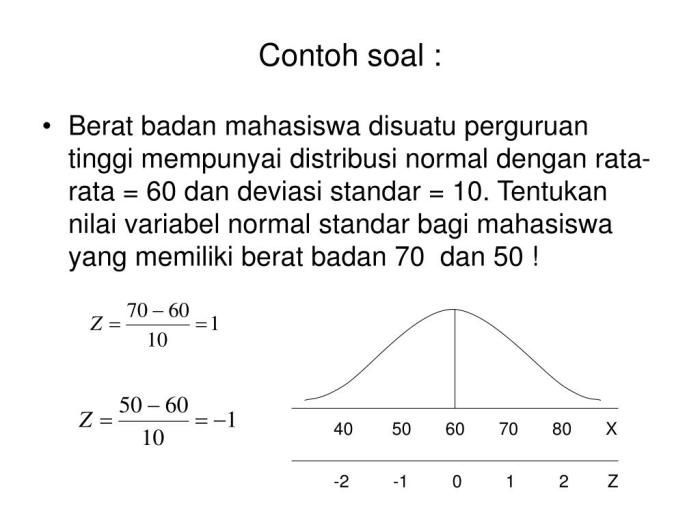
Misalkan berat badan populasi siswa laki-laki berdistribusi normal dengan mean 70 kg dan standar deviasi 5 kg.

Berapakah probabilitas seorang siswa laki-laki memiliki berat badan lebih dari 80 kg?Langkah 1: Identifikasi parameterμ = 70 kg, σ = 5 kgLangkah 2: StandarisasiZ = (80

70) / 5 = 2

Langkah 3: Cari probabilitasMenggunakan tabel distribusi normal, diperoleh P(Z > 2) = 0,0228Langkah 4: InterpretasiJadi, probabilitas seorang siswa laki-laki memiliki berat badan lebih dari 80 kg adalah 0,0228 atau sekitar 2,28%.

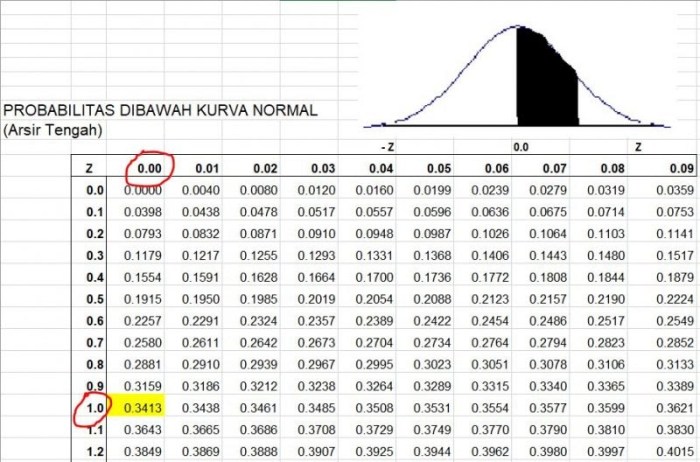
Prosedur Menggunakan Tabel Distribusi Normal

Tabel distribusi normal adalah alat statistik yang digunakan untuk mencari probabilitas nilai dalam distribusi normal. Untuk menggunakan tabel ini, ikuti langkah-langkah berikut:

Mencari Nilai Probabilitas

• Temukan nilai baku (z-score) untuk nilai yang diinginkan menggunakan rumus z = (x
  – μ) / σ, di mana x adalah nilai yang diinginkan, μ adalah mean distribusi, dan σ adalah simpangan baku distribusi.
• Cari baris pada tabel yang sesuai dengan nilai z bulat terdekat.
• Cari kolom pada tabel yang sesuai dengan desimal nilai z.
• Nilai pada titik temu baris dan kolom tersebut adalah probabilitas bahwa nilai yang diinginkan terjadi dalam distribusi normal.

Mencari Nilai Baku

• Temukan probabilitas yang diinginkan pada tabel.
• Cari baris dan kolom pada tabel yang sesuai dengan probabilitas tersebut.
• Nilai z bulat terdekat yang tertera pada baris tersebut adalah nilai baku yang sesuai dengan probabilitas yang diinginkan.

Aplikasi Distribusi Normal dalam Kehidupan Nyata

Distribusi normal, juga dikenal sebagai distribusi Gaussian, adalah salah satu distribusi probabilitas yang paling penting dan banyak digunakan dalam berbagai bidang. Bentuknya yang berbentuk lonceng simetris memungkinkan kita untuk memodelkan banyak fenomena alam dan buatan manusia.

Statistik

Dalam statistik, distribusi normal digunakan untuk menganalisis data dan membuat inferensi tentang populasi. Misalnya, kita dapat menggunakan distribusi normal untuk:

• Memperkirakan rata-rata populasi berdasarkan sampel.
• Menguji hipotesis tentang rata-rata atau varians populasi.
• Membuat interval kepercayaan untuk rata-rata atau varians populasi.

Keuangan

Dalam keuangan, distribusi normal digunakan untuk memodelkan pengembalian investasi dan harga aset. Misalnya, kita dapat menggunakan distribusi normal untuk:

• Memperkirakan risiko dan pengembalian investasi.
• Mengevaluasi kinerja portofolio investasi.
• Membuat keputusan tentang alokasi aset.

Ilmu Sosial

Dalam ilmu sosial, distribusi normal digunakan untuk menganalisis data dan menguji hipotesis tentang perilaku manusia. Misalnya, kita dapat menggunakan distribusi normal untuk:

• Membandingkan rata-rata skor tes antara dua kelompok.
• Menguji hipotesis tentang hubungan antara dua variabel.
• Membuat prediksi tentang perilaku manusia berdasarkan data historis.

Penutup

Distribusi normal adalah alat yang berharga untuk memodelkan fenomena yang beragam dalam kehidupan nyata. Pemahaman yang mendalam tentang konsep dan penerapannya sangat penting bagi individu yang bekerja dengan data dan statistik. Dengan menguasai teknik penyelesaian soal distribusi normal, kita dapat memperoleh wawasan berharga dari data dan membuat keputusan yang tepat berdasarkan informasi.

Pertanyaan Umum yang Sering Muncul

Apa ciri-ciri utama dari distribusi normal?

Distribusi normal simetris, berbentuk lonceng, dan memiliki mean, median, dan modus yang sama.

Bagaimana cara menyelesaikan soal distribusi normal?

Soal distribusi normal dapat diselesaikan dengan menggunakan rumus standar deviasi atau dengan merujuk pada tabel distribusi normal.

Di bidang apa saja distribusi normal digunakan?

Distribusi normal banyak digunakan dalam statistik, keuangan, ilmu sosial, dan bidang lainnya untuk menganalisis data dan membuat prediksi.