Dalam dunia matematika, faktorisasi prima memainkan peran penting dalam memahami komposisi numerik. Dengan membagi suatu bilangan menjadi faktor-faktor primanya, kita mengungkap struktur dasarnya, yang mengarah pada wawasan tentang sifat-sifatnya.
Salah satu bilangan yang menarik untuk dijelajahi adalah 140. Dalam artikel ini, kita akan menyelami proses faktorisasi prima dari 140, menyingkap pentingnya teknik ini dalam berbagai bidang.
Pemahaman Faktorisasi Prima
Faktorisasi prima adalah proses penguraian suatu bilangan menjadi perkalian faktor-faktor primanya. Faktor prima adalah bilangan prima yang membagi habis suatu bilangan tanpa menghasilkan sisa.
Dengan kata lain, faktorisasi prima adalah bentuk penguraian suatu bilangan menjadi bentuk paling sederhana, di mana bilangan tersebut tidak dapat dibagi lagi oleh bilangan bulat selain dirinya sendiri dan 1.
Langkah-Langkah Faktorisasi Prima
- Bagilah bilangan tersebut dengan bilangan prima terkecil yang membagi habisnya.
- Lanjutkan membagi hasil bagi dengan bilangan prima berikutnya yang membagi habisnya.
- Ulangi langkah 2 hingga hasil bagi tidak dapat dibagi lagi oleh bilangan prima.
- Hasil akhir adalah perkalian semua bilangan prima yang diperoleh pada setiap pembagian.
Langkah-Langkah Faktorisasi Prima
Faktorisasi prima adalah proses penguraian suatu bilangan menjadi faktor-faktor primanya, yaitu bilangan-bilangan prima yang mengalikannya. Berikut adalah langkah-langkah untuk memfaktorkan bilangan menjadi faktor primanya:
Temukan Faktor Prima Terkecil
- Bagi bilangan dengan bilangan prima terkecil yang habis membaginya (2, 3, 5, 7, 11, …).
- Jika tidak habis, lanjutkan ke bilangan prima berikutnya.
Bagi Berulang Kali
- Setelah menemukan faktor prima terkecil, bagi bilangan dengan faktor tersebut berulang kali.
- Ulangi langkah ini hingga bilangan tidak dapat dibagi lagi dengan faktor prima yang sama.
Cari Faktor Prima Berikutnya
- Setelah semua faktor prima untuk faktor yang baru ditemukan habis dibagi, lanjutkan mencari faktor prima berikutnya dengan bilangan prima yang lebih besar dari faktor sebelumnya.
- Ulangi langkah 2 dan 3 hingga bilangan tersebut menjadi 1.
Tuliskan Faktor Prima
- Faktor-faktor prima yang ditemukan pada setiap langkah merupakan faktor prima dari bilangan awal.
- Faktor-faktor tersebut dapat dituliskan dalam bentuk perkalian untuk mendapatkan bilangan awal.
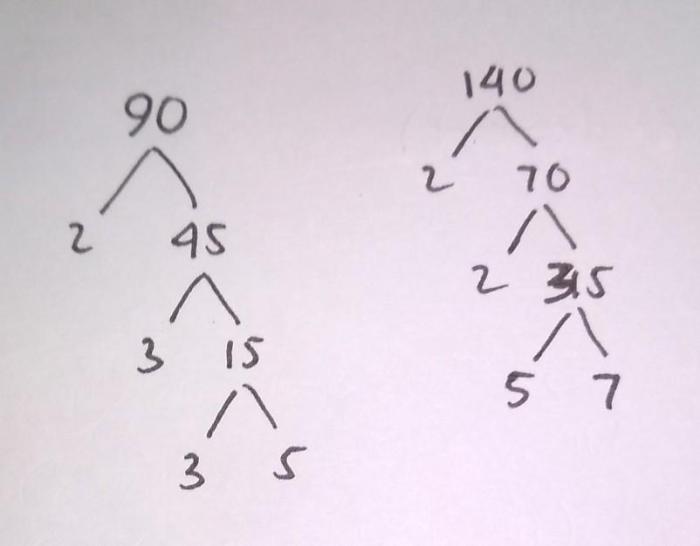
Faktorisasi Prima 140
Faktorisasi prima adalah proses menguraikan suatu bilangan menjadi faktor-faktor primanya, yaitu bilangan yang hanya habis dibagi oleh 1 dan bilangan itu sendiri. Dalam kasus ini, kita akan memfaktorkan bilangan 140 menjadi faktor primanya.
Langkah-langkah Faktorisasi Prima
- Bagilah bilangan dengan bilangan prima terkecil yang habis membaginya. Dalam hal ini, 140 habis dibagi 2.
- Lanjutkan membagi hasil bagi dengan bilangan prima berikutnya yang habis membaginya. 70 habis dibagi 2.
- Ulangi langkah 2 hingga hasil bagi tidak dapat dibagi lagi oleh bilangan prima apa pun. 35 tidak dapat dibagi lagi oleh bilangan prima apa pun selain 5 dan 7.
Hasil Faktorisasi Prima
Dari langkah-langkah di atas, kita memperoleh faktorisasi prima 140 sebagai berikut:“`
= 2 x 2 x 5 x 7
“`
Pentingnya Faktorisasi Prima
Faktorisasi prima adalah proses penguraian suatu bilangan menjadi faktor-faktor primanya. Faktorisasi prima memiliki peran penting dalam berbagai bidang, termasuk matematika, komputasi, dan kriptografi.
Dalam matematika, faktorisasi prima digunakan untuk menentukan sifat suatu bilangan. Misalnya, suatu bilangan prima jika hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Faktorisasi prima juga digunakan untuk menyelesaikan persamaan dan mencari solusi bilangan bulat.
Contoh Penggunaan Faktorisasi Prima
- Kriptografi: Faktorisasi prima digunakan dalam algoritma kriptografi, seperti RSA, untuk mengenkripsi dan mendekripsi pesan.
- Pengoptimalan: Faktorisasi prima digunakan dalam algoritma pengoptimalan untuk menemukan solusi optimal untuk masalah tertentu.
- Komputasi Paralel: Faktorisasi prima digunakan untuk mendistribusikan tugas komputasi ke beberapa prosesor, meningkatkan kecepatan komputasi.
Contoh Tambahan
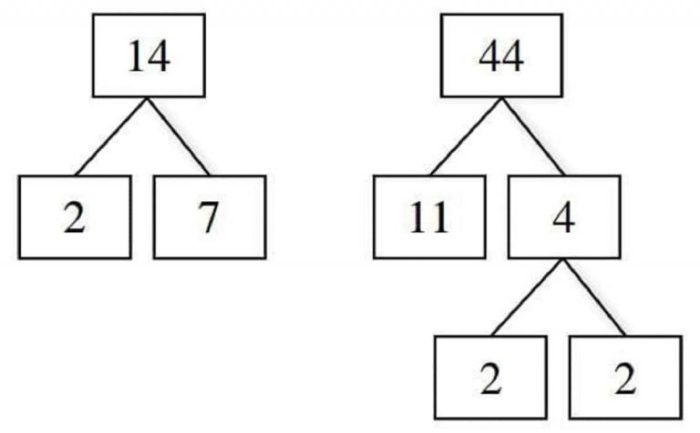
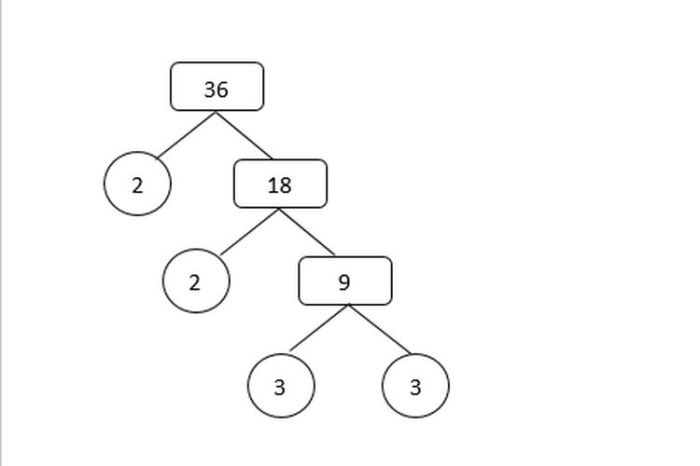
Untuk memperkuat pemahaman, berikut adalah beberapa contoh tambahan bilangan dan faktorisasi primanya:
Dengan menerapkan proses yang sama seperti sebelumnya, kita dapat menemukan faktorisasi prima dari bilangan-bilangan ini.
Tabel Faktorisasi Prima
| Bilangan | Faktorisasi Prima | Langkah-langkah |
|---|---|---|
| 120 | 23 × 3 × 5 |
|
| 210 | 2 × 3 × 5 × 7 |
|
| 360 | 23 × 32 × 5 |
|
Cara Alternatif untuk Memfaktorkan
Selain metode dasar, terdapat cara alternatif untuk memfaktorkan bilangan, seperti menggunakan pohon faktor.
Pohon Faktor
Pohon faktor adalah representasi hierarkis dari faktor-faktor suatu bilangan. Setiap node dalam pohon mewakili faktor dari bilangan yang bersangkutan, dan anak-anak dari suatu node mewakili faktor dari faktor tersebut. Pohon faktor dapat membantu memvisualisasikan faktorisasi prima suatu bilangan.
Kelebihan:
- Menyediakan representasi visual faktorisasi prima.
- Membantu mengidentifikasi faktor-faktor yang umum bagi beberapa bilangan.
Kekurangan:
- Tidak efisien untuk bilangan besar.
- Tidak memberikan faktorisasi unik untuk beberapa bilangan.
Kesulitan dan Strategi

Memfaktorkan bilangan prima bisa menjadi tugas yang menantang, terutama untuk bilangan yang besar. Kesulitan umum yang dihadapi antara lain:
- Mengidentifikasi faktor-faktor prima yang besar.
- Memastikan bahwa semua faktor prima telah ditemukan.
Untuk mengatasi kesulitan ini, beberapa strategi dapat digunakan:
Strategi 1
- Gunakan Kalkulator atau Aplikasi: Ada banyak kalkulator dan aplikasi online yang dapat memfaktorkan bilangan dengan cepat dan akurat.
- Metode Pohon Faktor: Metode ini melibatkan pembuatan pohon yang mewakili semua kemungkinan faktor dari suatu bilangan. Faktor yang tidak menghasilkan pohon yang valid dapat dihilangkan.
- Metode Pembagian Berulang: Metode ini melibatkan pembagian bilangan berulang kali dengan bilangan prima terkecil yang mungkin, hingga bilangan tersebut tidak dapat dibagi lagi.
Terakhir
Faktorisasi prima dari 140 tidak hanya memberikan pemahaman tentang bilangan itu sendiri, tetapi juga menyoroti kekuatan faktorisasi prima sebagai alat untuk mengungkap sifat-sifat numerik yang mendasar. Dari matematika hingga komputasi, teknik ini terus memainkan peran penting dalam memecahkan masalah dan memajukan pengetahuan kita tentang angka.
Pertanyaan Umum (FAQ)
Apa pentingnya faktorisasi prima?
Faktorisasi prima memungkinkan kita untuk memahami struktur dasar bilangan, mengidentifikasi pola, dan memecahkan masalah matematika yang kompleks.
Bagaimana cara memfaktorkan bilangan selain 140?
Proses faktorisasi prima sama untuk semua bilangan. Bagi bilangan secara berulang dengan bilangan prima terkecil yang dapat habis dibagi, dan lanjutkan proses ini hingga diperoleh faktor prima.
Apa saja kesulitan yang dihadapi dalam faktorisasi prima?
Kesulitan umum adalah menemukan faktor prima untuk bilangan yang sangat besar, yang memerlukan teknik khusus seperti metode pohon faktor.